1.2 Row reduction and echelon forms (行化简与阶梯式矩阵)

本文为《Linear algebra and its applications》的读书笔记

This section refines the method of Section 1.1 into a row reduction algorithm (commonly called Gaussian elimination 高斯消去法) that will enable us to analyze any system of linear equations

In the definitions that follow, a nonzero row or column in a matrix means a row or column that contains at least one nonzero entry; a leading entry (先导元素) of a row refers to the leftmost nonzero entry (in a nonzero row).

Definition

A rectangular matrix is in echelon form (阶梯形) (or row echelon form(行阶梯形)) if it has the following three properties:

1. All nonzero rows are above any rows of all zeros. 每一非零行都在每一零行之上
2. Each leading entry of a row is in a column to the right of the leading entry of
   the row above it. 某一行的先导元素所在的列位于前一行先导元素的右边
3. All entries in a column below a leading entry are zeros. 某一先导元素所在列下方元素都是0

Property 3 is a simple consequence of property 2 (性质3其实是性质2的推论), but we include it for emphasis.

If a matrix in echelon form satisfies the following additional conditions, then it is in reduced echelon form (简化阶梯形) (or reduced row echelon form(简化行阶梯形)):

1. The leading entry in each nonzero row is 1.
2. Each leading 1 is the only nonzero entry in its column.

An echelon matrix (respectively, reduced echelon matrix) is one that is in echelon form (respectively, reduced echelon form).

The “triangular” matrices, such as

are in echelon form. In fact, the second matrix is in reduced echelon form.

EXAMPLE 1
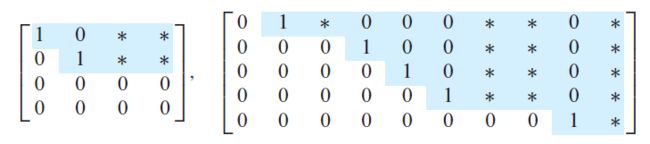
The following matrices are in echelon form. The leading entries may have any nonzero value; the starred entries (*) may have any value (including zero).

The following matrices are in reduced echelon form

Uniqueness of the Reduced Echelon Form

Any nonzero matrix may be row reduced into more than one matrix in echelon form, using different sequences of row operations. However, the reduced echelon form one obtains from a matrix is unique (一个矩阵只能化成唯一的简化阶梯形矩阵).

(简化阶梯形矩阵的唯一性：每个矩阵行等价于唯一的简化阶梯形矩阵)

If a matrix A is row equivalent to an echelon matrix U, we call U an echelon form (or row echelon form) of A (U为A的阶梯形); if U is in reduced echelon form, we call U the reduced echelon form of A (U为A的简化阶梯形).

Most matrix programs and calculators with matrix capabilities use the abbreviation RREF for reduced (row) echelon form. Some use REF for (row) echelon form.

Pivot Positions 主元位置

When row operations on a matrix produce an echelon form, further row operations to obtain the reduced echelon form do not change the positions of the leading entries. Since the reduced echelon form is unique, the leading entries are always in the same positions in any echelon form obtained from a given matrix (给定矩阵化为任一阶梯形时，先导元素总在相同位置上).

DEFINITION：
A pivot position (主元位置) in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column (主元列) is a column of A that contains a pivot position.

EXAMPLE 2

• Row reduce the matrix A below to echelon form, and locate the pivot columns of A.
  
  
  

A pivot (主元) is a nonzero number in a pivot position that is used as needed to create zeros via row operations.

Notice that pivots are not the same as the actual elements of A in the pivot positions

The Row Reduction Algorithm 行化简算法

EXAMPLE 3
Apply elementary row operations to transform the following matrix first into echelon form and then into reduced echelon form:

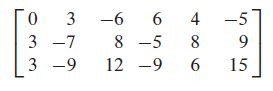
SOLUTION
STEP 1
Begin with the leftmost nonzero column. This is a pivot column.

STEP 2
Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position.

a computer program usually selects as a pivot the entry in a column having the largest absolute value. This strategy, called partial pivoting(部分主元法), is used because it reduces roundoff errors in the calculations.

STEP 3
Use row replacement operations to create zeros in all positions below the pivot.

STEP 4
Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1–3 to the submatrix that remains. Repeat the process until there are no more nonzero rows to modify.
With row 1 covered, step 1 shows that column 2 is the next pivot column


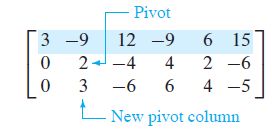
When we cover the row containing the second pivot position for step 4, we are left with a new submatrix having only one row:

Steps 1–3 require no work for this submatrix, and we have reached an echelon form of the full matrix.
STEP 5 (进一步化为简化阶梯形)
Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by a scaling operation




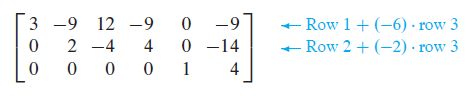
This is the reduced echelon form of the original matrix.

Solutions of Linear Systems

Suppose, for example, that the augmented matrix of a linear system has been changed into the equivalent reduced echelon form


The variables $x_1$ and $x_2$ corresponding to pivot columns in the matrix are called basic variables (基本变量). The other variable, $x_3$, is called a free variable (自由变量).

Whenever a system is consistent, the solution set can be described explicitly by solving the reduced system of equations for the basic variables in terms of the free variables. This operation is possible because the reduced echelon form places each basic variable in one and only one equation.

In (4), solve the first equation for $x_1$ and the second for $x_2$.

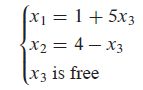
Each different choice of $x_3$ determines a (different) solution of the system, and every solution of the system is determined by a choice of $x_3$.

上面的联立方程组也称为通解(the general solution)

EXAMPLE 4
Find the general solution of the linear system whose augmented matrix has been reduced to

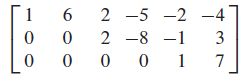
SOLUTION
The matrix is in echelon form, but we want the reduced echelon form before solving for the basic variables.


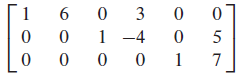
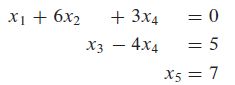
The pivot columns of the matrix are 1, 3, and 5, so the basic variables are $x_1$, $x_3$, and $x_5$. The remaining variables, $x_2$ and $x_4$, must be free. Solve for the basic variables to obtain the general solution:

应用：
Suppose experimental data are represented by a set of points in the plane. An interpolating polynomial (插值多项式) for the data is a polynomial whose graph passes through every point. In scientific work, such a polynomial can be used, for example, to estimate values between the known data points.
One method for finding an interpolating polynomial is to solve a system of linear equations.
e.g.Find the interpolating polynomial $p(t)=a_0+a_{1}t+a_2{t}^2$ for the data (1, 12), (2, 15), (3, 16)：

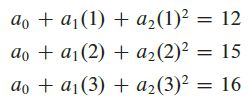
Parametric Descriptions of Solution Sets 解集的参数表示

parametric descriptions of solution sets in which the free variables act as parameters：

Whenever a system is consistent and has free variables, the solution set has many parametric descriptions. However, to be consistent, we make the (arbitrary) convention of always using the free variables as the parameters for describing a solution set.

Whenever a system is inconsistent, the solution set has no parametric representation.

Back-Substitution 回代

下面的线性方程组是阶梯形式，但不是简化阶梯形式：

A computer program would solve this system by back-substitution, rather than by computing the reduced echelon form.

程序先解第3个方程，用$x_5$表示$x_4$，并将此表达式代入第2个方程，解出$x_2$，最后把$x_2$和$x_4$的表达式代入第1个方程接出$x_1$

Existence and Uniqueness Questions

Although a nonreduced echelon form is a poor tool for solving a system, this form is just the right device for answering two fundamental questions posed in Section 1.1.

EXAMPLE 5
Determine the existence and uniqueness of the solutions to the system

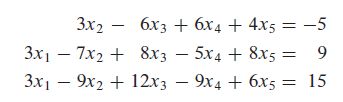
SOLUTION

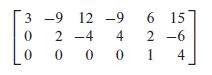
The basic variables are $x_1$, $x_2$, and $x_5$; the free variables are $x_3$and $x_4$. There is no equation such as 0 = 1 that would indicate an inconsistent system. The existence of a solution is already clear. Also, the solution is not unique because there are free variables. (Each different choice of $x_3$ and $x_4$ determines a different solution)

如果线性方程组是相容的，则解释唯一的当且仅当系数矩阵的每一列都是主元列。否则，方程组有无穷多解
这也解释了为什么方程个数少于未知数个数时(欠定方程组)，若相容，则一定有无穷多解

USING ROW REDUCTION TO SOLVE A LINEAR SYSTEM

1. Write the augmented matrix of the system.
2. Use the row reduction algorithm to obtain an equivalent augmented matrix in echelon form. Decide whether the system is consistent. If there is no solution, stop; otherwise, go to the next step.
3. Continue row reduction to obtain the reduced echelon form.
4. Write the system of equations corresponding to the matrix obtained in step 3.
5. Rewrite each nonzero equation from step 4 so that its one basic variable is expressed in terms of any free variables appearing in the equation.