机器学习 | 分类评估指标

相关文章：

机器学习 | 目录

机器学习 | 回归评估指标

1. 分类评估指标

评估指标（Evaluation Matrix）：在建立模型后，我们想要知道它的性能如何，因此我们将通过一系列指标来判断一个模型的好坏。

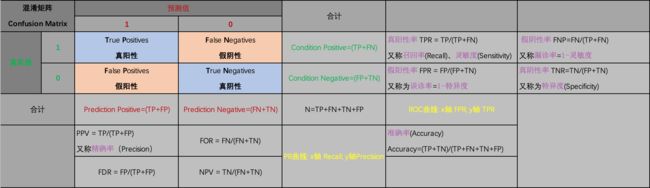
1.1 混淆矩阵 Confusion Matrix

混淆矩阵也称误差矩阵，是表示精度评价的一种标准格式，用$n$行$n$列的矩阵形式来表示。在人工智能中，混淆矩阵（Confusion Matrix）是误差可视化工具，特别用于监督学习；在无监督学习一般叫做匹配矩阵。

混淆矩阵

1. 每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目

2. 每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数目

3. 每一行之和表示该类别的真实样本数量，每一列之和表示被预测为该类别的样本数量

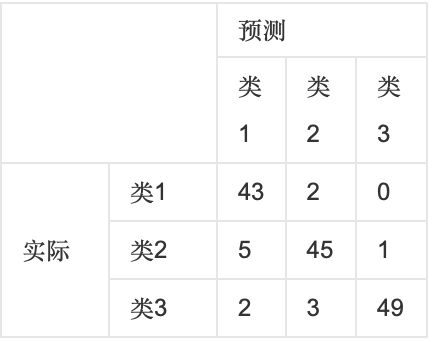
如下图，第一行第一列中的43表示有43个实际归属第一类的实例被预测为第一类，同理，第一行第二列的2表示有2个实际归属为第一类的实例被错误预测为第二类。

1.1.1 scikit-learn 混淆矩阵函数接口

skearn.metrics.confusion_matrix(
    y_true,   # array, Gound true (correct) target values
    y_pred,  # array, Estimated targets as returned by a classifier
    labels=None,  # array, List of labels to index the matrix.
    sample_weight=None  # array-like of shape = [n_samples], Optional sample weights
)

参数设置：

y_true : array, shape = [n_samples]

Ground truth (correct) target values.

y_pred : array, shape = [n_samples]

Estimated targets as returned by a classifier.

labels : array, shape = [n_classes], optional

List of labels to index the matrix. This may be used to reorder or select a subset of labels. If none is given, those that appear at least once in y_true or y_pred are used in sorted order.

sample_weight : array-like of shape = [n_samples], optional

Sample weights.

返回值：

array, shape = [n_classes, n_classes]

Confusion matrix

在 scikit-learn 中, 计算混淆矩阵用来评估分类的准确度。

按照定义, 混淆矩阵$C$中的元素$C_{i,j}$为真实值的为组$i$, 而预测为组$j$的观测数(the number of observations)。

对于二分类任务, 预测结果中：

• 真阳数（True Positives, TP）为$C_{1,1}$
• 真阴数（True Negatives, TN）为$C_{0,0}$
• 假阳数（False Posiives, FN）为$C_{1,0}$
• 假阴数（False Negatives, FN）为$C_{1,0}$

如果 labels 为 None, scikit-learn 会把在出现在 y_true 或 y_pred 中的所有值添加到标记列表 labels 中, 并排好序。^[1]

sklearn.metrics.confusion_matrix 官方文档

1.2 真阳性TP、假阳性FP、真阴性TN、假阴性FN

对于二分类任务：

• 真阳性（True Positives, TP）为真实值为1，预测值为1，即正确预测出的正样本个数
• 真阴性（True Negatives, TN）为真实值为0，预测值为0，即正确预测出的负样本个数
• 假阳性（False Posiives, FP）为真实值为0，预测值为1，即错误预测出的正样本个数（即数理统计的第一类错误）
• 假阴性（False Negatives, FN）为真实值为1，预测值为0，即错误预测出的负样本个数（即数理统计的第二类错误）

概括地来说：

• 当预测值为1时，体现为阳性；当预测值为0时，体现为阴性
• 当预测值与真实值相符时，为真；当预测值与真实值相反时，为假

阳性、阴性由来：这两个概念是从医学上引进的，一般来说，阳性（+）是表示疾病或体内生理的变化有一定的结果。相反，化验单或报告单上的阴性（－），则多数基本上否定或排除某种病变的可能性。

---

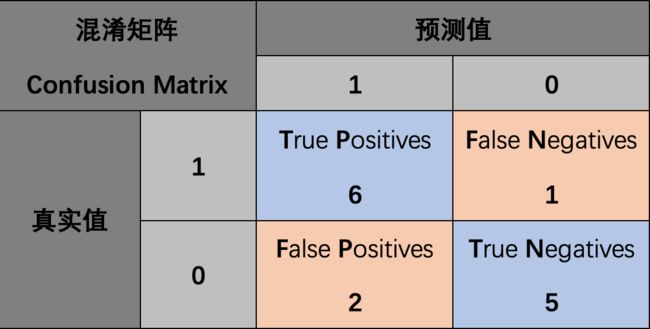
例1. 计算真阳性、假阳性、真阴性、假阴性：

如图所示，蓝色为阳性，红色为阴性；我们训练的模型是一条直线来划分这个区域，阳性区域在上，阴性区域在下。

因此直线上方的点预测值为1，其中6个蓝点的真实值为1，2个两红点的真实值为0，因此真阳性个数为6，假阳性个数为2；直线下方的点预测值为0，其中5个红点真实值为0，1个蓝点真实值为1，因此真阴性个数为5，假阴性个数为1。最终混淆矩阵如下所示：

1.2.1 衍生评估指标

由TP、FP、TN、FN四个指标，可以进一步衍生出其他三个常用的评价分类器性能的指标：

1. 准确率 Accuracy

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}\text{\hspace{1em}(1)}$$

2. 精确率 Precision

$$Precision=\frac{TP}{TP+FP}\text{\hspace{1em}(2)}$$

3. 召回率 Recall

$$Recall=\frac{TP}{TP+FN}\text{\hspace{1em}(3)}$$

我们将会在后面对这些指标进行说明。

这是所有的衍生指标：

1.3 准确率 Accuracy

准确率（Accuracy）：分类器预测出的正样本中，真实正样本的比例，计算公式如下：

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}\text{\hspace{1em}(4)}$$

---

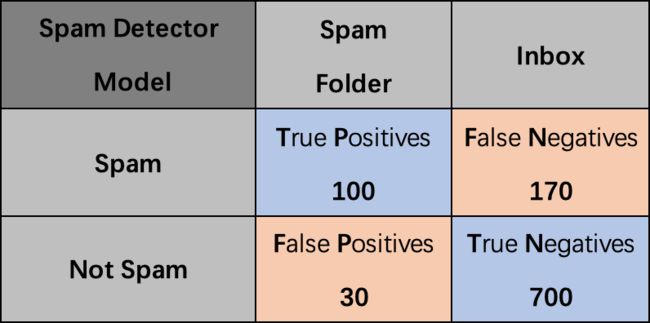
例2. 假设一个垃圾邮件过滤器模型，在270封垃圾邮件中，正确分类100封，错误分类170封；在730封正常邮件中，正确分类700封，错误分类30封，计算该分类器的准确率：

$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}=\frac{100+700}{100+30+700+170}=80\%$

1.3.1 准确率不适用的情形：信用卡欺诈检测模型（不平衡数据）

不平衡数据：一个类别比另一个类别出现次数多得多的数据集，对于不平衡数据，不适合使用准确流来评估模型。

我们来看一个准确率不适用的情形，假设我们建立一个检测信用卡欺诈行为的模型，数据中有284,335条良好交易记录、472条欺诈性交易数据，假设我们的模型预测结果如下：

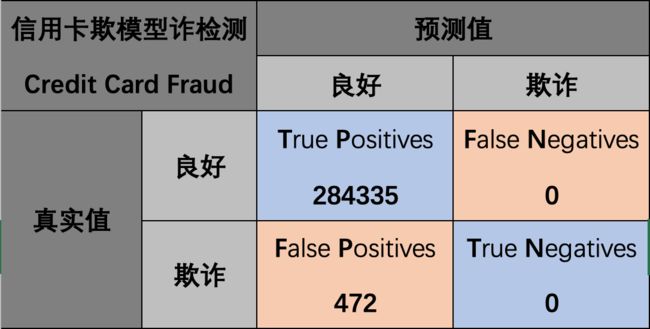
这个模型的准确率为：

$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}=\frac{284335+0}{284335+472+0+0}=99.83\%$

准确率很高，达到了$99.83\%$，但这并不说明这是一个好的模型，因为我们的模型是为了检测出欺诈数据，但这个模型一条欺诈数据也没有检测出来。因此在这个情形下，我们需要选择其他的评价指标来评价我们的模型。

1.4 精确率 Precision

精确率（Precision）：又称精度，体现分类器对整体的判断能力，即正确预测的比例（在所有预测为阳性的点中，真阳性的比例），计算公式如下：

$$Precision=\frac{TP}{TP+FP}\text{\hspace{1em}(5)}$$

1.4.1 精确率适用情形：垃圾邮件分类（高精度模型）

在垃圾邮件分类模型中，检测假阳性更重要：
假阴性意味着垃圾邮件将发到你的收件箱中。有点不太方便，但是可接受。而 假阳性意味着漏掉了重要的邮件，这是需要避免的。

例3. 以下面的图为例，
精确率为$\frac{100}{100+30}=76.9\%$，
召回率为$\frac{100}{100+170}=37.0$，
因此即使召回率只有$37.0\%$，但是精确率有$76.9\%$，所以我们仍称这是一个好的模型。

1.5 召回率 Recall

召回率（Recall）：又称灵敏度、真阳性率，为所有真实正样本中，分类器中能找到多少，计算公式如下：

$$Recall=\frac{TP}{TP+FN}\text{\hspace{1em}(6)}$$

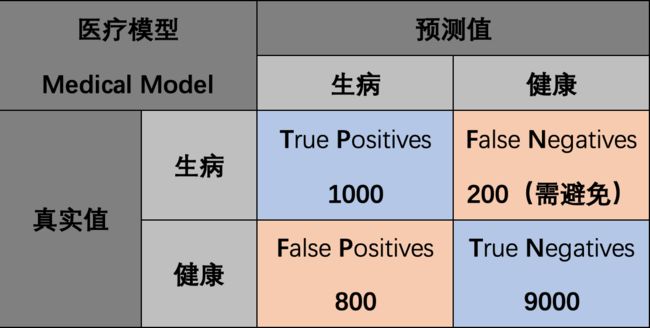
1.5.1 召回率适用情形：医疗模型

在医疗模型中，检测假阴性更重要：
假阳性意味着让健康人接受进一步检查，即使这意味会带来不便，但是可以接受。而假阴性以为着让病人错过治疗，这是更需要避免的。

例4. 以下面的图为例，精确率为$\frac{1000}{1000+800}=55.6\%$，召回率为$\frac{1000}{1000+200}=83.3$，因此即使精确率只有$55.6\%$，但是召回率有$83.3\%$，所以我们仍称这是一个好的模型。

1.6 F_1 Score

$F_1$ 得分是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的精确率和召回率。

$F_1$得分是精确率和召回率的一种调和平均，当精确率或召回率其中一个较小时，$F_1$ 得分将会较小；只有当两者都较大时，$F_1$ 得分才会接近1。

$$F_1=2\times \frac{Precision\times Recall}{Precision+Recall}\text{\hspace{1em}(7)}$$

$F_1$ 得分的取值域为$[0,1]$。

1.7 F_beta Score

$F_{\beta }$的物理意义就是将准确率和召回率这两个分值合并为一个分值，在合并的过程中，召回率的权重是准确率的$\beta$倍。$F_1$分数认为召回率和准确率同等重要，$F_2$分数认为召回率的重要程度是准确率的2倍，而$F_{0.5}$分数认为召回率的重要程度是准确率的一半。

$$F_{\beta }=(1+{\beta }^2)\frac{Precision\times Recall}{{\beta }^2\times Precision+Recall}\beta \in [0,+\infty )\text{\hspace{1em}(8)}$$

$F_{\beta }$ 得分的取值域为$[0,1]$。

• 当$\beta =1$时，即为 F1 得分：

  $F_{\beta =1}=(1+1)\frac{Precision\times Recall}{Precision+Recall}=2\times \frac{Precision\times Recall}{Precision+Recall}=F_1$

• 当$\beta =0$时，即为精确度：

  $F_{\beta =0}=(1+0)\frac{Precision\times Recall}{0\times Precision+Recall}=Precision$

• 当$\beta =\infty$时，即为召回率：

  $F_{\beta =N}=(1+N^2)\frac{Precision\times Recall}{N^2\times Precision+Recall}=\frac{Precision\times Recall}{\frac{N^2}{1+N^2}Precision+\frac{1}{1+N^2}Recall}$

  令$N\to \infty$，有：

  $\underset{N\to \infty }{\lim }{F}_N=\frac{Precision\times Recall}{1\times Precision+Recall}=Recall$

1.8 ROC 曲线

ROC 曲线：接受者操作特征曲线（Receiver Operating Characterostoc Curve ），roc曲线上每个点反映着对同一信号刺激的感受性。^[2]

x 轴：FPR 假阳性率（误诊率）$\frac{TP}{FP+TN}$

y 轴：TPR 真阳性率（召回率、灵敏度） $\frac{TP}{TP+FN}$

一般认为，如果 ROC 曲线是光滑的，那么基本可以判断没有太大的过拟合，AUC 面积越大一般认为模型更好。

ROC 曲线由来：ROC曲线，首先是由二战中的电子工程师和雷达工程师发明的，用来侦测战场上的敌军载具（飞机、船舰），也就是信号检测理论。之后很快就被引入了心理学来进行信号的知觉检测。此后被引入机器学习领域，用来评判分类、检测结果的好坏。因此，ROC曲线是非常重要和常见的统计分析方法。

以疾病检测为例，这是一个有监督的二分类模型，模型对每个样本的预测结果为一个概率值，我们需要从中选取一个阈值来判断健康与否。

定好一个阈值之后，超过此阈值定义为不健康，低于此阈值定义为健康，就可以得出混淆矩阵。

而如果在上述模型中我们没有定好阈值，而是将模型预测结果从高到低排序，将每次概率值依次作为阈值，那么就可以得到多个混淆矩阵。对于每个混淆矩阵，我们计算两个指标 TPR 和 FPR ,以 FPR 为 x 轴，TPR 为 y 轴画图，就得到了 ROC 曲线。

1.8.1 AUC

1. AUC：（Area under Curve）

AUC 被定义为ROC曲线下的面积，取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

2. AUC 的计算方法

非参数法：（两种方法实际证明是一致的）

(1) 梯形法则：早期由于测试样本有限，我们得到的AUC曲线呈阶梯状。曲线上的每个点向X轴做垂线，得到若干梯形，这些梯形面积之和也就是AUC 。

(2) Mann-Whitney统计量： 统计正负样本对中，有多少个组中的正样本的概率大于负样本的概率。这种估计随着样本规模的扩大而逐渐逼近真实值。

参数法：

(3) 主要适用于二项分布的数据，即正反样本分布符合正态分布，可以通过均值和方差来计算。

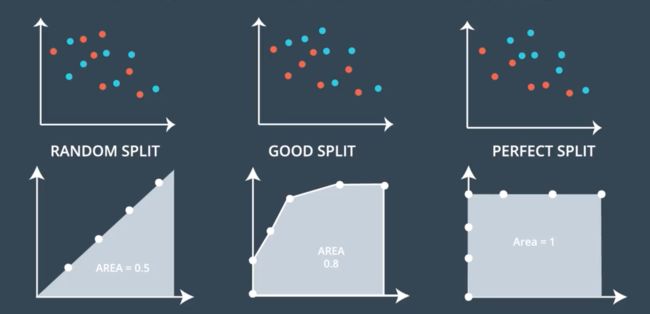
3. 从AUC判断分类器（预测模型）优劣的标准

(1) AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。

(2) 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

(3) AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。

(4) AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

三种 AUC 值的实例：

4. 不同模型 AUC 的比较

总的来说，AUC值越大，模型的分类效果越好，疾病检测越准确；不过两个模型AUC值相等并不代表模型效果相同，如下图中有三条ROC曲线，A模型比B和C都要好：

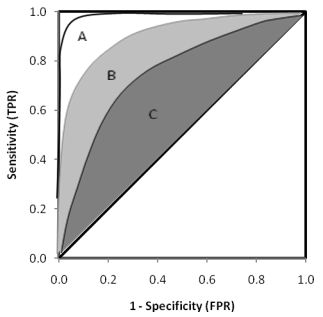
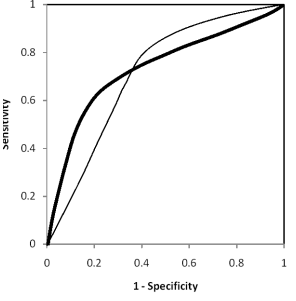
而下面两幅图中两条ROC曲线相交于一点，AUC值几乎一样：当需要高Sensitivity（TPR）时，模型A比B好；当需要高Speciticity（TNR）时，模型B比A好。

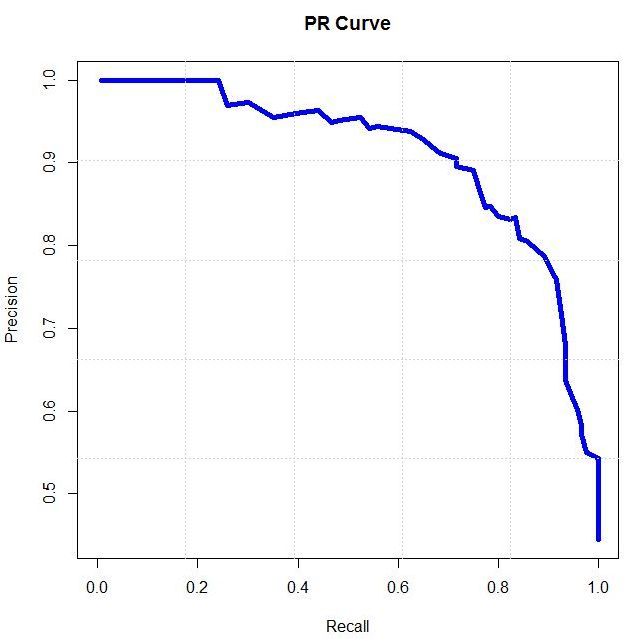
1.8.2 PR 曲线

1. PR 曲线：Precision Recall Curve，PR曲线和ROC曲线类似，ROC曲线是FPR和TPR的点连成的线，PR曲线是准确率和召回率的点连成的线。

x 轴：Recall（TPR，与 ROC 曲线的 y 轴相同）

y 轴：Precision 精确率

2. ROC曲线与PR曲线的取舍

相对来讲ROC曲线会稳定很多，在正负样本量都足够的情况下，ROC曲线足够反映模型的判断能力。因此，对于同一模型，PRC和ROC曲线都可以说明一定的问题，而且二者有一定的相关性，如果想评测模型效果，也可以把两条曲线都画出来综合评价。对于有监督的二分类问题，在正负样本都足够的情况下，可以直接用ROC曲线、AUC、KS评价模型效果。在确定阈值过程中，可以根据Precision、Recall或者F1来评价模型的分类效果。对于多分类问题，可以对每一类分别计算Precision、Recall和F1，综合作为模型评价指标。

在上图中，(a)和©为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果，©和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。

2. Sklearn 计算分类器性能指标

sklearn.metrics 官方文档

from sklearn.metrics import accuracy_score

y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
accuracy_score(y_true, y_pred)

0.5

• 分类报告，同时返回Precision、Recall、$F_1$ Score

  classification_report(y_true, y_pred[, …]) Build a text report showing the main classification metrics

• 混淆矩阵 Confusion Matrix

  metrics.confusion_matrix(y_true, y_pred[, …]) Compute confusion matrix to evaluate the accuracy of a classification

• 准确率 Accuracy

  metrics.accuracy_score(y_true, y_pred[, …]) Accuracy classification score.

• 平均准确率 average accuracy (TPR+TNR)/2

  metrics.balanced_accuracy_score(y_true, y_pred) Compute the balanced accuracy

• 精确率 Precision

  metrics.precision_score(y_true, y_pred[, …]) Compute the precision

• 召回率 Recall

  metrics.recall_score(y_true, y_pred[, …]) Compute the recall

• $F_1$ Score

  metrics.f1_score(y_true, y_pred[, labels, …]) Compute the F1 score, also known as balanced F-score or F-measure

• $F_{\beta }$ Score

  metrics.fbeta_score(y_true, y_pred, beta[, …]) Compute the F-beta score

• ROC 曲线

  metrics.roc_curve(y_true, y_score[, …]) Compute Receiver operating characteristic (ROC)

• AUC （梯型法）

  metrics.auc(x, y[, reorder]) Compute Area Under the Curve (AUC) using the trapezoidal rule

• AUC （Mann-Whitney统计量法）

  metrics.roc_auc_score(y_true, y_score[, …]) Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores.

• PR 曲线
  metrics.precision_recall_curve(y_true, …) Compute precision-recall pairs for different probability thresholds

参考资料

[1] klchang.混淆矩阵(Confusion matrix)的原理及使用(scikit-learn 和 tensorflow)[EB/OL].https://www.cnblogs.com/klchang/p/9608412.html, 2018-09-08.

[2] dzl_ML.分类器性能指标之ROC曲线、AUC值[EB/OL].https://www.cnblogs.com/dlml/p/4403482.html, 2015-04-08.