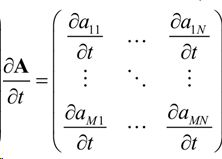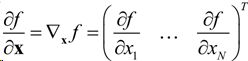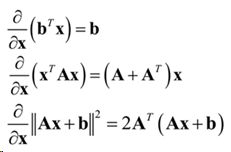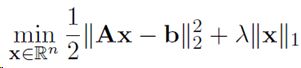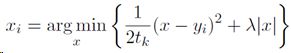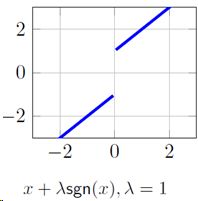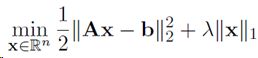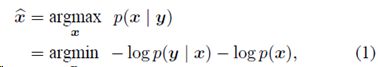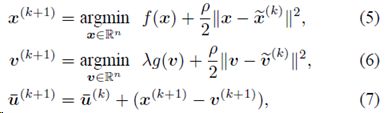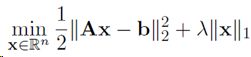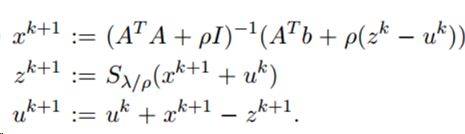主要关于ISTA和ADMM。
一些常用的矩阵和向量微分
矩阵A-标量t
标量函数f-矢量x
矢量函数g-矢量x
常用导数(b,x为向量,A为矩阵)
ISTA(Iterative Shrinkage-Thresholding Algorithm)
ISTA算法作用是求解以下形式目标函数
前一项为最小二乘数据拟合项,这一部分是可微的,可以用简单的梯度下降求解;后一项为L1范数惩罚项,作用是得到稀疏解。
ISTA的方法即将梯度下降的迭代解转换为
的形式,然后用软阈值方法求解。
梯度下降迭代解
考虑到如果没有惩罚项,梯度下降迭代解可以看作是使f的局部二次模型达到最小值时x的取值:
其中tk为步长。
加上惩罚项之后
令![]() ,转换为
,转换为
上式转换为
软阈值
如何求f(x)为最小值时x的取值?
f(x)中后一项|x|在0点不可微,但是凸函数,可以使用次梯度(subgradient)处理,|x|的次导数为sgn(x)
对f(x)求次梯度,并令次梯度为0:
考虑tk=1,λ=1的简单情况
![]()
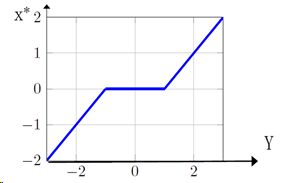
将y看作x*的函数:
旋转坐标轴:
软阈值函数即:
ISTA算法
综合以上两个部分,目标函数
可以通过以下式子更新迭代求解:
其中T是软阈值
ADMM最优化方法
主要思想是采用分裂的方法求解以下方程:
Chan S H , Wang X , Elgendy O A . Plug-and-Play ADMM for Image Restoration: Fixed Point Convergence and Applications[J]. IEEE Transactions on Computational Imaging, 2016, 3(1):84-98.
这篇文章介绍了ADMM(交替方向乘子)方法,这是一种在图像恢复中广泛应用的约束优化方法,主要优点在于具有模块化的结果,可以作为子算法模块插入现成的图像降噪算法中,但收敛条件和速度还要看具体算法的实现情况。
MAP
最大后验概率(MAP):
(1)与下式等价:
![]()
其中![]()
这是个无约束优化问题(unconstrained optimization),可以用ADMM求解。
ADMM
ADMM的主要思想是通过分裂变量将无约束优化问题转化为约束问题,然后交替迭代求解。
将变量x分裂为x和v,x=v,上式转化为:
其增广拉格朗日函数为:
其中,增设一个变量u,称为拉格朗日算子(又称对偶变量),添加了惩罚函数(ρ 项)。
根据ADMM,根据以下步骤重复迭代,交替对x,v,u进行更新:
收敛到增广拉格朗日函数的鞍点。
在交替迭代的步骤中,(5)可以看作一个反演过程,涉及前向成像模型f(x),(6)可以看做降噪噪过程,涉及到先验g(v)。
令σ = √ λ/ρ,(6)变为:
将v(k)项视为含噪声图像,(8)最小化无噪声图像v和v(k)之间的残差,如果先验g(v)为全变差范数(total variation norm),(8)为标准全变差去噪问题。
ADMM举例-lasso
http://web.stanford.edu/~boyd/papers/admm/
目标函数
写成 ADMM 形式
更新步骤:
Matlab代码:
测试:
randn('seed', 0);
rand('seed',0);
m = 1500; % number of examples
n = 5000; % number of features
p = 100/n; % sparsity density
x0 = sprandn(n,1,p);
A = randn(m,n);
A = A*spdiags(1./sqrt(sum(A.^2))',0,n,n); % normalize columns
b = A*x0 + sqrt(0.001)*randn(m,1);
lambda_max = norm( A'*b, 'inf' );
lambda = 0.1*lambda_max;
程序代码: function [z, history] = lasso_via_ADMM(A, b, lambda, rho, alpha) % Solve lasso problem via ADMM % objective function: % minimize 1/2*|| Ax - b ||_2^2 + \lambda || x ||_1 % The solution is returned in the vector x. % rho is the augmented Lagrangian parameter. % alpha is the over-relaxation parameter (typical values for alpha are % between 1.0 and 1.8). %%% Global constants and defaults %%%% MAX_ITER = 1000; ABSTOL = 1e-4; RELTOL = 1e-2; %%%% Data preprocessing %%%% [m, n] = size(A); Atb = A'*b; %%%% ADMM solver %%%% x = zeros(n,1); z = zeros(n,1); u = zeros(n,1); for k = 1:MAX_ITER % x-update [m,n] = size(A); temp = Atb + rho*(z - u); if(m<n) L = chol( speye(m) + 1/rho*(A*A'), 'lower' ) L = sparse(L); U = sparse(L'); x = temp/rho - (A'*(U \ ( L \ (A*temp) )))/rho^2; else L = chol( A'*A + rho*speye(n), 'lower' ); L = sparse(L); U = sparse(L'); x = U \ (L \ q); end % z-update with relaxation zold = z; x_hat = alpha*x + (1 - alpha)*zold; z = soft_threshold(x_hat + u, lambda/rho); % u-update u = u + (x_hat - z); % diagnostics, reporting, termination checks r_norm = norm(x - z); s_norm = norm(-rho*(z - zold)); eps_pri = sqrt(n)*ABSTOL + RELTOL*max(norm(x), norm(-z)); eps_dual = sqrt(n)*ABSTOL + RELTOL*norm(rho*u); if (r_norm < eps_pri && s_norm < eps_dual) break; end end end %soft_threshold function z = soft_threshold(x,kappa) z = sign(x).*max(abs(x)-kappa,0); end