bfs广度优先搜索算法_C语言中的广度优先搜索（BFS）程序

bfs广度优先搜索算法

In this tutorial we will discuss about Breadth First Search or BFS program in C with algorithm and an example. Before jumping to actual coding lets discuss something about Graph and BFS.

在本教程中，我们将讨论带有算法的C语言中的“广度优先搜索”或BFS程序。 在进行实际编码之前，让我们讨论一下有关Graph和BFS的知识。

Also Read: Depth First Search (DFS) Traversal of a Graph [Algorithm and Program]

另请参阅：图的深度优先搜索(DFS)遍历[算法和程序]

A Graph G = (V, E) is a collection of sets V and E where V is a collection of vertices and E is a collection of edges.

图G =(V，E)是集合V和E的集合，其中V是顶点的集合，E是边的集合。

A Graph can be of two types: 1. Directed Graph 2. Undirected Graph

图可以有两种类型： 1 .有向图2.无向图

In data structures, there is a popular term known as ‘Traversal’. It is the process of systematically visiting or examining (may be to update the Graph nodes) each node in a tree data structure, exactly once.

在数据结构中，有一个流行的术语称为“ Traversal”。 这是系统访问或检查树数据结构中的每个节点(一次)的过程(可能是更新Graph节点)。

There are two most common methods to traverse a Graph: 1. Breadth First Search 2. Depth First Search

遍历图有两种最常见的方法： 1.广度优先搜索 2.深度优先搜索

In this tutorial, we are going to focus on Breadth First Search technique.

在本教程中，我们将专注于广度优先搜索技术。

In this technique, we first visit the vertex and then visit all the vertices adjacent to the starting vertex i.e., 0. Next, we pick the adjacent vertices one after another and visit their adjacent vertices and this process goes on and on until we reach the last vertex.

在此技术中，我们首先访问顶点，然后访问与起始顶点相邻的所有顶点，即0。接下来，我们一个接一个地选择相邻的顶点，然后访问它们的相邻顶点，此过程不断进行，直到到达顶点为止。最后一个顶点。

广度优先搜索(BFS)示例 (Breadth First Search (BFS) Example)

Consider below Graph as an example.

以下面的图表为例。

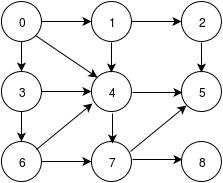
The vertex 0 is the starting vertex in our case. We start our traversal from the vertex 0. Then we will visit all vertices adjacent to vertex 0 i.e., 1, 4, 3. Here, we can visit these three vertices in any order. Suppose we visit the vertices in order 1,3,4.

在我们的例子中，顶点0是起始顶点。 我们从顶点0开始遍历。然后，我们将访问与顶点0相邻的所有顶点，即1、4、3。在这里，我们可以按任何顺序访问这三个顶点。 假设我们按1,3,4的顺序访问顶点。

The traversal would be: 0 1 3 4

遍历为：0 1 3 4

Now, we shall visit all the vertices adjacent to 1, then all the vertices adjacent to 3 and then all the vertices adjacent to 4. So first we shall visit 2 (since it is adjacent to 1), then 6 (since it is adjacent to 3) and 5, 7 (since these are adjacent to 4).

现在，我们将访问与1相邻的所有顶点，然后访问与3相邻的所有顶点，然后访问与4相邻的所有顶点。因此，首先，我们将访问2(因为它与1相邻)，然后是6(由于它相邻)。至3)和5、7(因为它们与4相邻)。

Note: Vertex 4 is adjacent to vertices 1 and 3, but it has already been visited so we’ve ignored it.

注意：顶点4与顶点1和3相邻，但是已经被访问过，因此我们忽略了它。

The traversal would be: 0 1 3 4 2 6 5 7

遍历为：0 1 3 4 2 6 5 7

Now, we shall visit all the vertices adjacent to 2, 6, 5, and 7 one by one. We can see that vertex 5 is adjacent to vertex 2. Since, it has already been traversed upon before, we have don’t need to traverse through it again and move on to the next vertex. Now, the vertices 4 and 7 are adjacent to the vertex 6. Since, they have been traversed upon before, we will not traverse on them again. Vertex 5 does not have any adjacent vertices. Vertices 5 and 8 are adjacent to vertex 7. Since, vertex 5 has been traversed upon before, we will not traverse it again. However, vertex 8 has not yet been visited. So we will traverse on vertex 8.

现在，我们将逐一访问与2、6、5和7相邻的所有顶点。 我们可以看到顶点5与顶点2相邻。由于之前已经遍历了顶点5，因此无需再次遍历它就可以移动到下一个顶点。 现在，顶点4和7与顶点6相邻。由于之前已遍历它们，因此我们不再在其上遍历。 顶点5没有任何相邻的顶点。 顶点5和8与顶点7相邻。由于之前已经遍历了顶点5，所以我们不再对其进行遍历。 但是，尚未访问顶点8。 因此，我们将在顶点8上遍历。

The traversal would be: 0 1 3 4 2 6 5 7 8

遍历为：0 1 3 4 2 6 5 7 8

Now, we need to visit vertices adjacent to vertex 8. However, there is no vertex adjacent to vertex 8 and hence we will have to stop the traversal here.

现在，我们需要访问顶点8附近的顶点。但是，顶点8附近没有顶点，因此我们必须在此处停止遍历。

Note: There’s no unique traversal and it can be different based on the order of the successors.

注意：没有唯一的遍历，并且根据后继的顺序可以不同。

We shall look at a BFS program in C for directed Graph using a Queue. This program reaches only those vertices that are reachable from the start vertex.

我们将使用Queue在C中的BFS程序中查找有向图。 该程序仅到达从起始顶点可到达的那些顶点。

C语言中的广度优先搜索(BFS)程序 (Breadth First Search (BFS) Program in C)

#include
#include
 
#define MAX 100  
 
#define initial 1
#define waiting 2
#define visited 3
 
int n;    
int adj[MAX][MAX];
int state[MAX]; 
void create_graph();
void BF_Traversal();
void BFS(int v);
 
int queue[MAX], front = -1,rear = -1;
void insert_queue(int vertex);
int delete_queue();
int isEmpty_queue();
 
int main()
{
	create_graph();
	BF_Traversal();
	return 0;
}
 
void BF_Traversal()
{
	int v;
	
	for(v=0; v rear)
		return 1;
	else
		return 0;
}
 
int delete_queue()
{
	int delete_item;
	if(front == -1 || front > rear)
	{
		printf("Queue Underflow\n");
		exit(1);
	}
	
	delete_item = queue[front];
	front = front+1;
	return delete_item;
}
 
void create_graph()
{
	int count,max_edge,origin,destin;
 
	printf("Enter number of vertices : ");
	scanf("%d",&n);
	max_edge = n*(n-1);
 
	for(count=1; count<=max_edge; count++)
	{
		printf("Enter edge %d( -1 -1 to quit ) : ",count);
		scanf("%d %d",&origin,&destin);
 
		if((origin == -1) && (destin == -1))
			break;
 
		if(origin>=n || destin>=n || origin<0 || destin<0)
		{
			printf("Invalid edge!\n");
			count--;
		}
		else
		{
			adj[origin][destin] = 1;
		}
	}
}

Output

输出量

If you find anything incorrect or have any doubts regarding above Breadth First Search (BFS) program in C then comment below.

如果您发现任何错误或对C语言中的“广度优先搜索(BFS)”程序有任何疑问，请在下面评论。

翻译自: https://www.thecrazyprogrammer.com/2015/09/breadth-first-search-bfs-program-in-c.html

bfs广度优先搜索算法