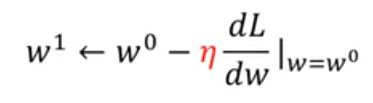机器学习-regression回归

本文只是本人理解，若有偏差与错误欢迎指正

回归：回归就是首先提出实验模型，但是模型的关键参数未知，通过大量数据来求出最符合测试数据的实验模型，也就是求出模型的关键参数；接下来利用李宏毅授课中的一个例子来具体看看什么是regression

这是一个很有趣的例子，评估口袋妖怪进化之后的战斗能力（CP）

其中包含其他的一些属性，Xcp，Xs,Xhp,Xw,Xh等

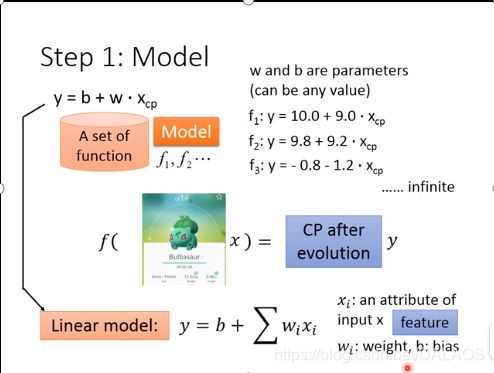
第一步是确定一个Model（模型），这里确定了一个线性模型，也可以这样表示b,w是参数可以为任意数据，Xi是口袋妖怪的各种属性，w可以理解为权重，b可以理解为偏差。

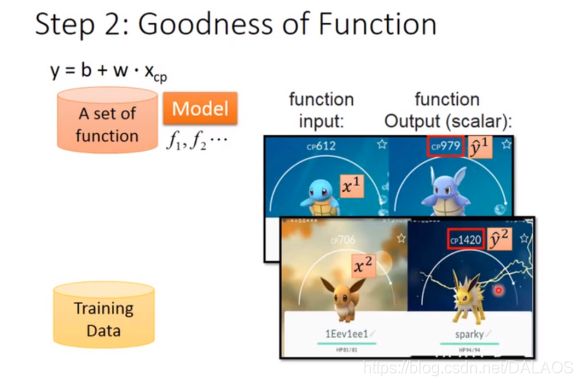
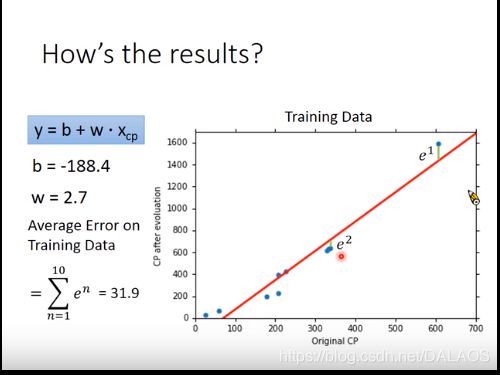
第二步确定这些函数那些是好的，其实也就是确定b,w，首先收集口袋妖怪的进化数据，

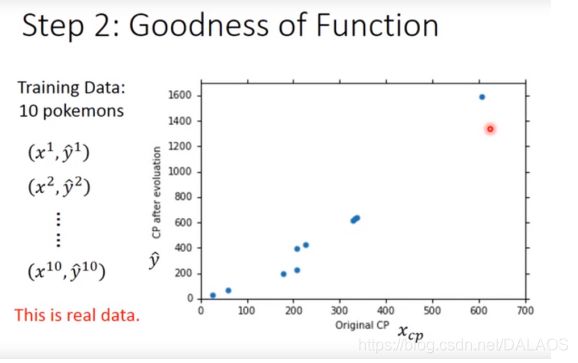
下边是收集的10个数据（感觉好少），以及他们的进化之前与进化之后的数据二维图，是不是到这里感觉像概率论上学的东西，其实就是要找到一条直线使这些点尽可能的靠近，就用到了最小二乘法；

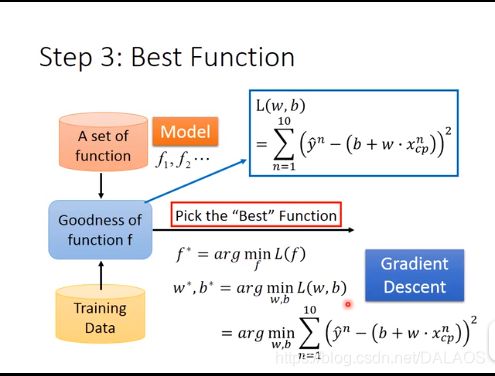
用最小二乘法来求解b,w;用到了loss function L,其实它就是均方误差，越小越好；求解b,w是的L

最小化的过程称为线性回归模型的最小二乘法参数估计；

图中每一个点代表一个模型函数，颜色代表均方误差，蓝色代表好，红色代表差

第三步就是选出最好的function，也就是L的最小值，这就用到了微分求导，这里用到的方法是梯度下降法

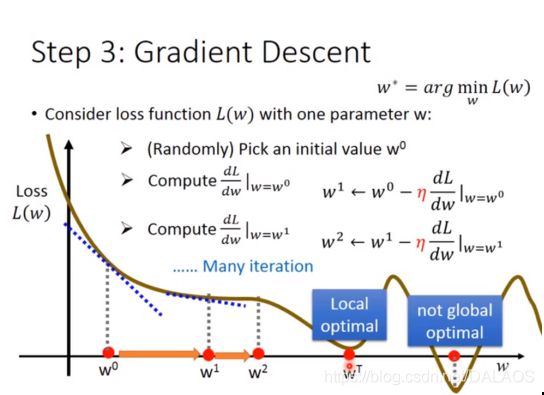
梯度下降：这里我们先按一维算只有一个未知数w

1、随机选取一个初始点

2、计算导数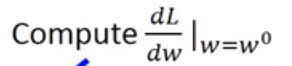如果是负数增加w的值，如果是正数就减少w，其实这就确定了下降的方向，这个叫学习率，wi增加或者减少的多少取决于这个导数和学习率，

这样求得第二个点

3、重复第二步一直找到local optical，

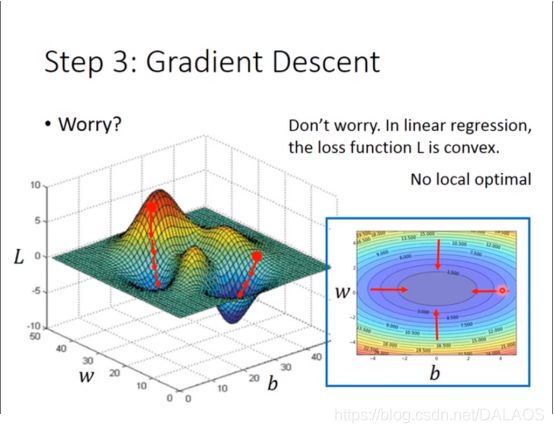
其实大家很疑惑这样只能找到局部最优，其实在这种模型下不存在局部最优的

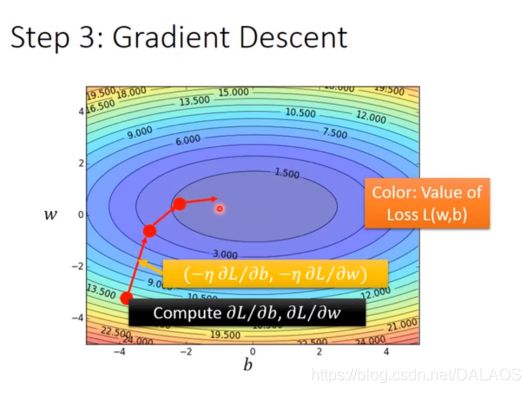
在两个参数下：用到了偏导数，其他和一个参数的基本一样，你们自己看去吧（哈哈），还有一点两个参数下也不存在局部最优；

这个是解题步骤的图解

 

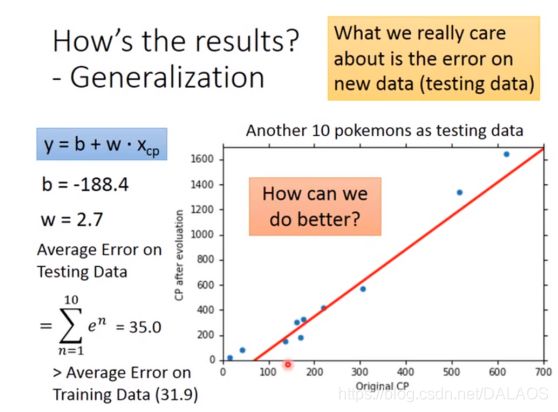
这样这个模型我就求出来了：计算平均错误率，这个就是样本到直线的竖直距离之和；我们更关心测试的平均错误率，测试的平均错误率还稍微大于平均错误率，那我们应该怎样做的更好一些呢：

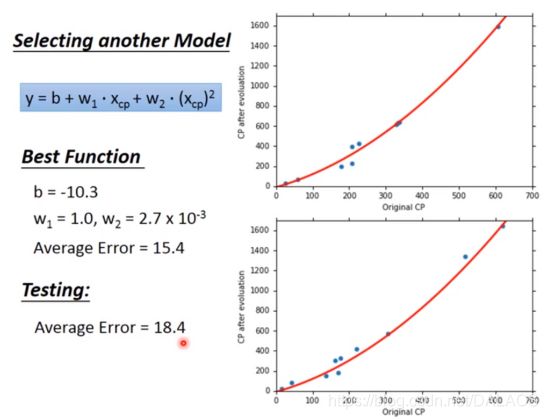
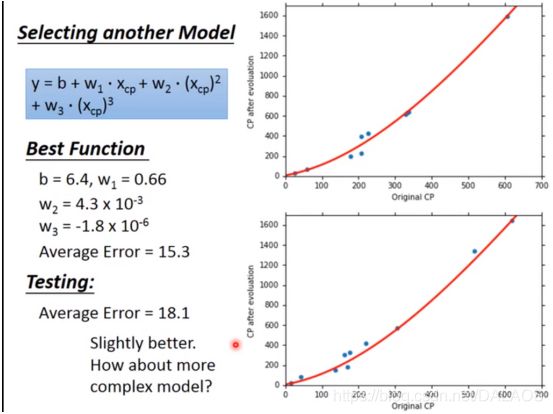
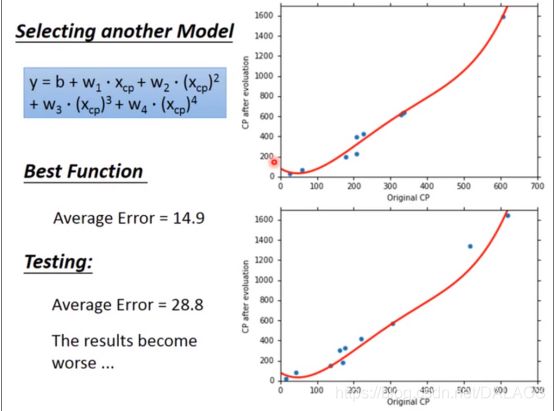
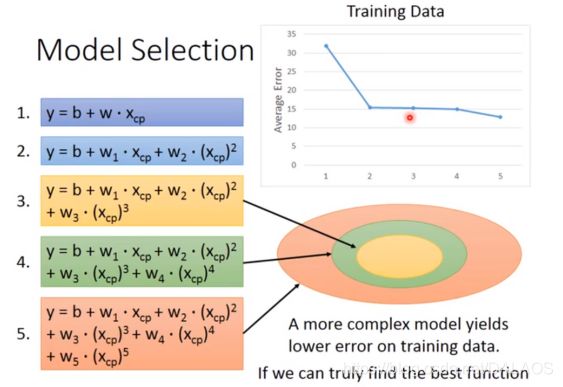
第一种：采用二次方的形式，效果明显比一次的好，还要做的更好我们就使用了三次方、四次方、五次方：

不难发现，训练结果越来越好，但是四次五次测试结果变坏了，并且五次方时出现了不合理的结果，出现了负数，其实这就是过度拟合

 

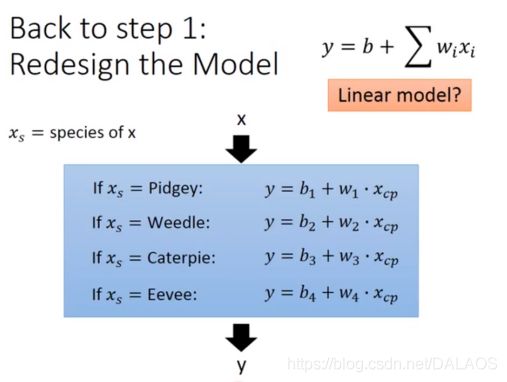
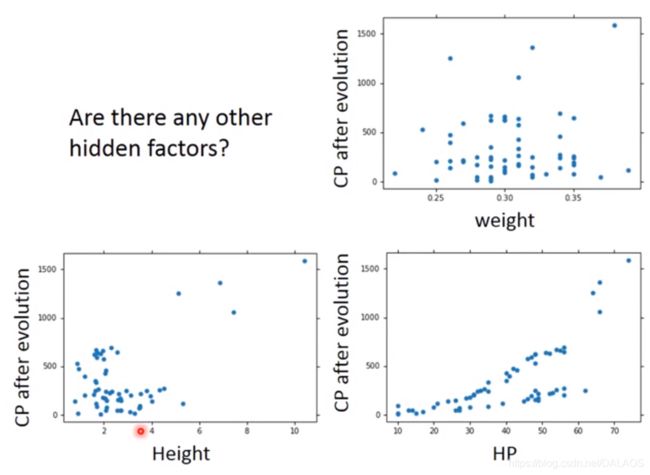
上边我们说到我们收集的数据太少，现在我们收集大量数据：不难发现好像我们上边的工作白忙活了，就不是简单的线性关系了，我们还可以发现，他们的分布还与他们的种类有关系，也就是说我们只看他的一个属性（cp）是不够的：

我们有另一种处理方式，采用如下线性结构：

根据0、1有如下等式，有助于理解

求得如下模型不难发现效果比上边的好，但是还是有在直线上下的点我们要考虑其他的属性：

我们可以把所有想到的属性全部填进去，但是发现训练效果好，测试效果很差，我们采用另一种方式调整：

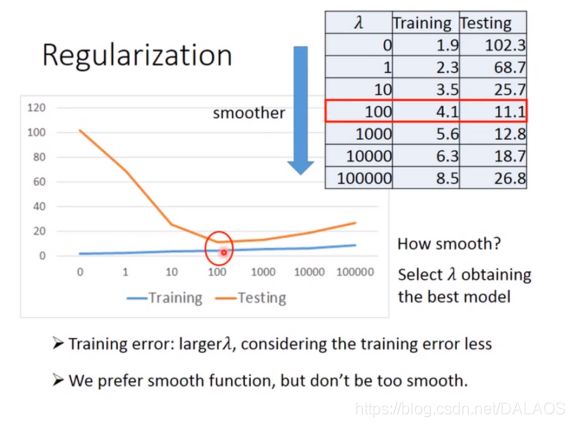
wi越小越好，这样使得结果更加平滑，是一个确定的数，

这是实验的结果：大家看看能看懂不，我就懒得写了

##############我来给大家演示一下代码###########################

这是之后又添加上去的代码

##李弘毅线性回归模型demo
#y_data = b + w*x_data

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import  numpy as np

x_data = [338.,333.,328.,207.,226.,25.,179.,60.,208.,606.]
y_data = [640.,633.,619.,393.,428.,27.,193.,66.,226.,1591.]

b = -120
w = -4
lr = 1##学习率//这个是添加lr_b，lr_w之后随意设置的

iteration = 100000###迭代次数
##求值过程之中b，w的保存用于画图
b_history = [b]
w_history = [w]
############添加lr_b，lr_w效果更好一些，这涉及到一个方法以后会写
lr_b = 0.0
lr_w = 0.0
############
for i in range(iteration):
    ##偏导
    b_grad = 0.0;
    w_grad = 0.0;

    for n in range(len(x_data)):
        b_grad = b_grad-2.0*(y_data[n]-b-w*x_data[n])*1.0
        w_grad = w_grad-2.0*(y_data[n]-b-w*x_data[n])*x_data[n]
#################################
    lr_b = lr_b + b_grad ** 2
    lr_w = lr_w + w_grad ** 2
################################
##更新b，w的值  b0->b1 w0->w1
    b = b - lr/(np.sqrt(lr_b))*b_grad
    w = w - lr/(np.sqrt(lr_w))*w_grad
##将数据保存，用于画图
    b_history.append(b)
    w_history.append(w)
    
#################作图准备工作########################
x = np.arange(-200,-100,1)##bias
y = np.arange(-5,5,0.1)##weight
Z =np.zeros((len(x),len(y)))
X,Y = np.meshgrid(x,y)
for i in range(len(x)):
    for j in range(len(y)):
        b= x[i]
        w = y[j]
        Z[j][i] = 0
        for n in range(len(x_data)):
            Z[j][i]  = Z[j][i] + (y_data[n] -b -w*x_data[n])**2
        Z[j][i] = Z[j][i]/len(x_data)
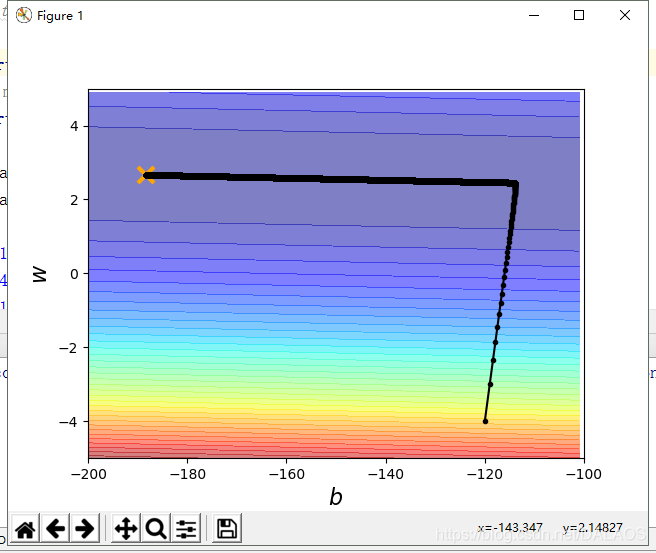
###########################作图###########################
plt.contourf(x,y,Z,50,alpha=0.5,cmap=plt.get_cmap('jet'))
plt.plot([-188.4],[2.67],'x',ms=12,markeredgewidth=3,color='orange')
plt.plot(b_history,w_history,'o-',ms=3,lw=1.5,color='black')
plt.xlim(-200,-100)
plt.ylim(-5,5)
plt.xlabel(r'$b$',fontsize=16)
plt.ylabel(r'$w$',fontsize=16)
plt.show()

效果图：