Codeforces Round #703 (Div. 2) 题解
比赛链接
A - Shifting Stacks
最优情况是![]() 。
。
#include
using namespace std ;
int main()
{
std::ios::sync_with_stdio(false) , cin.tie(0) ;
int T ;
cin >> T ;
while(T --)
{
int n ;
cin >> n ;
vector a(n) ;
for(int i = 0 ; i < n ; i ++) cin >> a[i] ;
bool flag = true ;
for(int i = 0 ; i < n ; i ++)
{
if(a[i] < i)
{
flag = false ;
break ;
}
else
{
long long t = a[i] - i ;
a[i] -= t ;
if(i + 1 < n) a[i + 1] += t ;
}
}
if(flag) cout << "YES\n" ;
else cout << "NO\n" ;
}
return 0 ;
}
B - Eastern Exhibition
一个经典结论就是![]() 最小化的
最小化的![]() 是
是![]() 的中位数,如果
的中位数,如果![]() 是偶数,那么
是偶数,那么![]() 是中间的一段区间。
是中间的一段区间。
![]() 轴分别算再相乘即可。
轴分别算再相乘即可。
#include
using namespace std ;
int main()
{
std::ios::sync_with_stdio(false) , cin.tie(0) ;
int T ;
cin >> T ;
while(T --)
{
int n ;
cin >> n ;
vector x(n) , y(n) ;
for(int i = 0 ; i < n ; i ++) cin >> x[i] >> y[i] ;
sort(x.begin() , x.end()) ;
sort(y.begin() , y.end()) ;
int cnt1 = x[n / 2] - x[(n - 1) / 2] + 1 ;
int cnt2 = y[n / 2] - y[(n - 1) / 2] + 1 ;
cout << 1ll * cnt1 * cnt2 << '\n' ;
}
return 0 ;
}
C2 - Guessing the Greatest (hard version)
第一次询问: id=ask(1,n)。
第二次询问:m=ask(1,id-1)。可以知道最大值在[1,id-1]还是[id+1.n]。
剩下log次询问:假如最大值在id左侧,通过ask(m,id)=id找到最大的m就是答案。
#include
using namespace std ;
int ask(int l , int r)
{
printf("? %d %d\n" , l , r) ;
fflush(stdout) ;
int y ;
scanf("%d" ,&y) ;
return y ;
}
int main()
{
int n ;
scanf("%d" , &n) ;
int id = ask(1 , n) ;
int m ;
if(id == 1) m = n ;
else if(id == n) m = 1 ;
else
{
if(ask(1 , id) == id) m = 1 ;
else m = n ;
}
if(m < id)
{
int ll = 1 , rr = id - 1 ;
while(ll <= rr)
{
int mid = (ll + rr) / 2 ;
if(ask(mid , id) == id) m = mid , ll = mid + 1 ;
else rr = mid - 1 ;
}
}
else
{
int ll = id + 1 , rr = n ;
while(ll <= rr)
{
int mid = (ll + rr) / 2 ;
if(ask(id , mid) == id) m = mid , rr = mid - 1 ;
else ll = mid + 1 ;
}
}
printf("! %d\n" , m) ;
fflush(stdout) ;
return 0 ;
}
D - Max Median
二分答案就好啦。check(x)的时候对于大于等于x的数就标记为1,其他数标记为-1。一段长度不小于k的连续子序列的和大于0,那么就合法。
#include
using namespace std ;
const int maxn = 2e5 + 10 ;
int a[maxn] ;
int mn[maxn << 2] ;
int n , k ;
int ls(int x)
{
return x << 1 ;
}
int rs(int x)
{
return x << 1 | 1 ;
}
void update(int id , int l , int r , int x , int y)
{
int mid = (l + r) / 2 ;
if(l == r && l == x){mn[id] = y ; return ;}
if(x <= mid) update(ls(id) , l , mid , x , y) ;
else update(rs(id) , mid + 1 , r , x , y) ;
mn[id] = min(mn[ls(id)] , mn[rs(id)]) ;
}
int query(int id , int l , int r , int x , int y)
{
int ans = 1e9 ;
int mid = (l + r) / 2 ;
if(y < x) return 0 ;
if(x <= l && r <= y) return mn[id] ;
if(x <= mid) ans = min(ans , query(ls(id) , l , mid , x , y)) ;
if(y > mid) ans = min(ans , query(rs(id) , mid + 1 , r , x , y)) ;
return ans ;
}
bool ok(int x)
{
int now = 0 ;
memset(mn , 0x3f , sizeof(mn)) ;
for(int i = 1 ; i <= n ; i ++)
{
if(a[i] >= x) now ++ ;
else now -- ;
update(1 , 1 , n , i , now) ;
if(i >= k)
{
int t = query(1 , 1 , n , i , i) ;
if(t > 0)
{
return true ;
}
if(i > k)
{
if(query(1 , 1 , n , 1 , i - k) < t) return true ;
}
}
}
return false ;
}
int main()
{
std::ios::sync_with_stdio(false) , cin.tie(0) ;
cin >> n >> k ;
for(int i = 1 ; i <= n ; i ++) cin >> a[i] ;
int ans = 1 ;
int l = 1 , r = n ;
while(l <= r)
{
int mid = (l + r) / 2 ;
if(ok(mid)) ans = mid , l = mid + 1 ;
else r = mid - 1 ;
}
cout << ans << '\n' ;
return 0 ;
}
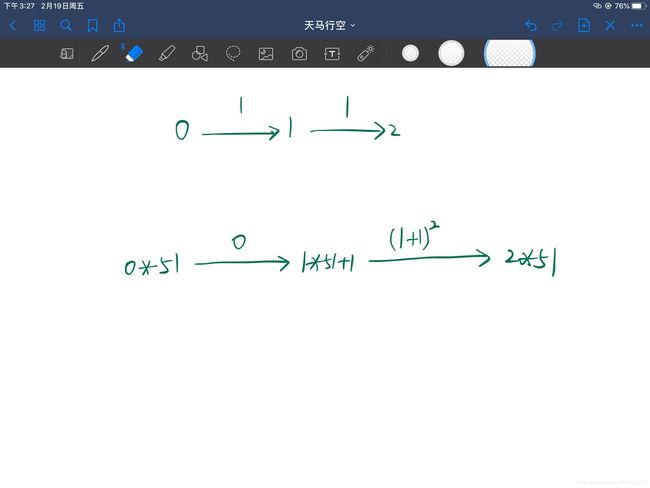
E - Paired Payment
主要是建立一些虚点和虚边,然后跑一下dij。参考上图和代码。
#include
#define pb push_back
#define fi first
#define se second
#define sz(x) (int)x.size()
#define cl(x) x.clear()
#define all(x) x.begin() , x.end()
#define rep(i , x , n) for(int i = x ; i <= n ; i ++)
#define per(i , n , x) for(int i = n ; i >= x ; i --)
#define mem0(x) memset(x , 0 , sizeof(x))
#define mem_1(x) memset(x , -1 , sizeof(x))
#define mem_inf(x) memset(x , 0x3f , sizeof(x))
#define debug(x) cerr << #x << " = " << x << '\n'
#define ddebug(x , y) cerr << #x << " = " << x << " " << #y << " = " << y << '\n'
#define ios std::ios::sync_with_stdio(false) , cin.tie(0)
using namespace std ;
typedef long long ll ;
typedef long double ld ;
typedef pair pii ;
typedef pair pll ;
typedef double db ;
const int mod = 998244353 ;
const int maxn = 1e7 + 1e6 + 10 ;
const int inf = 0x3f3f3f3f ;
const double eps = 1e-6 ;
typedef pair pli ; //��Ȩlong long
struct Link
{
int num , head[maxn] ;
struct Edge
{
int v , next ;
int w ;
} edge[maxn << 1] ;
void init()
{
num = 0 ;
memset(head , -1 , sizeof(head)) ;
}
void add(int u , int v , int w)
{
edge[num].v = v ;
edge[num].w = w ;
edge[num].next = head[u] ;
head[u] = num ++ ;
}
} link ;
struct Dij
{
int dis[maxn] ;
priority_queue , greater > q ;
void init()
{
memset(dis , 0x3f , sizeof(dis)) ;
}
void dijkstra(int s)
{
dis[s] = 0 ;
q.push(make_pair(0 , s)) ;
while(!q.empty())
{
pii p = q.top() ;
q.pop() ;
int u = p.second ;
if(p.first != dis[u]) continue ; //�Ż������þ�ֵ���¡�
for(int i = link.head[u] ; i != -1 ; i = link.edge[i].next)
{
int v = link.edge[i].v ;
int w = link.edge[i].w ;
if(dis[v] > dis[u] + w)
{
dis[v] = dis[u] + w ;
q.push(make_pair(dis[v] , v)) ;
}
}
}
}
} dij ;
int main()
{
ios ;
link.init() ;
dij.init() ;
int n , m ;
cin >> n >> m ;
while(m --)
{
int u , v , w ;
cin >> u >> v >> w ;
u -- , v -- ;
link.add(u * 51 , v * 51 + w , 0) ;
for(int i = 1 ; i <= 50 ; i ++)
link.add(u * 51 + i , v * 51 , (i + w) * (i + w)) ;
swap(u , v) ;
link.add(u * 51 , v * 51 + w , 0) ;
for(int i = 1 ; i <= 50 ; i ++)
link.add(u * 51 + i , v * 51 , (i + w) * (i + w)) ;
}
dij.dijkstra(0) ;
for(int i = 0 ; i < n ; i ++) if(dij.dis[i * 51] > 1e9) dij.dis[i * 51] = -1 ;
for(int i = 0 ; i < n ; i ++) cout << dij.dis[i * 51] << " \n"[i == n - 1] ;
return 0 ;
}
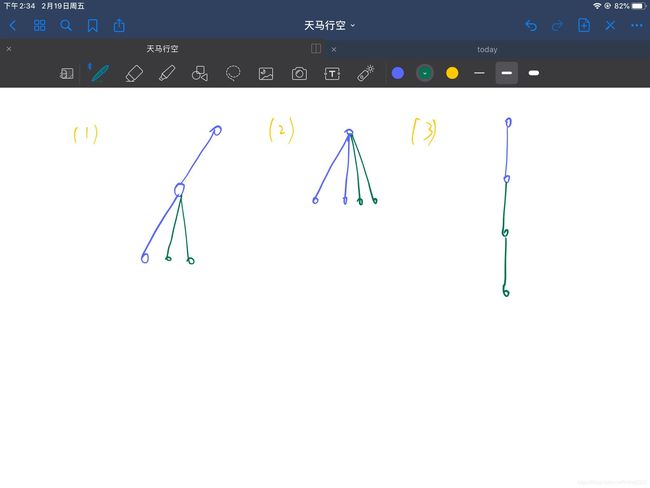
F - Pairs of Paths
总共就这三种情况。分类讨论即可。耐心写。
时间复杂度:![]() 。常数有点大。
。常数有点大。![]() 可以去掉,但是时限很宽裕,不去掉好写一些。
可以去掉,但是时限很宽裕,不去掉好写一些。
#include
using namespace std ;
const int maxn = 3e5 + 10 ;
int n , m ;
vector g[maxn] ;
int dep[maxn] , fa[maxn][25] ;
int now ;
int dfn[maxn] , sz[maxn] ;
vector> s[maxn] ;
int c[maxn] ; // c[u]表示一个端点在u子树内部,另一个端点在u子树外部
map d[maxn] ;
void dfs1(int f , int u , int deep)
{
dfn[u] = ++ now ;
sz[u] = 1 ;
dep[u] = deep ;
for(int i = 1 ; i <= 20 ; i ++)
{
int nxt = fa[u][i - 1] ;
fa[u][i] = fa[nxt][i - 1] ;
}
for(auto v : g[u])
{
if(v == f) continue ;
fa[v][0] = u ;
dfs1(u , v , deep + 1) ;
sz[u] += sz[v] ;
s[u].push_back({dfn[v] , v}) ;
}
}
int lca(int x , int y)
{
if(dep[x] < dep[y]) swap(x , y) ;
for(int i = 20 ; i >= 0 ; i --)
if(dep[fa[x][i]] >= dep[y])
x = fa[x][i] ;
if(x == y) return x ;
for(int i = 20 ; i >= 0 ; i --)
if(fa[x][i] != fa[y][i])
x = fa[x][i] , y = fa[y][i] ;
return fa[x][0] ;
}
vector> p[maxn] ;
int cnt[maxn] ;
int change(int lc , int u)
{
pair tt = {dfn[u] , 1000000000} ;
auto it = upper_bound(s[lc].begin() , s[lc].end() , tt) ;
it -- ;
d[lc][(*it).second] ++ ;
return (*it).second ;
}
long long cal1() //same lca
{
long long res = 0 ;
for(int i = 1 ; i <= n ; i ++)
{
int siz = p[i].size() ;
sort(p[i].begin() , p[i].end()) ;
res += 1ll * siz * (siz - 1) ;
for(int j = 0 ; j < siz ; j ++)
{
if(p[i][j].first != -1) cnt[p[i][j].first] ++ ;
if(p[i][j].second != -1) cnt[p[i][j].second] ++ ;
}
for(int j = 0 ; j < siz ; j ++)
{
int k = j ;
while(k + 1 < siz && p[i][k + 1] == p[i][k]) k ++ ;
for(int t = j ; t <= k ; t ++)
{
if(p[i][t].first == -1 && p[i][t].second == -1) continue ;
else if(p[i][t].second == -1)
{
int num = cnt[p[i][t].first] - 1 ;
res -= num ;
}
else
{
int num = cnt[p[i][t].first] - 1 ;
num += cnt[p[i][t].second] - 1 ;
num -= (k - j + 1) - 1 ;
res -= num ;
}
}
j = k ;
}
for(int j = 0 ; j < siz ; j ++)
{
if(p[i][j].first != -1) cnt[p[i][j].first] = 0 ;
if(p[i][j].second != -1) cnt[p[i][j].second] = 0 ;
}
}
return res / 2 ;
}
long long cal2(int fa , int u) //not same lca
{
long long res = 0 ;
for(auto v : g[u])
{
if(v == fa) continue ;
res += cal2(u , v) ;
int res2 = c[v] - d[u][v] ; //一个端点在v子树内部,另一个端点在u子树外部。
c[u] += res2 ;
int cc = p[u].size() - d[u][v] ;
res += 1ll * res2 * cc ;
}
return res ;
}
int main()
{
std::ios::sync_with_stdio(false) , cin.tie(0) ;
cin >> n ;
for(int i = 1 ; i <= n - 1 ; i ++)
{
int u , v ;
cin >> u >> v ;
g[u].push_back(v) ;
g[v].push_back(u) ;
}
vector tmp ;
dfs1(1 , 1 , 1) ;
cin >> m ;
for(int i = 1 ; i <= m ; i ++)
{
int u , v ;
cin >> u >> v ;
int lc = lca(u , v) ;
if(u == v) p[u].push_back({-1 , -1}) ;
else if(u == lc)
{
c[v] ++ ;
tmp.push_back(v) ;
p[lc].push_back({change(lc , v) , -1}) ;
}
else if(v == lc)
{
c[u] ++ ;
tmp.push_back(u) ;
p[lc].push_back({change(lc , u) , -1}) ;
}
else
{
c[u] ++ ;
c[v] ++ ;
tmp.push_back(u) ;
tmp.push_back(v) ;
int t1 = change(lc , u) ;
int t2 = change(lc , v) ;
p[lc].push_back({min(t1 , t2) , max(t1 , t2)}) ;
}
}
long long ans = 0 ;
ans += cal1() ;
ans += cal2(1 , 1) ;
for(auto u : tmp) ans += p[u].size() ;
cout << ans << '\n' ;
return 0 ;
}