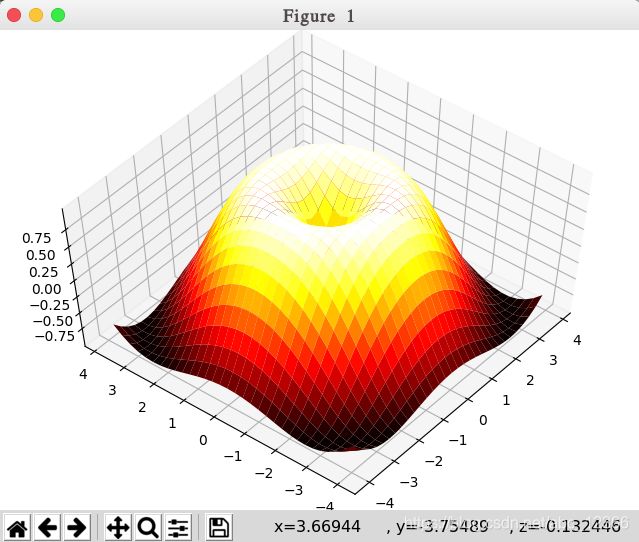
用Matplotlib做数据可视化（二）：绘制正弦曲线和等高线图 + 曲面图初步

也许，Matplotlib 是 Python 下使用最广泛的 2D 绘图工具库。
本文将用到 >>> numpy 库 <<< ，它是是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，是一个十分重要的 Python 第三方库。使用下面的命令进行安装。

sudo pip install numpy

import numpy as np

在使用前，允许我先对 numpy 进行简单的介绍。（如果你对此很熟悉可以选择跳过）

• ndarry 对象：存放同类型数据的 n 维数组对象。

  接受一个 “类数组” 的对象作为参数，“类数组” 如列表、元祖类型。

>>> a = np.array([1,2,3])

注意是接受 “一个”，如果是多维数组则要用括号括起来（[] 或者 () 都可）

>>> a = np.array([[1,2,3],[4,5,6]])
>>> a
array([[1, 2, 3],
       [4, 5, 6]])

len 函数返回传入对象的 “长度”，这里 ndarray 的长度就是它的维数（下面是一个三维数组）

>>> a = np.array([[1,2,],[4,5,],[7,8,]])
>>> a
array([[1, 2],
       [4, 5],
       [7, 8]])
>>> len(a)
3

• dtype：数据类型对象，使用 dtype 参数指定数据类型对象

# object：要转换成的数据类型
# align：若为true，填充字段使其类似C语言的结构体
# copy：复制dtype对象，若为false则只是复制内置数据类型对象的引用
numpy.dtype(object, align, copy)

记住，dtype返回的是数据类型对象（关于数据类型的 “对象”）

# int8, int16, int32, int64 四种数据类型可以使用字符串 'i1', 'i2','i4','i8' 代替
>>> dt = np.dtype('i4')
>>> dt
dtype('int32')

如果是结构化数据类型必须外面用方括号括起来，看下面两行表达式

student = np.dtype([('name','S20'), ('age', 'i1'), ('marks', 'f4')]) 
a = np.array([('abc', 21, 50),('xyz', 18, 75)], dtype = student)

# 1.student 是 numpy.dtype 类型，实际上是一个用户自定义的结构化数据。
# 2. a 是 numpy.ndarray 类型，共有两个维度（一个两行三列的矩阵）
# dtype 对于类型的作用效果是按列来的，即 'name' 对应着 'abc' 和 'xyz' 两行对象的数据

用下面这张表格更容易理解，理解后再看下面的终端交互部分

name（类型：S20）	age（类型：i1）	marks（类型：f4）
abc	21	50
xyz	18	75

>>> type(a)
<class 'numpy.ndarray'>
>>> type(a[0])
<class 'numpy.void'>
>>> type(a[0][1])
<class 'numpy.int8'>
>>> type(a[0]['age'])
<class 'numpy.int8'>

将数据类型应用于 ndarray 对象（作为 ndarray 的初始化函数之参数传入）

>>> dt = np.dtype([('age',np.int8)]) 
>>> a = np.array([(10,),(20,),(30,)], dtype = dt) 
>>> a
>>> array([(10,), (20,), (30,)], dtype=[('age', 'i1')])

>>> len(a)
3
>>> type(a)
<class 'numpy.ndarray'>
>>> type(a[0])
<class 'numpy.void'>  # void类型用于可变的自定义数据类型（相当于多种基本类型之结合）
>>> type(a[0][0])
<class 'numpy.int8'>

>>> a['age']  # 类型字段名可以用于存取实际的 age 列
array([10, 20, 30], dtype=int8)
>>> print(a['age'])
[10 20 30]

有关 Python 的 Numpy 模块，我将在后面用一篇博文进行讲解。上面这些知识应付本文已经足够。

绘制正弦函数和余弦函数图像

正弦函数和余弦函数，初中生都懂的东西。
说到底不论 sin 还是 cos 都是普通函数，Matplotlib 也没有给出额外的函数专门画它们的图像，对此我们使用通用的绘图函数 plot()

import numpy as np
import matplotlib.pyplot as plt

X = np.linspace(-np.pi, np.pi, 256)  # linspace是取点函数，在正负π之间取256个点
C, S = np.cos(X), np.sin(X)

plt.plot(X,C)  # 分别对应 x 方向和 y 方向
plt.plot(X,S)

plt.show()

绘制等高线图

对于高中学文的同学，等高线是地理必学。
它的巧妙之处在于，“二维输入，一维输出”。在平整四方的画布（电脑屏幕）上表示出二维的东西。

$f(x,y)=x^3+y^5-y^2$

要你画它的三维图像，直接画不好画可以借鉴等高线图的思路，将三维投射到二维平面（等间距向下投影）。

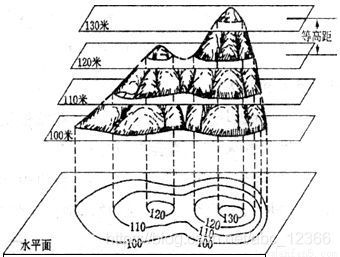
等高线属于高级图像，直接 plot 不了，在 Matplotlib 中有一个专门画等高线的函数，名曰 contourf()，这是一个高阶函数，它除了传入 x 方向和 y 方向外，还要传入一个额外的函数作为第三个参数（记住，等高线描述的对象是高维的，所以仅有 x 和 y 是无法确定作图的）

初次学习，重点掌握前三个参数（实际上也就多了一个函数参数）

contour([X, Y,] Z, [levels], **kwargs)

import numpy as np
import matplotlib.pyplot as plt

def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)  # 定义被描述的函数

n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)  # 对 x，y 数组进行扩充，生成网格点坐标矩阵，此行代码必不可少

plt.contourf(X, Y, f(X,Y), 8, alpha=.75, cmap='jet')
C = plt.contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
plt.show()

小明问：上面提到的 “生成网格点”，“网格点” 是个什么鬼？= =||
答曰：想象一个正六面体，就以魔方为例，每两个点的交汇处就是网格点，描述这些网格点的坐标的矩阵，就是坐标矩阵。

将二维图像三维化（Axes3D）

将二维图像三维化，主要用到 Matplotlib 工具包中的一个 3D 类库 Axes3D
使用起来也很简单，只要两行代码。（如果你像我一样写）

from mpl_toolkits.mplot3d import Axes3D
ax = Axes3D(plt.figure())

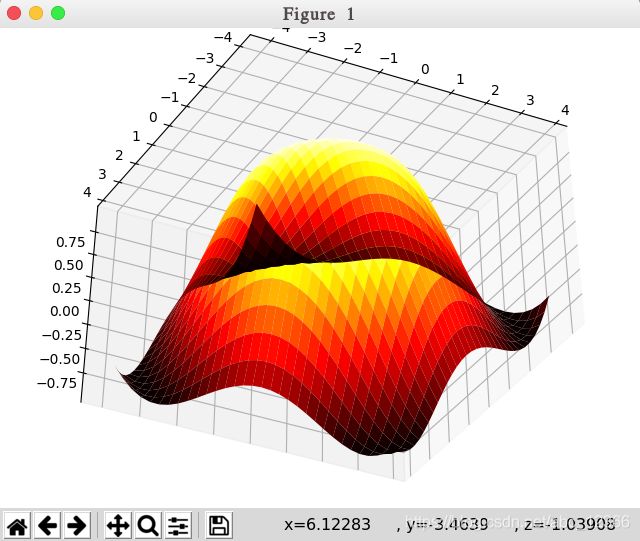
以下是前两个示例的 3D 版本

最后贴一份代码，你自己去研究罢

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot')

plt.show()

小结：上一节我们学会了用 Matplotlib 如何绘制基本的折线、条形、块状和饼状图，通过本文的学习我们又学会了如何绘制基本函数（本文是正弦，普通函数将表达式换一下即可换汤不换药）；最后我还附赠了你一个绘制平面三维图形的实用方法。好，就这样了，下节我们继续探讨，届时还将补充一些你不知道的细节，敬请期待！