【SRP协议】The Secure Remote Password Protocol论文笔记
The Secure Remote Password Protocol
作者:Thomas Wu
发表:NDSS 1998
一、非对称密钥交换(AKE)
在介绍本文重点的SRP协议之前,首先先要从宏观的角度上介绍非对称密钥交换这种技术。
-
特点:AKE不需要加密任何协议数据流。可以抽象地理解为,交换密钥的双方互相共享一部分信息,然后利用共享的信息以及自己本身所具有的秘密可以得到一样的密钥,也就成为了他们之间唯一的会话密钥。具体地细节要通过具体协议和数学公式去理解。
-
优点:
- 简化协商加密算法的过程
- 避免加密算法本身脆弱性的影响
- 避免了加密算法使用权等问题
-
等式要求:从数学层面上讲,AKE协议应当满足以下数学等式的要求
( ∀ w , x , y , z ) S ( R ( P ( w ) , P ( x ) ) , Q ( y , z ) ) = S ( R ( P ( y ) , P ( z ) ) , Q ( w , x ) ) (\forall w,x,y,z)\ S(R(P(w),P(x)),Q(y,z))=S(R(P(y),P(z)),Q(w,x)) (∀w,x,y,z) S(R(P(w),P(x)),Q(y,z))=S(R(P(y),P(z)),Q(w,x))
其中w,x,y,z属于任意的参数;P(x)为单向验证生成函数;Q(x,y),R(x,y)公开、私有参数的混合参数;S(x,y)会话密钥生成函数;K会话密钥 -
协议交互:x和z属于Carol和Steve的长期秘密,在真实的协议中往往相当于口令,由Carol发给Steve P(x),Steve发给Carol P(z),此后再交换临时秘密w和y,生成会话密钥。
二、SRP:AKE的一种实施
(一)SRP定义规则
- 所有计算都在有限域GF(n)中进行
- P ( ) : P ( x ) = g x m o d n P():P(x)=g^x\ mod\ n P():P(x)=gx mod n
- Q ( ) : Q ( w , x ) = w + u x Q():Q(w,x)=w+ux Q():Q(w,x)=w+ux
- R ( ) : R ( w , x ) = w x u R():R(w,x)=wx^u R():R(w,x)=wxu
- S ( ) : S ( w , x ) = w x S():S(w,x)=w^x S():S(w,x)=wx
其中 u = f ( w , x ) u=f(w,x) u=f(w,x)
(二)SRP协议
其中 C C C代表用户名, v = g x v=g^x v=gx, S = g a b + b u x S=g^{ab+bux} S=gab+bux
数学符合的含义一览
- n:大素数,模数
- g:模n的原根(又称为生成元)
- s:一个随机字符串用作盐值
- P:用户的口令
- x:由P和s生成的私钥
- v:主机的口令验证器
- u:随机拼凑的参数,公开揭示
- a,b:临时的密钥,随机生成且不公开
- A,B:相关公钥
- H():单向哈希函数
- m,n:逗号表示对m和n两个字符串进行串联
- K:会话密钥
解释一下协议,Carol首先将自己的用户名发送给Steve,Steve(一般指服务器)可以从自己的用户注册目录中找到该用户名对应的盐值s和口令验证器v。此后将盐值发送给Carol,Carol收到盐值后结合自己的口令P生成私钥x,然后利用私钥a生成公钥A发送给Steve,Steve同样生成公钥 g b g^b gb并用v保护起来得到B,并结合一个公开参数u一同发送给Carol(这里就体现了AKE协议的特点,互相共享部分信息)。双方收到来自对方的共享信息后开始生成会话密钥,可以得到同样的会话密钥(读者可自行验算)。后一轮交互是挑战响应的验证过程,确保双方都得到了相同的密钥,这样就对身份完成了认证。
(三)SRP细节解释
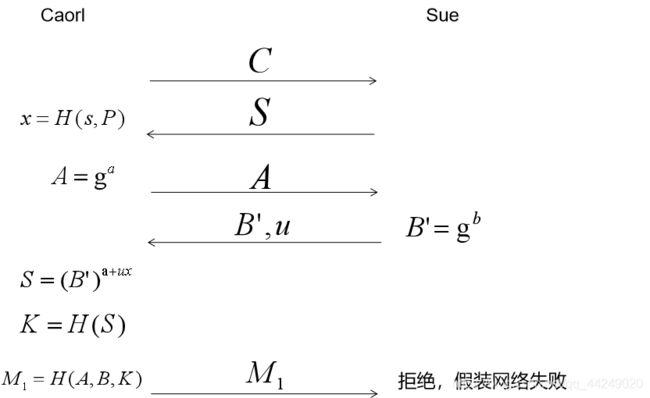
问题1 为什么发送 B = v + g b B=v+g^b B=v+gb而不是发送 B = g b B=g^b B=gb?
直接发送 B = g b B=g^b B=gb容易被字典攻击。如果攻击者Sue从合法会话中截获盐值s,可以进行下列步骤的攻击。
此时攻击者Sue拥有A,b,M1,开始猜测P,按顺序依次,算出x,算出v,算出S,算出K,算出M1,此时就可以拿已经掌握的M1和算出来的M1进行比对,从而实施字典攻击。
个人理解就是Sue在原版的SRP协议中,如果想实施字典攻击,Sue缺少验证文本(Sue很难得到一个正确的验证文本),而一旦 B = g b B=g^b B=gb就会让Sub通过交互得到正确的验证文本,从而可以实现攻击。
问题2 那么B应当如何保护v?
SRP是AKE的一种实现,实现方式可以不止这一种,但是基本的思路是不变的。B中应当选取适当的f()函数以保护v,避免v的泄露导致攻击者得到验证文本从而进行字典攻击。
- 避免 B = f ( v , g b ) B=f(v,g^b) B=f(v,gb)中的f()会满足条件 f ( g x , g y ) = g f ′ ( x , y ) f(g^x,g^y)=g^{f'(x,y)} f(gx,gy)=gf′(x,y),其中 f ′ ( x , y ) f'(x,y) f′(x,y)是一个很简单的派生,比如 f ( x , y ) = x y f(x,y)=xy f(x,y)=xy就属于 f ( g x , g y ) = g x + y f(g^x,g^y)=g^{x+y} f(gx,gy)=gx+y,一旦有这种性质,攻击者便可以将其利用。
- 尽量减少信息泄露,避免被分区攻击,不使用 f ( x , y ) = x ⊕ y f(x,y)=x\oplus y f(x,y)=x⊕y, f ( x , y ) = E y ( x ) f(x,y)=E_y(x) f(x,y)=Ey(x),结果可以排除大于n的
- g也必须要求是原根,否则可能会被分区攻击
问题3 u的作用是什么?
u可以确保不会被轻易仿冒,可以将认证的信息加入到会话并生成会话密钥。
u一定不可以在Steve得到A之前公开,可以是u由B生成得到,u也不能为0.
如果Chris可以提前得到了u的话,Chris一旦捕获到了v的值,那么即使其没有口令P,Chris可以实施新的攻击
三、安全性分析
(一)安全性要求
- 口令P和私钥x在成功的通信中不能泄露
- 会话密钥K在成功的通信中不能泄露
- 攻击者伪造变造消息的行为并不会让其成功通信或得到有用的信息
- 即使攻击者得到了v,他也只能通过复杂的字典搜索才能伪造用户身份
- 过去的会话密钥被攻击不会使得攻击者得到用户的口令
- 如果用户口令被攻击,攻击者不能决定过去的密钥或解密它
(二)SRP的安全性高于Diffie-Hellman
通过分析两个协议中的Q()函数可以利用归约证明结论。
SRP的Q()函数, Q ( g a , g b + g x , u , g , n , x ) = g a b + b u x Q(g^a,g^b+g^x,u,g,n,x)=g^{ab+bux} Q(ga,gb+gx,u,g,n,x)=gab+bux
DH的Q’()函数, Q ′ ( g a , g b , g , n ) = g a b Q'(g^a,g^b,g,n)=g^{ab} Q′(ga,gb,g,n)=gab
SRP的Q()函数可以表示DH的Q’()函数, Q ′ ( A , B , g , n ) = Q ( A , B + g n − 1 2 , 2 , g , n , n − 1 2 ) Q'(A,B,g,n)=Q(A,B+g^{\frac{n-1}{2}},2,g,n,\frac{n-1}{2}) Q′(A,B,g,n)=Q(A,B+g2n−1,2,g,n,2n−1)
(三)抵抗Denning-Sacco攻击
Denning-Sacco攻击:攻击者窃听到会话密钥K,然后得到伪造成用户或对口令进行暴力破解的能力
SRP协议中,攻击者得到K只能顺势算出来M1,M2(归功于单向哈希函数),没法利用其进行字典攻击。
(四)抵抗主动攻击
SRP可以抵抗大多数常见的攻击,可以抵抗中间人攻击,攻击者不知道x的话就没办法骗Steve,不知道v的话就无法欺骗Carol。
(五)安全假设与限制
-
离散对数
P ( x ) = g x P(x)=g^x P(x)=gx离散对数的难解性
-
群参数约定
n是non-smooth素数,即n-1也不能有小因子
n是安全素数,即n=2p+1,p也为素数,这样的条件可以抵抗小子群限制攻击
如何分配好参数:
- server把n和g在协议中发送给client——灵活,易变
- 参数嵌入到双端的系统软件中——避免被测试临时参数
-
限制检测
用户和服务端都应该对于参数的安全性进行检测
n是一个安全大素数(用户端)
g是GF(n)的原根(用户端)
A≠0(服务端)
B≠0(用户端)
a , b > l o g g n a,b\gt log_gn a,b>loggn 避免直接求对数就可以得到结果
四、优化SRP
(一)影响效率的因素
- 通信轮数
- 交换信息的字节大小
- 正常的执行时间
(二)两轮优化
合并没有前后依赖的消息
- C ⇒ S : C , A C\Rightarrow S:C,A C⇒S:C,A
- S ⇒ C : s , B S\Rightarrow C:s,B S⇒C:s,B
- C ⇒ S : M 1 C\Rightarrow S:M_1 C⇒S:M1
- S ⇒ C : M 2 S\Rightarrow C:M_2 S⇒C:M2
(三)一轮半优化
只单向认证
- C ⇒ S : C , A C\Rightarrow S:C,A C⇒S:C,A
- S ⇒ C : s , B S\Rightarrow C:s,B S⇒C:s,B
- C ⇒ S : M 1 C\Rightarrow S:M_1 C⇒S:M1
注意:一轮协议是很危险的,容易被重放攻击
(四)执行时间
群运算是最耗费时间的
SRP中的 g a g^a ga和 g b g^b gb都是可以提前计算的