模型预测控制系列(MPC)系列:1.建立车辆横向动力学模型
Hi All
新年挖新坑,今日开启船新连载.内容是无人车的横向控制,整体涵盖从0-1为车辆横向控制设计MPC控制器设计与MPC+MRAC耦合控制.大家有问题,有兴趣可以在评论区多多交流.
车辆横向动力学模型
引言
首先我们要问:针对车辆横向控制的问题,我们为什么需要建立动力学模型?
简单来说,当车辆在较高速度下行驶时,运动学模型(自行车模型)中提出"汽车轮胎速度方向与车辆朝向相同"的假设不再成立.车辆受到的横向力将不可忽视,如向心力将随着速度的增大而平方倍地增大.因此引入动力学模型,旨在建立更高阶量之间的联系,以更好地描述车辆转弯的非线性特性.
那么,让我们开始吧.为了在不失一般性的前提下尽可能简化模型,动力学模型将建立在以下几个假设上
1.轮胎速度方向与车辆纵向方向( x )的夹角 θ v (后统称轮胎速度方向角)较小且满足小角度假设: a ) θ v ≈ t a n θ v 2.轮胎转角( δ )与轮胎速度方向角( θ v )的夹角 α (后统称轮胎侧滑角)较小 3.车辆纵向速度维持不变: a ) V x : = C o n s t a n t 4.忽略路堤角( ϕ )对横向控制的影响 \begin{aligned} &\text{1.轮胎速度方向与车辆纵向方向($x$)的夹角$\theta_v$(后统称轮胎速度方向角)较小且满足小角度假设:}\\ &\qquad a) \ \theta_v \approx tan\theta_v \\ &\text{2.轮胎转角($\delta$)与轮胎速度方向角($\theta_v$)的夹角$\alpha$(后统称轮胎侧滑角)较小} \\ &\text{3.车辆纵向速度维持不变:} \\ &\qquad a) \ V_x : = Constant \\ &\text{4.忽略路堤角($\phi$)对横向控制的影响} \end{aligned} 1.轮胎速度方向与车辆纵向方向(x)的夹角θv(后统称轮胎速度方向角)较小且满足小角度假设:a) θv≈tanθv2.轮胎转角(δ)与轮胎速度方向角(θv)的夹角α(后统称轮胎侧滑角)较小3.车辆纵向速度维持不变:a) Vx:=Constant4.忽略路堤角(ϕ)对横向控制的影响
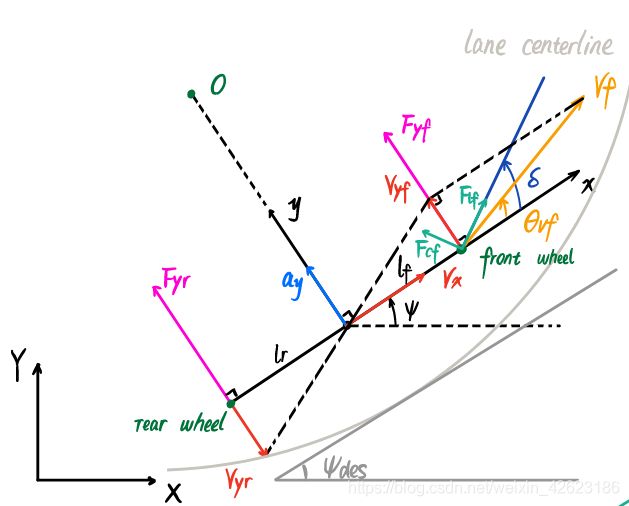
坐标系
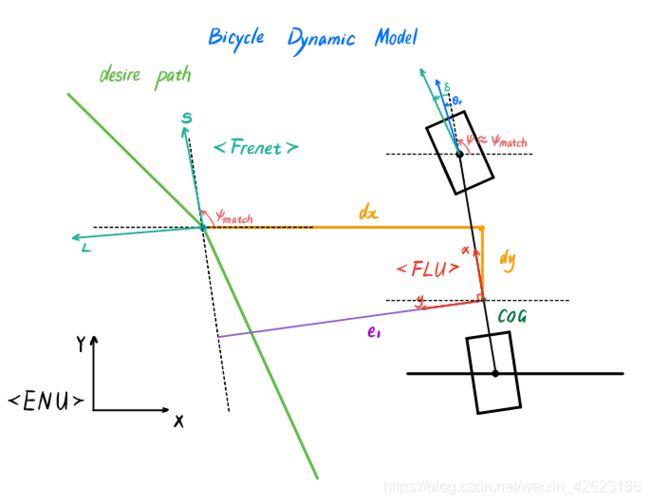
本模型在 F L U (Front-Left-Universe) FLU \text{(Front-Left-Universe)} FLU(Front-Left-Universe) 惯性坐标系下建立.坐标系原点固定在车辆质心位置, x x x轴方向为车辆纵向方向,指向车头前方. y y y轴方向与x轴垂直且指向车辆左侧, z z z轴方向垂直于 x x x, y y y轴且指向天空.值得注意的是,全局(地图)坐标系为ENU(East-North-Universe),其xyz指向规则于FLU相似,分别指向东北天.还有一个局部坐标系为Frenet坐标系,其固定在理想轨迹上,这里就不展开讲了,详见下图.
受力分析
根据牛顿第二定律,对车辆y方向(横向)进行受力分析
F y f + F y r = m a y F_{yf} + F_{yr} = ma_y Fyf+Fyr=may
其中 F y f F_{yf} Fyf 与 F y r F_{yr} Fyr 分别是车辆前轮和后轮在 y y y方向受到的力, m m m为车辆质量, a y a_y ay为车辆在 y y y方向上的加速度.
车辆在 y y y方向上的加速度由两部分构成:
1.因车辆在 y y y方向上运动产生的加速度,定义为 y ¨ \ddot{y} y¨.
2.车辆的向心加速度,记为 a y c a_{yc} ayc.
a y = y ¨ + a y c = y ¨ + ω 2 R = y ¨ + ψ ˙ 2 R = y ¨ + V x ψ ˙ a_y = \ddot{y}+a_{yc} = \ddot{y}+\omega^2R = \ddot{y}+\dot{\psi}^2R = \ddot{y}+V_x\dot{\psi} ay=y¨+ayc=y¨+ω2R=y¨+ψ˙2R=y¨+Vxψ˙
因此
F y f + F y r = m ( y ¨ + V x ψ ˙ ) F_{yf} + F{yr} = m(\ddot{y}+V_x\dot{\psi}) Fyf+Fyr=m(y¨+Vxψ˙)
对z轴进行偏航动力学分析,由力矩平衡可得
I z ψ ¨ = l f F y f − l r F y r I_z\ddot{\psi}=l_fF_{yf} - l_rF_{yr} Izψ¨=lfFyf−lrFyr
其中 l f l_f lf 与 l r l_r lr 分别是车辆前轮和后轮距离车辆重心的距离.
下一步,我们要对横向力 F y f F_{yf} Fyf 与 F y r F_{yr} Fyr 进行分析.实验表明,当轮胎侧滑角 α \alpha α 较小时,轮胎受到的横向力的大小与轮胎侧滑角成正比.其中轮胎侧滑角被定义为轮胎转角与轮胎速度方向角的夹角.
因此,前轮(方向轮)侧滑角 α f \alpha_f αf 为
α f = δ − θ v f \alpha_f = \delta - \theta_{vf} αf=δ−θvf
其中 δ \delta δ为前轮转角, θ v f \theta_{vf} θvf 为前轮速度方向角.
同理,后轮(假定后轮无法转向)侧滑角为
α r = 0 − θ v r = − θ v r \alpha_r = 0 - \theta_{vr} = - \theta_{vr} αr=0−θvr=−θvr
其中 θ v r \theta_{vr} θvr 为后轮速度方向角.
基于上述两点推断, 轮胎横向力可被改写为以下形式
F y f = 2 C α f ( δ − θ v f ) F y r = − 2 C α r θ v r \begin{aligned} &F_{yf} = 2C_{\alpha_f}(\delta - \theta_{vf}) \\ &F_{yr} = -2C_{\alpha_r}\theta_{vr} \end{aligned} Fyf=2Cαf(δ−θvf)Fyr=−2Cαrθvr
其中 C α f C_{\alpha_f} Cαf 与 C α r C_{\alpha_r} Cαr 分别为前轮与后轮的侧滑刚度系数.
由小角度假设与牵连运动公式可得
θ v f ≈ t a n ( θ v f ) = y ˙ + l f ψ ˙ V x θ v r ≈ t a n ( θ v r ) = y ˙ − l r ψ ˙ V x \begin{aligned} &\theta_{vf} \approx tan(\theta_{vf}) = \frac{\dot{y} + l_f\dot{\psi}}{V_x} \\ &\theta_{vr} \approx tan(\theta_{vr}) = \frac{\dot{y} - l_r\dot{\psi}}{V_x} \end{aligned} θvf≈tan(θvf)=Vxy˙+lfψ˙θvr≈tan(θvr)=Vxy˙−lrψ˙
综上可得
y ¨ = 2 m [ C α f δ − C α f + C α r V x y ˙ + − C α f l f + C α r l r V x ψ ˙ ] − V x ψ ˙ ψ ¨ = 2 I z ( C α f l f δ − C α f l f − C α r l r V x y ˙ − C α f l f 2 + C α r l r 2 V x ψ ˙ ) \begin{aligned} &\ddot{y} = \frac{2}{m}[C_{\alpha_f}\delta - \frac{C_{\alpha_f}+C_{\alpha_r}}{V_x}\dot{y}+ \frac{-C_{\alpha_f}l_f+C_{\alpha_r}l_r}{V_x}\dot{\psi}] -V_x\dot{\psi} \\ &\ddot{\psi}=\frac{2}{I_z}(C_{\alpha_f}l_f\delta-\frac{C_{\alpha_f}l_f- C_{\alpha_r}l_r}{V_x}\dot{y}-\frac{C_{\alpha_f}l_f^2+C_{\alpha_r}l_r^2}{V_x}\dot{\psi}) \end{aligned} y¨=m2[Cαfδ−VxCαf+Cαry˙+Vx−Cαflf+Cαrlrψ˙]−Vxψ˙ψ¨=Iz2(Cαflfδ−VxCαflf−Cαrlry˙−VxCαflf2+Cαrlr2ψ˙)
将上式改写为矩阵形式
[ y ˙ y ¨ ψ ˙ ψ ¨ ] = [ 0 1 0 0 0 − 2 ( C α f + C α r ) m V x 0 2 ( − C α f l f + C α r l r ) m V x − V x 0 0 0 1 0 − 2 ( C α f l f − C α r l r ) I z V x 0 − 2 ( C α f l f 2 + C α r l r 2 ) I z V x ] [ y y ˙ ψ ψ ˙ ] + [ 0 2 C α f m 0 2 C α f l f I z ] δ \begin{bmatrix} \dot{y} \\ \ddot{y} \\ \dot{\psi} \\ \ddot{\psi} \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{2(C_{\alpha_f}+C_{\alpha_r})}{mV_x} & 0 & \frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}-V_x \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{2(C_{\alpha_f}l_f- C_{\alpha_r}l_r)}{I_zV_x} & 0 & -\frac{2(C_{\alpha_f}l_f^2+C_{\alpha_r}l_r^2)}{I_zV_x} \\ \end{bmatrix} \begin{bmatrix} y \\ \dot{y} \\ \psi \\ \dot{\psi} \\ \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{2C_{\alpha_f}}{m} \\ 0 \\ \frac{2C_{\alpha_f}l_f}{I_z} \\ \end{bmatrix} \delta ⎣⎢⎢⎡y˙y¨ψ˙ψ¨⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001−mVx2(Cαf+Cαr)0−IzVx2(Cαflf−Cαrlr)00000mVx2(−Cαflf+Cαrlr)−Vx1−IzVx2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤⎣⎢⎢⎡yy˙ψψ˙⎦⎥⎥⎤+⎣⎢⎢⎢⎡0m2Cαf0Iz2Cαflf⎦⎥⎥⎥⎤δ
动力学误差模型
将动力学模型中的状态变量设置为误差量,将有利于简化后续控制器的设计.因此,定义误差状态变量
e 1 : = y − y d e s 横向误差 e 2 : = ψ − ψ d e s 前轮航向角误差 \begin{aligned} &e_1:= y-y_{des} \quad\text{横向误差} \\ &e_2:= \psi-\psi_{des} \quad\text{前轮航向角误差} \\ \end{aligned} e1:=y−ydes横向误差e2:=ψ−ψdes前轮航向角误差
误差动力学分析
理想航向角速率
ψ ˙ d e s = V x R \dot{\psi}_{des} = \frac{V_x}{R} ψ˙des=RVx
理想横向加速度为
a y d e s = y ¨ d e s + a y c d e s = 0 + V x 2 R = V x ψ ˙ d e s a_{y_{des}} = \ddot{y}_{des}+a_{yc_{des}} = 0+\frac{V^2_x}{R} = V_x\dot{\psi}_{des} aydes=y¨des+aycdes=0+RVx2=Vxψ˙des
因此,横向误差 e 1 e_1 e1可改写为
e ¨ 1 = a y − a y d e s = y ¨ + V x ψ ˙ − V x ψ ˙ d e s = y ¨ + V x ( ψ ˙ − ψ ˙ d e s ) = y ¨ + V x e ˙ 2 \ddot{e}_1 = a_y - a_{y_{des}} = \ddot{y}+V_x\dot{\psi}-V_x\dot{\psi}_{des} = \ddot{y}+V_x(\dot{\psi}-\dot{\psi}_{des}) = \ddot{y}+V_x\dot{e}_2 e¨1=ay−aydes=y¨+Vxψ˙−Vxψ˙des=y¨+Vx(ψ˙−ψ˙des)=y¨+Vxe˙2
前面提到 V x V_x Vx为常数,因此对上式积分可得
e ˙ 1 = y ˙ + V x ( ψ − ψ d e s ) = y ˙ + V x e 2 \dot{e}_1 = \dot{y}+V_x(\psi-\psi_{des}) = \dot{y}+V_xe_2 e˙1=y˙+Vx(ψ−ψdes)=y˙+Vxe2
由此可得
y ˙ = e ˙ 1 − V x e 2 y ¨ = e ¨ 1 − V x e ˙ 2 ψ ˙ = ψ ˙ d e s + e ˙ 2 \begin{aligned} & \dot{y} = \dot{e}_1 - V_xe_2\\ & \ddot{y} = \ddot{e}_1 - V_x\dot{e}_2 \\ & \dot{\psi}= \dot{\psi}_{des}+\dot{e}_2 \\ \end{aligned} y˙=e˙1−Vxe2y¨=e¨1−Vxe˙2ψ˙=ψ˙des+e˙2
将上述式子代入到动力学模型中,替换掉原先的变量可得
( e ¨ 1 − V x e ˙ 2 ) = 2 m [ C α f δ − C α f + C α r V x ( e ˙ 1 − V x e 2 ) + − C α f l f + C α r l r V x ( ψ ˙ d e s + e ˙ 2 ) ] − V x ( ψ ˙ d e s + e ˙ 2 ) ψ ¨ = 2 I z ( C α f l f δ − C α f l f − C α r l r V x ( e ˙ 1 − V x e 2 ) − C α f l f 2 + C α r l r 2 V x ( ψ ˙ d e s + e ˙ 2 ) ) \begin{aligned} &(\ddot{e}_1 - V_x\dot{e}_2) = \frac{2}{m}[C_{\alpha_f}\delta - \frac{C_{\alpha_f}+C_{\alpha_r}}{V_x}(\dot{e}_1 - V_xe_2)+ \frac{-C_{\alpha_f}l_f+C_{\alpha_r}l_r}{V_x}(\dot{\psi}_{des}+\dot{e}_2)] -V_x(\dot{\psi}_{des}+\dot{e}_2) \\ &\ddot{\psi}=\frac{2}{I_z}(C_{\alpha_f}l_f\delta-\frac{C_{\alpha_f}l_f- C_{\alpha_r}l_r}{V_x}(\dot{e}_1 - V_xe_2)-\frac{C_{\alpha_f}l_f^2+C_{\alpha_r}l_r^2}{V_x}(\dot{\psi}_{des}+\dot{e}_2)) \end{aligned} (e¨1−Vxe˙2)=m2[Cαfδ−VxCαf+Cαr(e˙1−Vxe2)+Vx−Cαflf+Cαrlr(ψ˙des+e˙2)]−Vx(ψ˙des+e˙2)ψ¨=Iz2(Cαflfδ−VxCαflf−Cαrlr(e˙1−Vxe2)−VxCαflf2+Cαrlr2(ψ˙des+e˙2))
整理可得
e ¨ 1 = 2 C α f m δ + − 2 ( C α f + C α r ) m V x e ˙ 1 + 2 ( C α f + C α r ) m e 2 + 2 ( − C α f l f + C α r l r ) m V x e ˙ 2 + ( 2 ( − C α f l f + C α r l r ) m V x − V x ) ψ ˙ d e s ψ ¨ = 2 C α f l f I z δ + − 2 ( C α f l f − C α r l r ) I z V x e ˙ 1 + 2 ( C α f l f − C α r l r ) I z e 2 + − 2 ( C α f l f 2 + C α r l r 2 ) I z V x e ˙ 2 + − 2 ( C α f l f 2 + C α r l r 2 ) I z V x ψ ˙ d e s \begin{aligned} &\ddot{e}_1 = \frac{2C_{\alpha_f}}{m}\delta+\frac{-2(C_{\alpha_f}+C_{\alpha_r})}{mV_x}\dot{e}_1 +\frac{2(C_{\alpha_f}+C_{\alpha_r})}{m}e_2 + \frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}\dot{e}_2 +(\frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}-V_x)\dot{\psi}_{des} \\ &\ddot{\psi} = \frac{2C_{\alpha_f}l_f}{I_z}\delta+\frac{-2(C_{\alpha_f}l_f-C_{\alpha_r}l_r)}{I_zV_x}\dot{e}_1 +\frac{2(C_{\alpha_f}l_f-C_{\alpha_r}l_r)}{I_z}e_2 +\frac{-2(C_{\alpha_f}l^2_f+C_{\alpha_r}l^2_r)}{I_zV_x}\dot{e}_2 +\frac{-2(C_{\alpha_f}l^2_f+C_{\alpha_r}l^2_r)}{I_zV_x}\dot{\psi}_{des} \end{aligned} e¨1=m2Cαfδ+mVx−2(Cαf+Cαr)e˙1+m2(Cαf+Cαr)e2+mVx2(−Cαflf+Cαrlr)e˙2+(mVx2(−Cαflf+Cαrlr)−Vx)ψ˙desψ¨=Iz2Cαflfδ+IzVx−2(Cαflf−Cαrlr)e˙1+Iz2(Cαflf−Cαrlr)e2+IzVx−2(Cαflf2+Cαrlr2)e˙2+IzVx−2(Cαflf2+Cαrlr2)ψ˙des
改写为矩阵形式
[ e ˙ 1 e ¨ 1 e ˙ 2 e ¨ 2 ] = [ 0 1 0 0 0 − 2 ( C α f + C α r ) m V x 2 ( C α f + C α r ) m 2 ( − C α f l f + C α r l r ) m V x 0 0 0 1 0 − 2 ( C α f l f − C α r l r ) I z V x 2 ( C α f l f − C α r l r ) I z − 2 ( C α f l f 2 + C α r l r 2 ) I z V x ] [ e 1 e ˙ 1 e 2 e ˙ 2 ] + [ 0 2 C α f m 0 2 C α f l f I z ] δ + [ 0 2 ( − C α f l f + C α r l r ) m V x − V x 0 − 2 ( C α f l f 2 + C α r l r 2 ) I z V x ] ψ ˙ d e s \begin{bmatrix} \dot{e}_1 \\ \ddot{e}_1 \\ \dot{e}_2 \\ \ddot{e}_2 \\ \end{bmatrix}= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & \frac{-2(C_{\alpha_f}+C_{\alpha_r})}{mV_x} & \frac{2(C_{\alpha_f}+C_{\alpha_r})}{m} & \frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}\\ 0 & 0 & 0 & 1 \\ 0 & \frac{-2(C_{\alpha_f}l_f-C_{\alpha_r}l_r)}{I_zV_x} & \frac{2(C_{\alpha_f}l_f-C_{\alpha_r}l_r)}{I_z} & \frac{-2(C_{\alpha_f}l^2_f+C_{\alpha_r}l^2_r)}{I_zV_x} \\ \end{bmatrix} \begin{bmatrix} e_1 \\ \dot{e}_1 \\ e_2 \\ \dot{e}_2 \\ \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{2C_{\alpha_f}}{m} \\ 0 \\ \frac{2C_{\alpha_f}l_f}{I_z} \\ \end{bmatrix} \delta + \begin{bmatrix} 0 \\ \frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}-V_x \\ 0 \\ \frac{-2(C_{\alpha_f}l^2_f+C_{\alpha_r}l^2_r)}{I_zV_x} \\ \end{bmatrix} \dot{\psi}_{des} ⎣⎢⎢⎡e˙1e¨1e˙2e¨2⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001mVx−2(Cαf+Cαr)0IzVx−2(Cαflf−Cαrlr)0m2(Cαf+Cαr)0Iz2(Cαflf−Cαrlr)0mVx2(−Cαflf+Cαrlr)1IzVx−2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤⎣⎢⎢⎡e1e˙1e2e˙2⎦⎥⎥⎤+⎣⎢⎢⎢⎡0m2Cαf0Iz2Cαflf⎦⎥⎥⎥⎤δ+⎣⎢⎢⎢⎡0mVx2(−Cαflf+Cαrlr)−Vx0IzVx−2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤ψ˙des
定义
x = [ e 1 e ˙ 1 e 2 e ˙ 2 ] A = [ 0 1 0 0 0 − 2 ( C α f + C α r ) m V x 2 ( C α f + C α r ) m 2 ( − C α f l f + C α r l r ) m V x 0 0 0 1 0 − 2 ( C α f l f − C α r l r ) I z V x 2 ( C α f l f − C α r l r ) I z − 2 ( C α f l f 2 + C α r l r 2 ) I z V x ] B = [ 0 2 C α f m 0 2 C α f l f I z ] B c = [ 0 2 ( − C α f l f + C α r l r ) m V x − V x 0 − 2 ( C α f l f 2 + C α r l r 2 ) I z V x ] \begin{aligned} &x = \begin{bmatrix} e_1 \\ \dot{e}_1 \\ e_2 \\ \dot{e}_2 \\ \end{bmatrix} \quad A = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & \frac{-2(C_{\alpha_f}+C_{\alpha_r})}{mV_x} & \frac{2(C_{\alpha_f}+C_{\alpha_r})}{m} & \frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}\\ 0 & 0 & 0 & 1 \\ 0 & \frac{-2(C_{\alpha_f}l_f-C_{\alpha_r}l_r)}{I_zV_x} & \frac{2(C_{\alpha_f}l_f-C_{\alpha_r}l_r)}{I_z} & \frac{-2(C_{\alpha_f}l^2_f+C_{\alpha_r}l^2_r)}{I_zV_x} \\ \end{bmatrix} \\ &B = \begin{bmatrix} 0 \\ \frac{2C_{\alpha_f}}{m} \\ 0 \\ \frac{2C_{\alpha_f}l_f}{I_z} \\ \end{bmatrix} \quad B_c = \begin{bmatrix} 0 \\ \frac{2(-C_{\alpha_f}l_f+C_{\alpha_r}l_r)}{mV_x}-V_x \\ 0 \\ \frac{-2(C_{\alpha_f}l^2_f+C_{\alpha_r}l^2_r)}{I_zV_x} \\ \end{bmatrix} \end{aligned} x=⎣⎢⎢⎡e1e˙1e2e˙2⎦⎥⎥⎤A=⎣⎢⎢⎢⎡00001mVx−2(Cαf+Cαr)0IzVx−2(Cαflf−Cαrlr)0m2(Cαf+Cαr)0Iz2(Cαflf−Cαrlr)0mVx2(−Cαflf+Cαrlr)1IzVx−2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤B=⎣⎢⎢⎢⎡0m2Cαf0Iz2Cαflf⎦⎥⎥⎥⎤Bc=⎣⎢⎢⎢⎡0mVx2(−Cαflf+Cαrlr)−Vx0IzVx−2(Cαflf2+Cαrlr2)⎦⎥⎥⎥⎤
则误差动力学方程为
x ˙ = A x + B δ + B c ψ ˙ d e s \dot{x} = Ax + B\delta + B_c\dot{\psi}_{des} x˙=Ax+Bδ+Bcψ˙des
离散化
离散化的方法有很多,例如双线性离散化,前向欧拉差分,后向欧拉差分,AB-2差分法等等.通常的,对于系统矩阵 A A A,为了保障其离散化后的精度与稳定性,我们采用双线性离散化的方法.对于控制矩阵 B B B与矩阵 B c B_c Bc,为了简化运算,我们采用前向欧拉差分法进行离散.离散后的结果如下:
A d = ( I − T 2 A ) − 1 ( I + T 2 A ) B d = B T B c d = B c T \begin{aligned} &A_d = (I-\frac{T}{2}A)^{-1}(I+\frac{T}{2}A)\\ &B_d = BT\\ &B_{cd} = B_cT \end{aligned} Ad=(I−2TA)−1(I+2TA)Bd=BTBcd=BcT
其中,下标 d d d表示离散域矩阵, T T T为离散时间
至此,我们完成了车辆横向动力学模型的搭建与离散化.下一步,就是将其封装为一个QP问题,并以此设计MPC控制器.