大规模文本相似性计算1(LSH理论部分)

  最近在做互联网热点发现时需要将全网一段时间内每一篇文章和它所有相关的报道聚集在一起形成一个事件，再对事件下报道的数量进行汇总和排序得到不同维度的热点事件。

  其中相关的报道定义为相似度较高的文章，相似度较高指的是文章间的关键词重合度超过一定阈值或者事件以及事件属性相似度超过一定阈值。

input :

60岁的穆罕默德在贾巴里亚难民营附近的家 中被火箭弹射杀

关键词:

穆罕默德:0.6198;贾巴里亚:0.5796;难民营:0.2304;火箭弹:0.2012;射杀:0.1718;附近:0.1701;60岁:0.1018;家中:0.0563;

事件:

  这其中涉及一个报道间两两计算相似度的问题。而一天内在各个网站，app，微博，微信等媒体文章的数量为4000万左右。假设一个报道取20个关键词，采用onehot编码，使用稀疏矩阵，两遍文章相似度计算复杂度为，其中，假设位置查找 + 对应位置加以及乘的计算量大约为100次。这样4000万篇文章两两计算复杂度为:

$(4\times 10^7{)}^2\times 1\times 10^2=1.6\times 10^{17}$

  现在计算及单核的计算速度为2ghz，即每秒钟20亿次浮点运算，这里还有操作系统占用资源以及程序调度，io等等占用的资源，真正用来计算的假设为单核2亿次($2\times 10^8$),那要完成这个计算任务，单核大约需要$8\times 10^8$秒，大约25年左右，即使加大投入10000核，理想状态下也需要1天来完成计算。

  所以这里需要一个策略能将时间复杂度由$O(N^2)$降为$O(N)$或者$O(NLogN)$。

  查询算法中最快的为哈希查询，能够在常数时间内找到具体的某一个物料。如果能将所有的物料按照其属性分到不同的块中，每个块中都是相似的文章，然后只计算块内元素的相似度，其计算量就能极大的简化了，就像哈希查找一样，通过一次哈希计算找到其相似文章所在的块，然后再逐个计算块内物料和查找文章相似度。如下图，假如分成10000个块。

  将4千万个报道平均分布在这1万个块中，每个块大约4千个报道，则总的计算量估计为

$(\frac{4\times 10^7}{10000}{)}^2\times 100\times 10000=1.6\times 10^{13}$

  同上单核计算能力为$2\times 10^8/s$大约需要$8\ast 10^4$秒，大约要22小时计算完，如果100核的集群，大约13分钟就能计算完。

  实际操作中全量数据并不是均匀分布在每个块上的，当一个块上数据量超过10万时，因为每一个块是单独计算的，多核并不能加快其计算，单块的计算时间为2小时，会拖慢整体任务进度。(实际使用中测试一个container中数量超过5万就会造成内存溢出)

  实际操作中也不是分为10000个块，一般使用$2^{32}-5$个块，具体原因在实现和参数设置篇描述。

  所以接下来的任务为，如何将全量数据中相似的项分到相同的块中，不相似的项分到不同的块中，且每块数据量均衡且不超过5万。

  分块的方式很多，如先按照报道的地域分块，再按照报道的领域分块，或者交叉分块，但是这种根据业务进行分块的方式一般为kdtree算法，但是并不能处理高纬度数据。

LSH的历史

  当前，在大规模高维数据集上近似最近邻问题最好的解决方案是位置敏感哈希，它将高维向量映射到低维空间，并且以较大的概率使映射前相近的映射后仍然相近。LSH虽然采用近似的方法，不保证得出精确的结果，但是它能以较低的代价返回精确的或接近精确的结果。LSH算法有多种，在不同度量空间及不同相似度量条件下有不同的方案。它们在多种场合得到应用，如计算生物学、音乐识别、图像检索、音乐检索、复制检测、近似重复检测和名词聚类等。

  LSH是由Indyk在斯坦福大学和他的导师Motwani 与1998年提出的，主要解决汉明空间的高维搜索问题。

  2004年，Datar、 Immorlica和 Indyk在斯坦福大学将p - 稳定分布函数引入LSH，并将LSH的使用范围扩展到欧氏空间。

  2005年，Indyk的学生Andoni给出了欧氏空间LSH具体实现方案，并称之为E2LSH。

  2008年，Andoni 在麻省理工大学将Leech lattice引入文献的LSH方案，将查询时间和内存消耗降到接近于文献中Motwani给出的下界。

  2010年，Andoni在他的博士论文中对LSH相关问题进行了详细描述。

Jaccard相似度

  判断两个集合是否相等，一般使用称之为Jaccard相似度的算法（后面用Jac(S1,S2)来表示集合S1和S2的Jaccard相似度）。举个列子，集合X = {a,b,c}，Y = {b,c,d}。那么Jac(X,Y) = 2 / 3 = 0.67。也就是说，结合X和Y有67%的元素相同。下面是形式的表述Jaccard相似度公式：

Jac(X,Y) = |X∩Y| / |X∪Y|

  也就是两个结合交集的个数比上两个集合并集的个数。
范围在[0,1]之间。

文档的局部敏感哈希算法

  此时如果我们有一种算法，能将两个文档$S_1$,$S_2$编码为一个数字$s_1$,$s_2$,文档相似的概率为这两个数字相等的概率。

  如果能得到上面的算法，就可对目标文档进行多次哈希处理，得到一个签名向量，所有的签名向量会形成签名矩阵M。再对签名分组进行哈希计算，使得相似项会比不相似项更可能哈西到同一桶中。然后将至少有一次哈希到同一桶中的文档对看成为候选对。我们只会检查这些候选对的相似度。这样哈希到同一个桶中的非相似文档称为伪正例(FP)，那些没有映射到相同桶中的真正相似的文档对称为伪反例(FN),我们希望FP和FN的都很小。

  我们将矩阵的行分成b个Band（r行为一个Band）

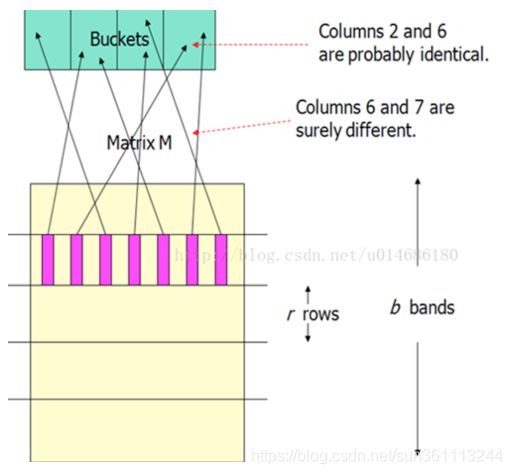
行条号策略分析

  假定使用b个行条，每个行条由r行组成，并假定某具体文档之间的jaccard相似度为s，上面已经说明某一种算法得到某个具体行中的两个签名相等的概率为s。接下来我们可以计算这些文档作为候选对的概率，具体计算过程如下：

1. 在某个具体行条中所有行的两个签名相等的概率为$s^r$

2. 在某个具体行条中至少有一对签名不相等的概率为$1-s^r$

3. 在任何行条中的任意一行的签名都不相等的概率为 $(1-s^r{)}^b$

4. 签名至少在一个行条中全部相等的概率，也就是称为候选对的概率为 $1-(1-s^r{)}^b$

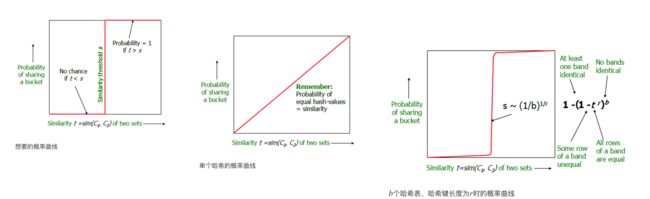
  虽然有可能并不特别明显，但是不论常数b和r的取值如何，上述形式的概率函数图像大致为下图给出的s曲线。曲线中上升最陡的地方对应的相似度就是所谓的阈值，他是b和r的函数。阈值是一个近似估计值为$(\frac{1}{b}{)}^{\frac{1}{r}}$,比如b=16, r=4 则阈值的近似度为0.5。

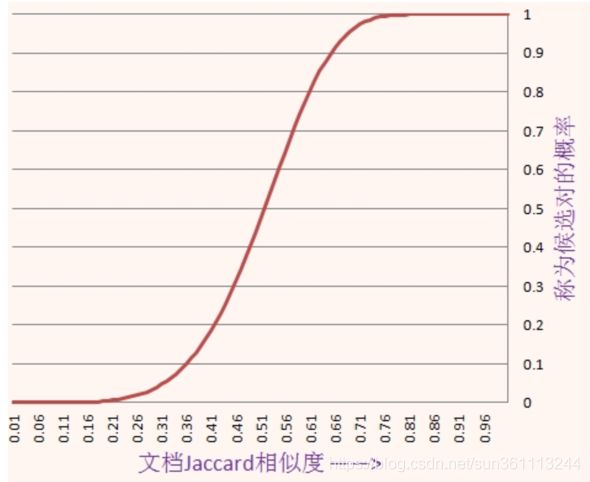
  考虑b=20且r=5的情况，也就是说假定签名的个数为100，分为20个行条，每个行条包含5行。于是两列成为候选对的概率为$1-(1-s^5{)}^{20}$不同相似度下它的采样值以及曲线如下

  当两篇文档的相似度为0.8时，它们hash到同一个桶而成为候选对的概率是0.9996，而当它们的相似度只有0.3时，它们成为候选对的概率只有0.0475，因此局部敏感hash解决了让相似的对以较高的概率hash到同一个桶，而不相似的项hash到不同的桶的问题。

集合的矩阵表示

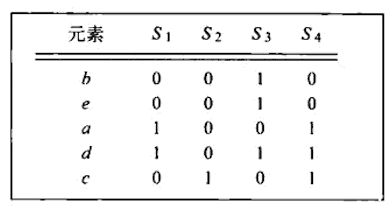
  假定给出全集{a , b, c, d , e}中元素组成的多个集合的矩阵表示，这里$S_1=\{a,d\}$,$S_2=\{c\}$,$S_3=\{b,d,e\}$,$S_4=\{a,c,d\}$，组成矩阵:

  实际中，数据不会存储为一个矩阵的一个原因是该矩阵往往非常稀疏(0的个数远远多于1的个数)，只存储1所在的位置能够大大节省存储的开销，同时又能完整的表示整个矩阵。

Minhash

  所谓的MinHsah，即进行如下的操作：

  1. 对$S_1,S_2,S_3,S_4$的n个维度，做一个随机排列（即对索引随机$a,b,c,d,e$打乱）

  2. 分别取向量$S_1,S_2,S_3,S_4$的第一个非0行的索引值（index），即为MinHash值

  举个例子,对上面的数据进行随机打乱，得到下图

  可以得到$h(S_1)=a,h(S_2)=c,h(S_3)=b,h(S_4)=a$

一个神奇的结论

$P(Minhash(S_1)=Minhash(S_2))=Jac(S_1,S_2)$

  在集合的jaccard相似度和最小哈希值之间存在着非同寻常的关联：

  两个集合经随机排列转换之后得到的两个最小哈希值相等的概率等于这两个集合的jaccard相似度。

  为了理解上述结论的原因，必须要对两个集合同一列所有可能的结果进行枚举，假设只考虑集合$S_1$和$S_2$所对应的列，那么他们所在的行可以按照所有可能的结果分为3类：

X类：两列的值均为1

Y类 : 其中一列值为0，另外一列为1

Z类：两列的值均为0

  由于特征非常稀疏，因此大部分行都属于Z类，但是X和Y类行的数目的比例决定了$Jac(S_1,S_2)$和概率$h(S_1)=h(S_2)$的大小，假定X类行的数目为x，Y类行的数目为y，则$Jac(S_1,S_2)=\frac{x}{x+y}$原因是$S_1\bigcup S_2$的大小为x，而$S_1\bigcap S_2$的大小为x+y。

  接下来考虑$h(S_1)=h(S_2)$的概率。设想所有行进行随机排列转换，然后从上到下进行扫描处理，在碰到Y类行之前碰到X类行的概率是$\frac{x}{x+y}$，如果从上往下扫描遇到的除Z类之外的第一行属于X类，那么肯定有$h(S_1)=h(S_2)$。另一方面，如果首先碰到的是Y类行，而不是Z类行，那么值为1的那个集合的最小哈希值为当前行。但值为0的那个集合必将会进一步扫描下去，因此，如果首先碰到Y类行，那么此时$h(S_1)\ne h(S_2)$.于是，可以得到最终结论，及$h(S_1)=h(S_2)$的概率为$\frac{x}{x+y}$

最小哈希签名

  之前用矩阵M表示特征矩阵，我们随机选择n个排列转换用于矩阵M的行处理，其中n一般为几百。对于集合S对应的列，分别调用这些排序转换锁具定的最小哈希函数$h_1,h_2,...h_n$则可构建S的最小哈希签名向量$h_1(S),h_2(S),...h_n(S)$,该向量通常写为列向量格式，因此，基于矩阵M可以构建一个签名矩阵，其中M的每一列替换为该列所对应的最小哈希签名向量即可。这里的签名矩阵与M的列数相同但行数只有n，通常签名矩阵所需要的空间比矩阵M本身需要的空间要小的多。

  对大规模特征矩阵进行行显示排列转换是不可行的，即使对上百万的行选择一个随机排列转换也及其消耗时间，而对行进行必要的排序则需要花费更多的时间，因此上面的算法理论上很吸引人，但是缺少可操作性。

  这里我们可以通过一个随机哈希函数来模拟随机排列转换的效果，该函数将行号映射到与行数目大致相等数量的桶中。通常，一个将整数0,1,…,k-1映射到桶号0,1,…,k-1的哈希函数会将某些整数映射到一个桶中，而有些桶却没有倍任何整数所映射到。然而，只要k很大且哈希结果冲突不太频繁的话，差异就不是很重要。于是，我们就可以继续假设哈希函数h将原来的第r行放在排列转换后次序中的第h®个位置上。

  因此，我们就可以不对行选择n个随机排列转换，取而代之的是随机选择n个哈希函数$h_1,h_2,...h_n$作用于行。在上述处理基础上，就可以根据每行在哈希之后的位置来构建签名矩阵。令SIG(i,c)为签名矩阵中第i个哈希函数在第c列上的元素。一开始，对于所有的i和c，将SIG(i,c)都初始化为$\infty$.然后，对r进行如下处理：

$h_1(r),h_2(r),...h_n(r)$

对每列c进行如下操作：

(a)如果c在第r行为0，则什么都不做

(b)否则，如果c在第r行为1，那么对于每个i=1,2,…,n,将SIG(i,c)置为原来的SIG(i,c)和$h_i(r)$中的较小值。

  使用上面的特征矩阵，在前面加上行号，在后面加上哈希函数对行号散列后的值形成下图，这里使用2个哈希函数 $h_1(x)=(x+1)\mod 5 $ ,$h_1(x)=(3x+1)\mathrm{m}\mathrm{o}\mathrm{d}5$

  签名计算流程为下图

  通过上面签名矩阵可以看出$Jac(S_1,S_4)=1$而真实的$Jac(S_1,S_4)=\frac{2}{3}$,这里签名的相似度只是一个真实相似度的估计值，本例中数据规模太小，不足以说明大规模数据下相似度的估计程度。

最小函数族总结

  这里给出一个完整的相似项发现算法:首先找出可能的候选对相似文档集合，然后基于该集合发现真正的相似文档。

  这里还是4000万文档，计算机单核计算能力$2\times 10^8$,采用20个band，每个band5行,每个文档取20个特征。总的计算量为：

生成minhash签名:$4\times 10^7\times 100\times 20$

哈希到相应的桶中:$4\times 10^7\times 20$

两两计算相似度:$4\times 10^7\times 20\times C$这里C为常数，假设为100

总的计算量:$4\times 10^7\times 4020$

单核用时: $800s$

  但是上面最小哈希函数族并不能满足要求，因为jaccard距离是没有权重的，而实际中往往是有特征权重的，接下来就讨论除最小函数族之外的的其它函数族，他们也能非常高效地产生候选对

局部敏感函数理论

   上面介绍了LSH技术是一个具体函数族(最小哈希函数族)上的应用例子，这些函数可以组合在一起(如上面提到的行条化技术)来更有效的区分低距离对和高距离对。

  这些函数族必须满足以下3个条件：

  (1) 它们必须更可能选择近距离对而不是远距离对作为候选对。

  (2) 函数之间必须在统计上相互独立。

  (3) 他们必须在以下两个方面具有很高的效率：

    (a) 它们必须能在很短的时间内识别候选对，改时间远小于扫描所有对所花费的时间。

    (b) 他们必须能更好的组合在一起来避免伪正例和伪反例，组合后所花费的时间也必须远小于对的数目。

  这里考虑一个判定函数，它判定两个候选项是否为候选对。很多情况下，函数f会对两个输入项求哈希值，最后的判断取决于两个哈希值是否相等。当$f(x,y)$判定x和y是一个候选对时，用$f(x)=f(y)$来表示。同样的用$f(x)\ne f(y)$来表示$f(x,y)$判定x，y不是候选对。这种形式的一系列函数集合构成了所谓的函数族。

  令$d_1<d_2$是定义在某个距离测度d下的两个距离值。如果一个函数族F中每一个函数f都满足如下条件，则称其为:$(d_1,d_2,p_1,p_2)$敏感的函数族：

  (1) 如果$d(x,y)\le d_1$,那么$f(x)=f(y)$的概率至少是$p_1$

  (2) 如果$d(x,y)\ge d_2$,那么$f(x)\ne f(y)$的概率至少是$p_2$

  下图给出了一个示意图，该图表示的是$(d_1,d_2,p_1,p_2)$敏感的函数族中的一个给定函数对两个输入项判断是否候选对的期望概率情况。我们可以使$d_1$和$d_2$尽量靠近。当然这种靠近通常也会使得$p_1$和$p_2$相互靠近。后面会提供一种方法，在固定$d_1$和$d_2$的情况下尽量分开$p_1$和$p_2$。

面向Jaccard距离的局部敏感函数族

  目前为止，我们暂时只有一种找到局部敏感函数族的方法，即采用最小哈希函数族并假设距离测度采用Jaccard距离。

  对任意$d_1$,$d_2$,$0\le d_1\le d_2\le 1$，最小哈希函数族是$(d_1,d_2,1-d_1,1-d_2)$敏感的。

  证明: $\because$ 如果x，y的jaccard距离$d(x,y)\le d_1$

$\therefore sim(x,y)=1-d(x,y)\ge 1-d_1$

$\because$x和y的jaccard相似度等于最小哈希函数对x及y哈希之后结果相等的概率

$\therefore P(f(x)=f(y))\ge 1-d_1$

同理证明(2)

局部敏感函数族的放大处理

  假设给定一个$(d_1,d_2,p_1,p_2)$敏感的函数族F.我们可以对F进行与构造得到新的函数族$F^{\prime }$。$F^{\prime }$的定义如下:$F^{\prime }$的每个成员函数由r个F成员函数组成，其中r是一个固定常数。若f在$F^{\prime }$中，而f为F的函数成员$f_1,f_2,...f_r$中一个，当且仅当所有i都有$f_i(x)=f_i(y)$时，才有$f(x)=f(y)$。

  由于$F^{\prime }$的成员函数都是从F的成员函数中独立选出的，因此可以断言$F^{\prime }$是一个$(d_1,d_2,(p_1{)}^r,(p_2{)}^r)$敏感的函数族。也就是说，对于任意p，如果F的一个成员函数判定(x,y)是候选对的概率为p,那么$F^{\prime }$的一个成员函数相同判定的概率为$p^r$。

  另外一种构造方式称为或构造，他可以将一个$(d_1,d_2,p_1,p_2)$敏感的函数族F转换为
一个$(d_1,d_2,1-(1-p_1{)}^r,1-(1-p_2{)}^r)$敏感的函数族$F^{\prime }$。也就是说当且仅当存在一个或者多个i使 $f_i(x)=f_i(y)$时，才有$f(x)=f(y)$

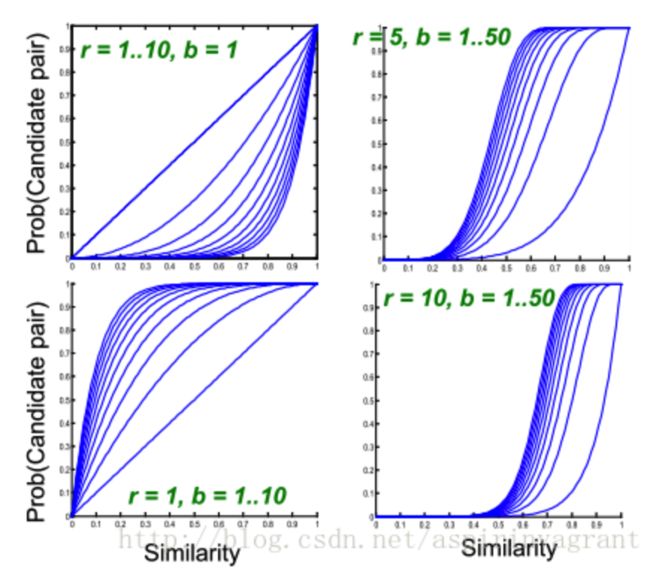
  我们注意到，与构造过程降低了所有的概率。但是如果能够谨慎选择F和r，就能使得小概率$p_2$非常接近于0，同时大概率$p_1$显著偏离0。类似的，或构造过程提升了所有的概率，但是通过谨慎选择F和r，能使得$p_1$接近于1而$p_2$有界远离1。通过任意次序串联与构造与或构造就可以使得$p_2$接近于0，同时$p_1$接近于1。

  不同r和b选择的情况下图像的样子如下

面向其它函数族的LSH

面向海明距离的LSH函数族

  假定一个d维向量空间，$h(x,y)$表示向量x和向量y之间的海明距离。选取向量的任意位置(如第i个位置),则定义函数$f_i(x)$为向量x的第i个位置上的分量，当且仅当x和y的第i个位置上的分量值相等时有$f_i(x)=f_i(y)$。对于随机选择的i，$f_i(x)=f_i(y)$的概率为$1-\frac{h(x,y)}{d}$，即向量x和向量y中相等分量所占的比例。

  上述情况和最小哈希遇到的情况几乎完全相同。因此，对任意$d_1<d_2$,由{ $f_1,f_2,...,f_n$}构成的函数族是$(d_1,d_2,1-\frac{d_1}{d},1-\frac{d_2}{d})$敏感的哈希函数族，它与最小哈希函数族仅有两点不同。

  (1) Jaccard距离的取值范围是0到1之间，而两个d维向量空间的海明距离的取值范围是0到d。因此，必须对海明距离除以d来转换成概率。

  (2) 本质上，最小哈希函数的形式可以有无限可能，而海明距离的函数族F的规模仅为d。

  因为海明距离的函数族F规模有限，所以其会限制S-曲线的陡峭程度。

  举例说明其计算过程：

  数据点集合P由以下6个点构成:A=(1,1) ,B=(2,1),C=(1,2),D=(2,2),E=(4,2),F=(4,3)

  可知坐标出现的最大值是4，则d=4,维度为2，则n=2，显然dC=8，我们进行8位海明编码

v(A) = 10001000

v(B) = 11001000

v© = 10001100

v(D) = 11001100

v(E) = 11111100

v(F) = 11111110

  若采用d=2 , r= 3生成哈希函数

  G由$g_1$,$g_2$,$g_3$构成，每个g由它对应的$h_1$,$h_2$构成，假设有如下结果。

$g_1$分别抽取2,4位。

$g_2$分别抽取1,6位。

$g_3$分别抽取3,8位。

  哈希表的分布如下图所示

  若此时我们查询点q=(4,4),可以计算出$g_1=[1,1{]}^T$,$g_2=[1,1{]}^T$,$g_3=[1,1{]}^T$。则分别取出表1，2，3的11，11，11号哈希桶的数据点与q比较。依次是C，D，E，F。算出距离q最近的点为F。原始搜索空间为6个点，现在搜索空间为4个点。

随机超平面和余弦距离

  两个向量的余弦距离是他们的夹角，夹角越小，成为候选对的概率越大。接下来讨论这个夹角和夹角相关的概率如何确定。

  答案就是通过一个哈希函数对这两个向量进行哈希，而这个哈希函数实际上只是一个随机的向量与这两个向量的内积，如果好多个这样的随机向量与他们的内积是同号的，则说明这两个向量的夹角很小，相似性大，否则相似性小。

  如下图，紫色虚线能将x和y哈希到同一位置，黄色的不能。

  对于任意的向量x和y，x和y之间的距离为x和y之间的夹角$\theta$.哈希函数为随机寻找一个向量v，如果 $x\times v$和 $y\times v$同号，则说明f(x) = f(y)，很明显，其概率为$1-\frac{\theta }{180}$。所以F具备$(d_1,d_2,1-\frac{d_1}{180},1-\frac{d_2}{180})$敏感性。

  随机向量v可以只由1和-1组成，因为夹角和向量的模无关，而只选择1或者-1方便计算。

  举例说明其计算过程：

  给定一个四维的向量空间，选出3个随机向量$v_1=[+1,-1,+1,+1]$,$v_2=[-1,+1,-1,+1]$,$v_3=[+1,+1,-1,-1]$。那么对于向量x=[3,4,5,6]。计算过程如下:$v_1\times x=3-4+5+6=10>0$因此其梗概的第一个元素为+1。类似的,$v_2\times x=3$且$v_3\times x=-4$。因此梗概的第二个元素和第三个元素分别是+1和-1.

  考虑向量y=[4,3,2,1],可以采用上述类似的方法计算其梗概为$[+1,-1,+1]$。由于x和y的梗概中相同元素的比例为$\frac{1}{3}$，因此可以估计这两个向量间夹角为$1-\frac{\theta }{180}=\frac{1}{3}$,其中$\theta =120$

  但是上述结论却大错特错。我们可以计算这两个向量的的夹角为$\theta =\frac{6\times 1+5\times 2+4\times 3+3\times 4}{\sqrt{6^2+5^2+4^2+3^2}\times \sqrt{1^2+2^2+3^2+4^2}}=0.7875$大约为38度左右。但是上面结果错误是法向量采样问题，如果选择所有的16个不同的四维+1,-1向量就会发现，其中只有4个向量与x的内积和与y的内积符号相反。因此，如果选择16个向量来构成梗概的话，那么最后的夹角估计结果为$1-\frac{\theta }{180}=\frac{12}{16}$ 为45度。

面向欧式距离的LSH函数族(E2LSH)

  欧式空间中，LSH的hash算法的思路是将n维向量随机射到一个向量，使用向量点乘，由于投射向量不是单位向量，所以严格意义上不能称之为投影。投射hash算法如下:

$h(v)=\lfloor \frac{a\bullet v+b}{w}\rfloor$

  其中$b(\in [0,w])$是随机量，$a(\in R^n,a_i\sim N(0,1))$，是被投射的向量。投射完后，需要设置一个固定长度为w的参数，将向量严格的划分为不同的单位，投射到相同单位的向量就认为比较近。所以，w的设置十分重要，如果设置太大，比较远的对象也设hash到一个单位里，无法做到过滤的效果；如果太小，即使很近的对象也到不了一个桶里面，导致找不到相邻的对象。

碰撞概率分析

  设向量$p,q\in R^n$，并且$u=\Vert p-q{\Vert }_2$，p与q投射到任意向量
a
的概率如下，

$p(u,w)=Pr(h(p)=h(q))=2{\int }_0^w\frac{1}{u}f(\frac{t}{u})(1-\frac{t}{w})dt$

  上面概率公式很突然，先别慌是怎么过来的，后面慢慢道来，我们先直奔主题:$p(u,w)$
的解析解。观察w,u与概率的关系，控制碰撞概率。$f(x)$
是稳定分布的概率密度函数，该分布只有在欧式距离和曼哈顿距离才有解析解，否则没有。好在我们关心的是欧式空间，所以可以得到解析解。欧式空间中，$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$是标准正在分布的概率密度函数。完整推导如下，

$\begin{array}{ll}p(u)& =2({\int }_0^w\frac{1}{u}f(\frac{t}{u})dt-{\int }_0^w\frac{1}{u}f(\frac{t}{u})\frac{t}{w}dt)\\ & =2({\int }_0^{w}f(\frac{t}{u})d\frac{t}{u}-{\int }_0^w\frac{1}{u\sqrt{2\pi }}{e}^{-\frac{t^2}{2u^2}}\frac{t}{w}dt)\\ & =2({\int }_0^{\frac{w}{u}}f(x)dx-\frac{-u}{\sqrt{2\pi }w}{\int }_0^w{e}^{-\frac{t^2}{2u^2}}d(-\frac{t^2}{2u^2}))\\ & =2(\frac{1}{2}-F(-\frac{w}{u})+\frac{u}{\sqrt{2\pi }w}{e}^{-\frac{t^2}{2u^2}}{|}_0^w)\\ & =2(\frac{1}{2}-F(-\frac{w}{u})+\frac{u}{\sqrt{2\pi }w}(e^{-\frac{w^2}{2u^2}}-1))\end{array}$

  令$c=\frac{u}{w}$

$g(c)=1-2F(-\frac{1}{c})+\sqrt{\frac{2}{\pi }}c(e^{-\frac{1}{2c^2}}-1)$

  上面推导的结果只与c有关，无需考虑数据真实的单位.画出上面函数的图像为下图：

  根据曲线，上述函数是关于c的减函数，也就是比例越大，聚到一起的概率越低，理论与直觉一致。可以通过设定u，然后通过曲线设置一个概率，得到对应w。通过计算导数，也可以很容易发现其值恒为复数，如下：

$\begin{array}{ll}p(u)& =2({\int }_0^w\frac{1}{u}f(\frac{t}{u})dt-{\int }_0^w\frac{1}{u}f(\frac{t}{u})\frac{t}{w}dt)\\ & =2({\int }_0^{w}f(\frac{t}{u})d\frac{t}{u}-{\int }_0^w\frac{1}{u\sqrt{2\pi }}{e}^{-\frac{t^2}{2u^2}}\frac{t}{w}dt)\\ & =2({\int }_0^{\frac{w}{u}}f(x)dx-\frac{-u}{\sqrt{2\pi }w}{\int }_0^w{e}^{-\frac{t^2}{2u^2}}d(-\frac{t^2}{2u^2}))\\ & =2(\frac{1}{2}-F(-\frac{w}{u})+\frac{u}{\sqrt{2\pi }w}{e}^{-\frac{t^2}{2u^2}}{|}_0^w)\\ & =2(\frac{1}{2}-F(-\frac{w}{u})+\frac{u}{\sqrt{2\pi }w}(e^{-\frac{w^2}{2u^2}}-1))\end{array}$

  导数严格小于0，证实了上述曲线确实严格下降。

碰撞概率推导过程

  本节详细介绍如何得到上面的概率公式。假设$t=a\bullet v_1-a\bullet v_2$是向量$v_1$，$v_2$投影到a上距离，必须$|t|\le w$才有$Pr(h(v_1)=h(v_2))>0$所以当$v_1$，$v_2$投影距离为t时，且t>0时碰撞的概率为$1-\frac{t}{w}$。但是t的概率是什么呢？t与投影向量有关，同时与向量$v_1$，$v_2$也有关。

  这里需要利用稳定分布。这是一类分布，如果任意分布D是稳定分布，那么任意n个D的独立同分布随机变量$X_1,X_2,\cdots ,X_n$,在任意n个实数$v_1,v_2,\cdots ,v_n$,有${\sum }_{i=1}^n(v_i{X}_i)$与$(\sum |v_i{|}^s{)}^{\frac{1}{s}}X$(X也是D的一个随机变量)有相同的分布。可以利用这个分布计算t的概率分布。

  对于随机变量$t=a(v_1-v_2)=\sum a_i(v_{1i}-v_{2i})$,只要$a_i$的概率分布固为D，t的分布与$(\sum |v_{1i}-v_{2i}{|}^s{)}^{\frac{1}{s}}a$一致。且当$s=2$时，分布D是标准正太分布。(只有S等于2或1，D的分布才有解析解，否则没有)。在s=2的情况下，设a的概率密度函数为$f_A(a)$,且$u=(\sum |v_{1i}-v_{2i}{|}^2{)}^{\frac{1}{2}}$,那么$f_T(t)=\frac{1}{u}{f}_A(\frac{t}{u})$有了t的概率密度函数，对于任意t的概率为$\frac{1}{u}{f}_X(\frac{t}{u})dt$结合概率积分，得到概率最后的碰撞概率公式:$p(w,u)=2{\int }_0^w\frac{1}{u}{f}_X(\frac{t}{u})(1-\frac{t}{w})dt$，当$t\in [-w,0]$时，概率与$[0,w]$一致，所以乘以2；其他范围概率均为0。

欧式空间中的$(r_1,r_2,p_1,p_2)-sensitive$

  上面讨论的投射方法和碰撞概率函数，就是分别对应上面定义的h和P。尤其是碰撞函数，可以根据给出的$r_1$和$r_2$情况估算$p_1$和$p_2$，并且计算最优的w的范围。首先，回顾一下碰撞函数:

$P(h(v)=h(q))=g(c)=1-2F(-\frac{1}{c})+\sqrt{\frac{2}{\pi }}c(e^{-\frac{1}{2c^2}}-1)$

  其中$c=\frac{u}{w}$,假设$r_1=5,r_2=50,p_1=0.95,p_2=0.1$。根据碰撞概率的解析公式，可以得到$p_1$,$p_2$对应的数值解。即$c_1=g^{-1}(p_1),c_2=g^{-1}(p_2)$。由于概率公式是减函数，所以

$\begin{array}{ll}g(c_1)\ge p_{1}andg(c_2)\le p_2& \Rightarrow c_1\le g^{-1}(p_1)and{c}_2\ge g^{-1}(p_2)\\ & \Rightarrow \frac{r_1}{w}\le g^{-1}(p_1)and\frac{r_2}{w}\ge g^{-1}(p_2)\\ & \Rightarrow \frac{r_1}{g^{-1}(p_1)}\le w\le \frac{r_2}{g^{-1}(p_2)}\\ & \Rightarrow \frac{5}{g^{-1}(0.95)}\le w\le \frac{50}{g^{-1}(0.1)}\end{array}$

  $p_1$,$p_2$与$r_1$,$r_2$可以根据应用精度和数据范围，人工估算。通过碰撞公式，完美的解决了w的取值问题，非常具有指导意义。但是，上述不等式不是永远成立的，部分$p_1$,$p_2$与$r_1$,$r_2$的组合可能导致不等式下界大于上界。

强化LSH函数

  强化LSH函数，可以不改变LSH算法的情况下，通过增加运算量，提高精度。假设有一个$(r_1,r_2,p_1,p_2)-sensitive$函数族$F$，可以通过逻辑与的方法构造一个新的函数族$F^{\prime }$.

  假设$f\in F^{\prime }$并且$f_i\in F,i=1,2,\cdots r$令$f(x)=f(y)$为$f_i(x)=f_i(y),i=1,2,\cdots ,r$，此时$F^{\prime }$是$(r_1,r_2,p_1^r,p_2^r)-sensitive$。如果$p_2$较小$p_1$较大，可以通过此操作将其进一步的缩小，同时有不会将$p_1$变得太小。

  同理，可以使用逻辑或的方法，将其变成一个$(r_1,r_2,1-(1-p_1{)}^r,1-(1-p_2{)}^r)-sensitive$。其效果与逻辑和相反，它将概率均变大。

  常用的方法是将逻辑与嵌套到逻辑或中使用，得到$(r_1,r_2,1-(1-p_1^k{)}^L,1-(1-p_2^k{)}^L)-sensitive$函数族（先使用逻辑与，再使用逻辑和也可）。这种组合的意义是去掉那些碰巧hash到一起的情况，如果真的很近，在L组计算中，总有一组k个hash均相等。k和L需要设置合理，L如果设置太大，计算开销会增加。给定k，增强的概率比原来要好，即${\rho }_1\le 1-(1-p_1^k{)}^L,{\rho }_2\ge 1-(1-p_2^k{)}^L$，可以得到L的范围:

$\frac{\ln (1-{\rho }_1)}{\ln (1-p_1^k)}\le L\le \frac{\ln (1-{\rho }_2)}{\ln (1-p_2^k)}$

  L取范围内最小的整数，节省空间。桶里，上面不等式不保证永远成立，条件太苛刻时需要调整。

E2LSH的工作流程

  前面理论讲了很多，现在介绍LSH的工作流程。大体步骤分为两步：1）创建hash表；2）对象聚集。

1. 创建hash表

  如果不使用增强hash函数，理论上只需要一个hash表即可。但是从实际应用来看，一个hash表要不够精确。最佳实践是创建$k\times L$
个hash表，每一个表的hash函数均是使用标准正太分布随机生成投影向量和均匀分布生成随机偏移量。每k个hash表为一组，称为一个“桶”，共L个桶。生成过程如下：

  由于随机的原因，可能有些比较近的对象在一个桶内会hash到不同的位置，但是我们给了L个桶，即L此碰撞机会。如果他们真的相似，总有可能在其他桶里面hash到同一个位置（该桶内所有k个hash值均相等）。

2. 对象聚集

  hash表创建完毕后，只是给每个对象一堆$k\times l$标记，实际上相似的对象并没有在一起。需要将这些标记，每k个合并为一个id，然后按照id聚合。生成id使用两段hash函数$h_1$,$h_2$计算方法如下

$\begin{array}{l}{h}_1=a\bullet v\mathrm{m}\mathrm{o}\mathrm{d}p\mathrm{m}\mathrm{o}\mathrm{d}n\\ h_2=b\bullet v\mathrm{m}\mathrm{o}\mathrm{d}p\end{array}$

  其中$a,b\in R^k$,且$a_i,b_i$是随机整数.p
是一个很大的质素，通常$p=2^{32}-5$；n是源数据条数。如果只使用1个hash函数，n较大时，冲撞的概率不可以忽略；但是如果使用两个hash函数，冲撞的概率基本可以忽略不计。整个过程示意图如下：

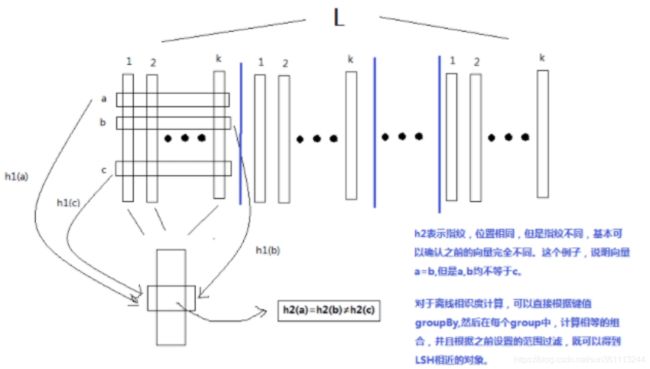
  合并后，同一个key下的所有对象就是比较近的对下。然后根据事先设定的相似度阀值，得到阀值以内的相似对象。