元胞自动机之生命游戏的MatLab实现(考虑边界问题)
文章目录
-
- 一、元胞自动机CA
- 二、生命游戏
- 三、生命游戏的MatLab实现
- 四、实现效果及其分析
一、元胞自动机CA
元胞自动机(cellular automata,CA) 是一种时间、空间、状态都离散,空间相互作用和时间因果关系为局部的网格动力学模型,具有模拟复杂系统时空演化过程的能力。[参考百度百科]
其中,元胞自动机又称为细胞自动机,而生命游戏(Game of Life)又是一种十分典型的CA。
以下是我做的笔记,CA一共有四个要点:

二、生命游戏
The Game of Life (生命游戏) ,是由英国数学家 John Horton Conway于1970年提出的。作为元胞自动机系统,生命游戏是一个零玩家游戏,用户确定初始状态与演变的规则后,无须其他操作,便可模拟得到形态的演变过程。
元胞自动机的基本思想可以追溯到上世纪Von Neumann在“Theory of Self-Reproducing Automata”提出的“机器繁殖”一概念:由一群细胞构成的小机器根据一些简单规则和初始图形进行演化的动力系统,机器可以不断自我进化和延续。[参考链接]
三、生命游戏的MatLab实现
我认为网上大多数代码都没有考虑到边界问题,所以我进行了一定的改进。
游戏规则在注释有详细解释,一共有三条。
下面这个表格帮助大家理解:(想象一下左下角是原点坐标)
| (i+1,j-1) | (i+1,j) | (i+1,j+1) |
| (i,j-1) | (i,j) | (i,j+1) |
| (i-1,j-1) | (i-1,j) | (i-1,j+1) |
下面是代码实现
%元胞自动机之生命游戏
%规则:假设元胞只有生和死两种状态
%1. 如果一个活细胞周围(包括对角相邻)有2或3个细胞为生,则该细胞保持为生;
%2. 如果一个死细胞周围有3个细胞为生,则该细胞转为生;
%3. 在其它情况下,死细胞保持死,活细胞转为死。
clc;
clear;
%定义元胞空间的大小为100,也即是100个元胞
x = 20;
y = 20;
%定义迭代次数
epoch = 100;
%初始化网格点
net = rand(x,y);
game = zeros(x,y);
for i = 1:x
for j = 1:y
if net(i,j)<= 0.3
% 按照(i-1,j)->(i,j)->(i,j-1)->(i-1,j-1)进行勾勒图形
fx = [i-1,i,i,i-1];
fy = [j,j,j-1,j-1];
fill(fx,fy,'g')
%表示元胞状态为生
game(i,j)=1;
hold on
end
end
end
pause(0.1)
for k = 1:epoch
temp = zeros(x,y);
fx=[0,x,x,0];
fy=[0,0,y,y];
fill(fx,fy,'w');
hold on;
for i = 1:x
for j = 1:y
if i~=1 && i~= x && j~=1 && j~=y
%在四个角邻居只有三个,在边界邻居只有五个
a = game(i-1,j-1)+game(i,j-1)+game(i+1,j-1)+game(i-1,j)+game(i+1,j)+game(i-1,j+1)+game(i,j+1)+game(i+1,j+1);
if game(i,j) == 1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a== 3
temp(i,j) = 1;
end
end
elseif i==1
if j==1
a = game(i,j+1)+game(i+1,j)+game(i+1,j+1);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
elseif j==y
a = game(i,j-1)+game(i+1,j-1)+game(i+1,j);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
else
a = game(i,j-1)+game(i+1,j-1)+game(i+1,j)+game(i,j+1)+game(i+1,j+1);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
end
elseif i == x
if j==1
a = game(i-1,j)+game(i-1,j+1)+game(i,j+1);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
elseif j==y
a = game(i-1,j-1)+game(i-1,j)+game(i,j-1);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
else
a = game(i-1,j-1)+game(i,j-1)+game(i-1,j)+game(i-1,j+1)+game(i,j+1);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
end
elseif j == 1
a = game(i-1,j)+game(i+1,j)+game(i-1,j+1)+game(i,j+1)+game(i+1,j+1);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
elseif j == y
a = game(i-1,j-1)+game(i,j-1)+game(i+1,j-1)+game(i-1,j)+game(i+1,j);
if game(i,j)==1
if a == 3 || a ==2
temp(i,j) = 1;
end
else
if a == 3
temp(i,j) = 1;
end
end
end
end
end
if game == temp
disp(strcat('在第',num2str(k),'轮元胞自动机达到稳态'))
for i=1:x
for j=1:y
if temp(i,j)==1
fx=[i-1,i-1,i,i];
fy=[j-1,j,j,j-1];
fill(fx,fy,'g');
hold on;
end
end
end
break;
end
game = temp;
for i=1:x
for j=1:y
if game(i,j)==1
fx=[i-1,i-1,i,i];
fy=[j-1,j,j,j-1];
fill(fx,fy,'g');
hold on;
end
end
end
pause(0.1)
end
四、实现效果及其分析
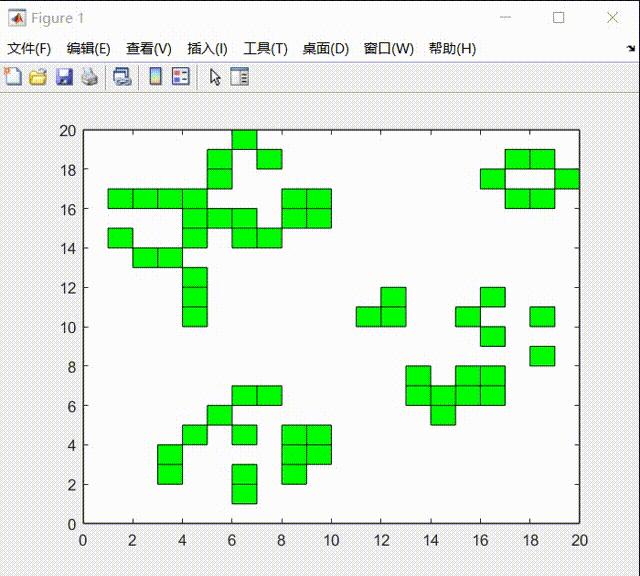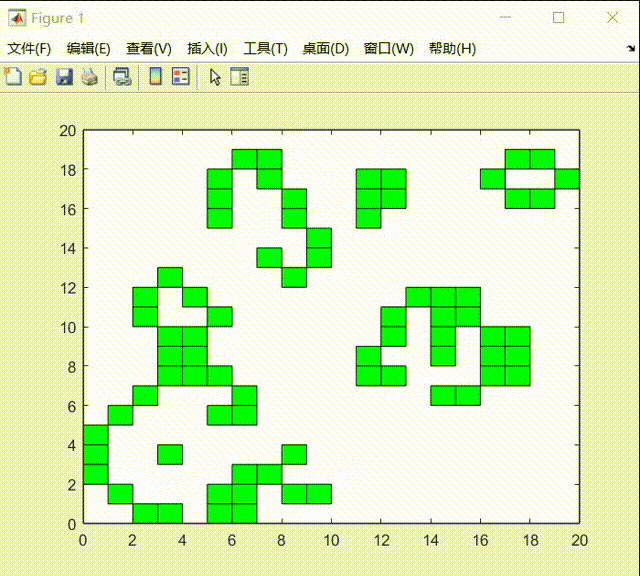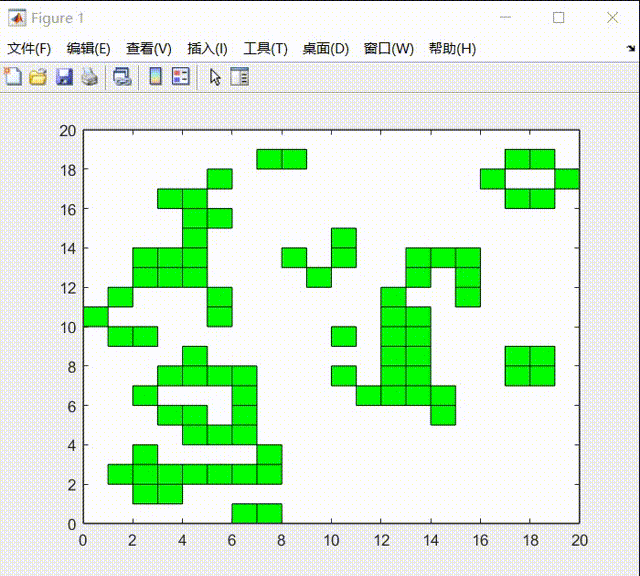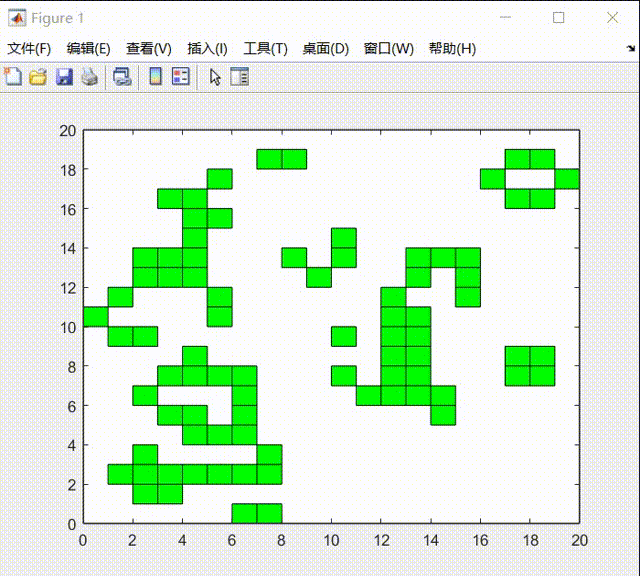
其中初始状态我用均匀分布初始化矩形框,在20*20的区域内,在实验过程中进行如下演示:
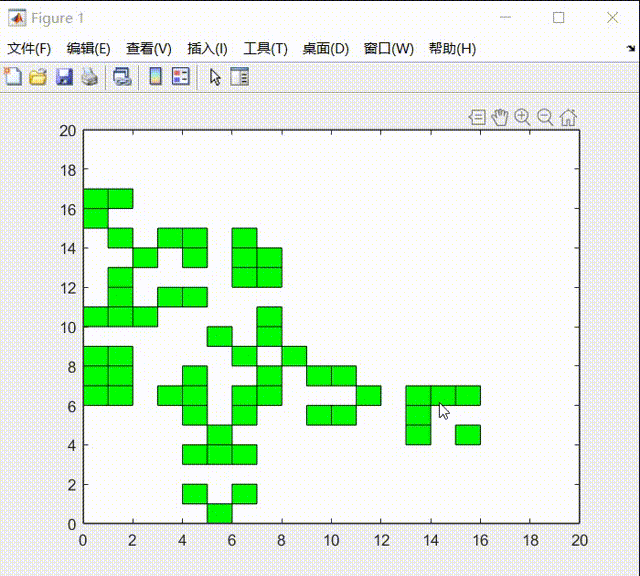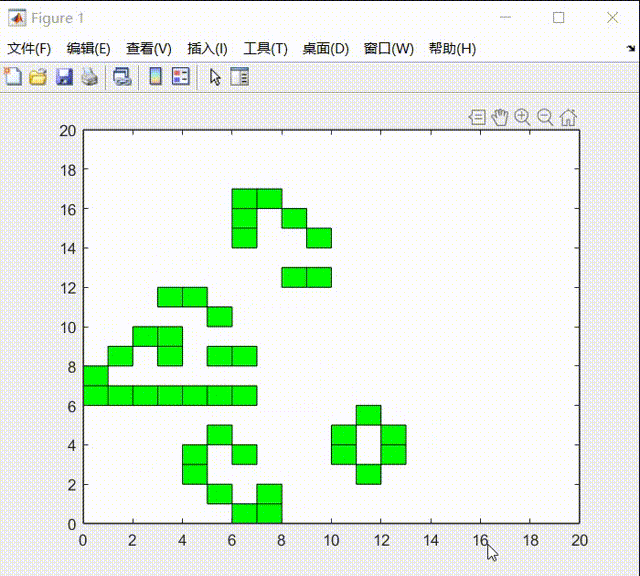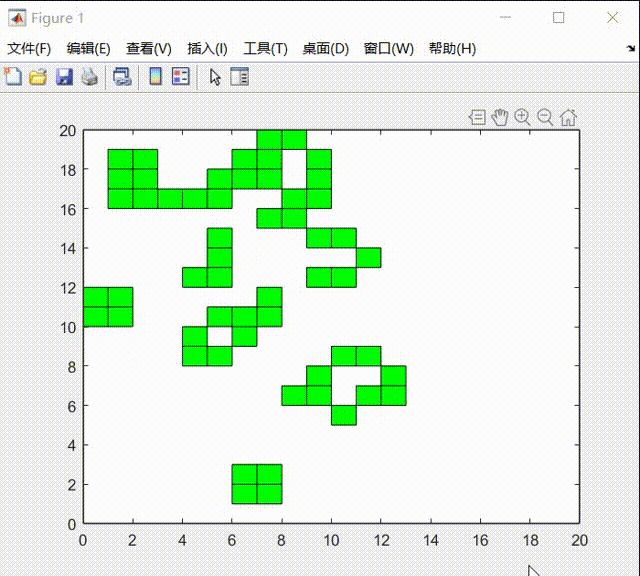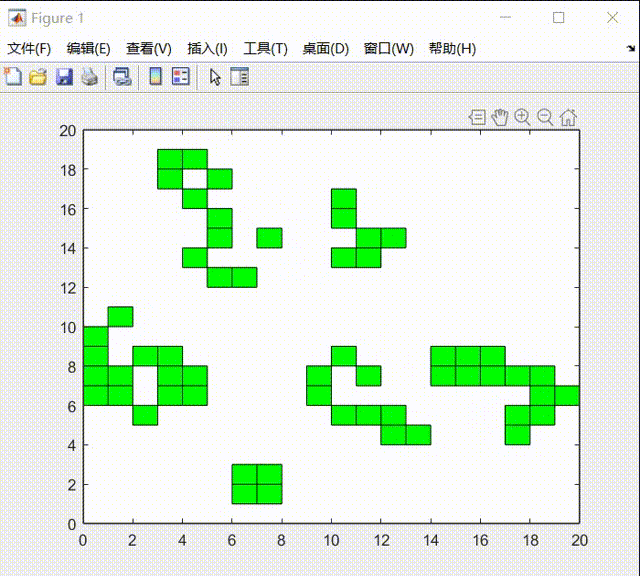
在实验的最后中,我发现生命游戏的元胞自动机系统在最后会达到稳态:
我认为一共分为两类:
1)一类是周期类型的运动:
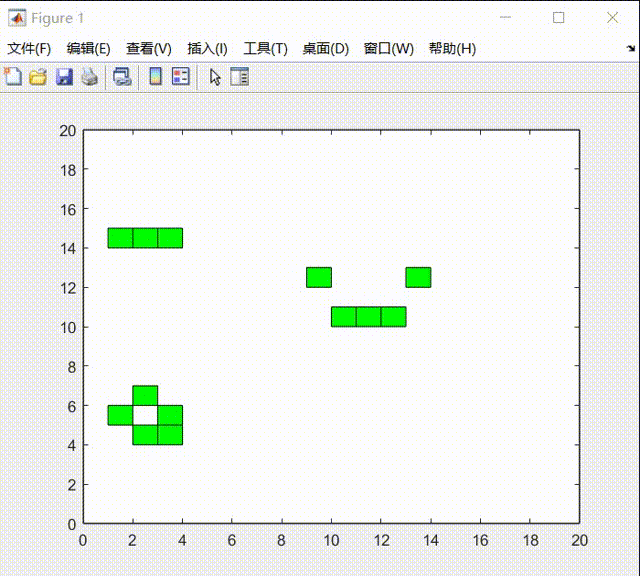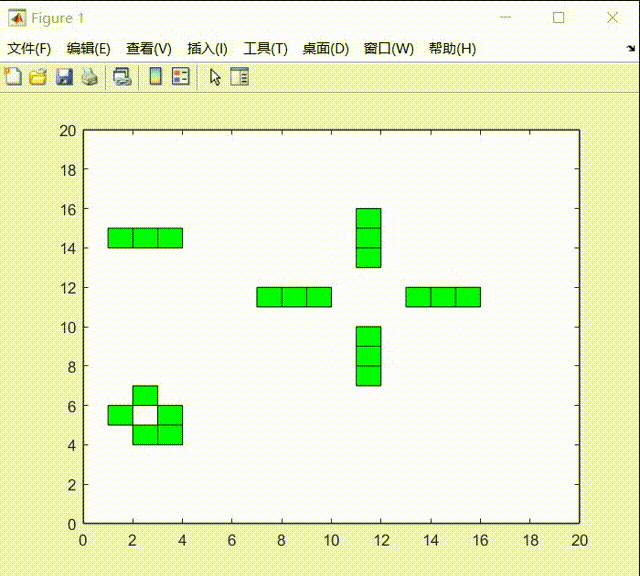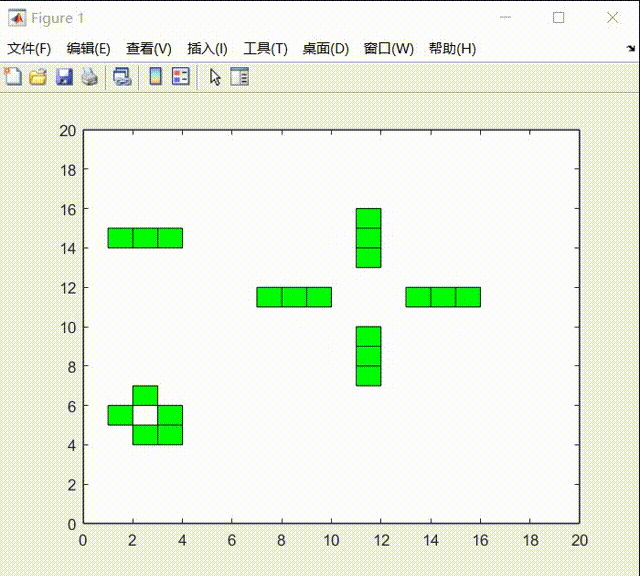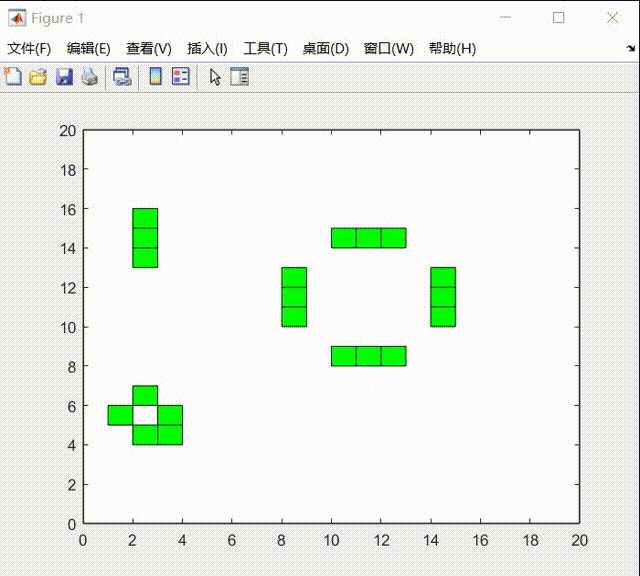
2)一类是达到稳态后时静止:
ps: 转载请注明出处!如有缺漏请指正,祝大家学有所成!