指数分布和卡方分布的期望方差关系_泊松分布、指数分布、gamma分布
概率分布相关内容: 1 概率密度 2 期望与协方差 3 一元高斯分布 [1] 4 多元高斯分布 [2] 5 高斯混合简介 6 gamma函数、digamma函数、beta函数 7 伯努利分布、beta分布、Dirichlet分布
本文主要包含以下内容:
1 泊松分布
2 泊松分布近似二项分布
3 指数分布
4 gamma分布
1 泊松分布
泊松分布(poisson distribution),以Simeon Denis Poisson (1781-1840) 的名字命名。泊松分布是一种离散分布。它描述了在一个单位时间或空间内很少发生的随机事件。
它与二项分布的不同之处在于后者计算成功或失败的次数,而前者计算单位时间或空间内成功或失败的平均次数。
泊松分布只有一个参数,用表示。参数必须大于0。其形式如下:
在进行下一步之前,大家可以看一下e的简介和e的一般定义。里面有一个重要的定义,即以周期为1的增长率满足:
式其中表示单位时间内的平均增长率或单位时间内事件出现的平均次数,即上面的;表示事件的次数。
泊松分布是归一化的:
泊松分布的均值和方差分别为:
式式式4和式5的证明:
均值:
方差(结合均值):
2 泊松分布近似二项分布
泊松分布是二项分布在下列假设下的极限情况:
- 试验次数应无限大,即
- 每次试验成功的概率都是无限小
- ,是一个常数
从次抛掷一枚非均匀硬币的概率分布开始。假设为投掷一次得到正面的概率,远小于1 ()。因此,在抛硬币的长序列中,出现正面是罕见(rare)的事件。在次抛掷中观察到个正面的概率是:
这里使用两个近似:
当时:
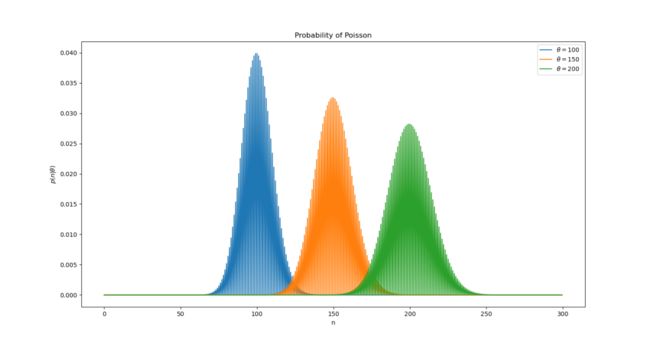
绘制不同的poisson分布图:
from scipy.stats import poissonimport matplotlib.pyplot as pltimport numpy as np
n = np.arange(0,300,0.5)
theta = [100,150,200]
plt.figure(figsize=(15,8))for a in theta:
plt.plot(n,poisson.pmf(n,a),label=r'$\theta=%s$'%a)
plt.title('Probability of Poisson')
plt.xlabel('n')
plt.ylabel(r'$p(n|\theta)$')
plt.legend()
3 指数分布
连续随机变量如果具有下面的概率密度函数,则称为具有指数分布:
其中称为分布的速率(rate)。
在连续时间的随机过程的研究中,通常用指数分布来模拟(预测)过程中发生某件事(成功、失败等)之前的等待时间并采用部分积分法计算指数分布的均值和方差:
证明式10和式11:
均值:
所以我们可以看到,随着逐渐变大,我们等待的过程会发生得更快,因此我们把看作是速率。
方差:
指数分布为什么是式9的形式?
指数分布的定义是泊松过程中事件之间时间的概率分布。试想一下,直到事件发生的时间量意味着在等待期间,没有一个事件发生。
换句话说,这就是,即:
关于泊松概率分布需要记住的一点是,泊松事件发生的时间周期只是一个单位时间。
如果想建立时间段内什么都没有发生的概率分布的模型,而不只是在一个单位时间内,则:
泊松分布假设事件的发生是相互独立的。因此,我们可以通过将单位时间内的乘以次来计算单位时间内零成功的概率。
PDF是CDF的导数。因为我们已经有了指数函数的CDF,即,我们可以通过微分得到它的PDF。
指数分布的属性:
- 无记忆性(Memoryless Property):
泊松分布与指数分布间的联系:如果单位时间内的事件数服从泊松分布,则事件之间的时间量服从指数分布。假设事件之间的时间不受前一事件之间时间的影响(即事件独立),则单位时间内的事件数服从于速率的泊松分布。
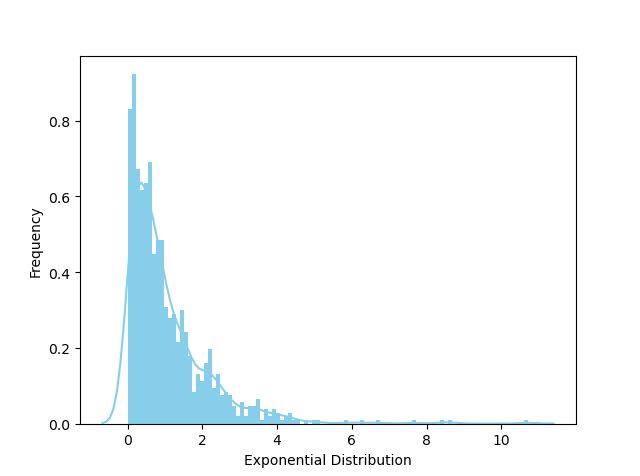
绘制指数分布图:
from scipy.stats import exponimport seaborn as snsimport numpy as np# 生成随机数
data = expon.rvs(scale=1,loc=0,size=1000)
ax=sns.distplot(data,kde=True,bins=100,color='skyblue',
hist_kws={
'linewidth':15,'alpha':1})
ax.set(xlabel='Exponential Distribution',ylabel='Frequency')
4 gamma分布
在该文中介绍了gamma的标准分布:
其中。
但在概率论和统计中,伽马分布是一个连续概率分布的双参数族。指数分布、Erlang分布和卡方分布是伽玛分布的特殊情况。有三种常用的参数化方法:
- 形状参数,尺度参数
- 形状参数,反尺度参数,又叫速率参数
就像我们处理指数分布一样,我们从泊松分布中得到它。设为随机变量,表示等待时间。其累积分布函数为:
注意是在区间内小于个事件的概率。在均值为的泊松过程中的概率是:
为了求概率分布函数,我们对求导。但在此之前,我们可以简化一下将求和展开为两项:
下面求导:
所以,两参数的gamma分布为:
或
当,式15是指数分布;当是一个正整数,则为Erlang分布;当时,得到标准分布式12。
伽玛分布的一种解释是,它是泊松过程中等待第事件或变化的时间的理论分布。指数分布,它是直到泊松过程中第一个事件或变化的时间分布。伽马分布模拟了泊松过程中到第2、第3、第4、第38等时刻的事件或变化。
两参数的gamma分布的均值为(以式15为例):
证明式17和式18:
令,则。
均值:
上式利用了gamma函数的积分公式。
方差:
绘制gamma分布图:
import numpy as npfrom scipy.stats import gammaimport matplotlib.pyplot as plt
x=[1,2,3,3,3]
lambda_=[0.5,0.5,0.5,1,2]
color = ['b','r','g','y','m']
t = np.linspace(1E-6,10,1000)
fig,ax=plt.subplots(figsize=(8,6))for k,l,c in zip(x,lambda_,color):
dist = gamma(k,0,l)
plt.plot(t, dist.pdf(t), c=c, label=r'$x=%.1f,\ \lambda=%.1f$' % (k, l))
plt.xlim(0, 10)
plt.ylim(0, 2)
plt.xlabel('$t$')
plt.ylabel(r'$p(t|x,\lambda)$')
plt.title('Gamma Distribution')
plt.legend(loc=0)
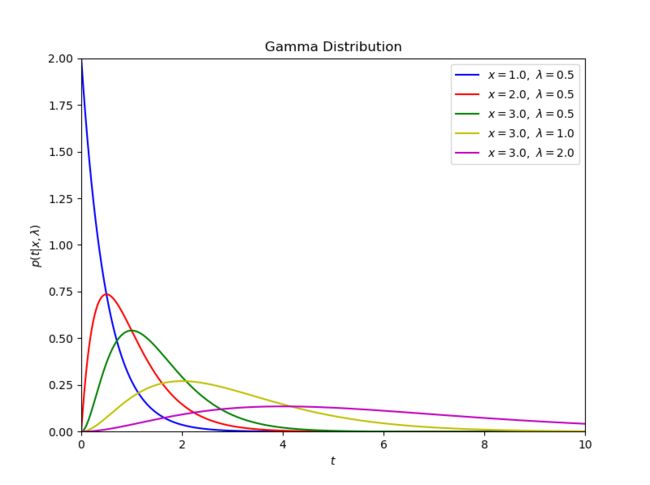
gamma函数通常是右倾斜的,其峰值通常会出现在PDF图的左侧。当形状参数小于1时,伽马分布将在PDF图上渐近于y轴,如上图所示。当形状参数超过1时,图会显得更加分散或延伸,整体歪斜减小;尺度参数决定了曲线有多陡,其越小越陡,即速率参数越大越陡。
参考资料
[1]一元高斯分布: https://blog.csdn.net/mengjizhiyou/article/details/103919140
[2]多元高斯分布: https://blog.csdn.net/mengjizhiyou/article/details/103933591

