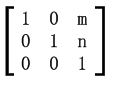OpenCV-Python图像处理:仿射变换详解及案例
仿射变换博文传送门(带星号的为付费专栏文章):
- *图像仿射变换原理1:齐次坐标来龙去脉详解
- *图像仿射变换原理2:矩阵变换、线性变换和图像线性变换矩阵
- *图像仿射变换原理3:仿射变换类型及变换矩阵详解
- *图像仿射变换原理4:组合变换及对应变换矩阵
- *图像仿射变换原理5:组合变换矩阵的OpenCV-Python实现
- OpenCV-Python图像处理:仿射变换详解及案例
- OpenCV-Python仿射变换开发中遇到的坑
- openCV仿射变换:getAffineTransform的案例
- 为什么称图像旋转、错切、缩放变换是线性变换?
- 图像仿射变换:绕点旋转和指定直线依赖轴shear错切变换矩阵
- 图像仿射变换shear怎么翻译?剪切、错切、推移哪个译词好?
- 仿射变换原理和其OpenCV-Python实现知识汇总
一、概述
图像的几何变换包括透视变换和仿射变换,透视变换又称为投影变换、投射变换、投影映射,透视变换是将图片投影到一个新的视平面,它是二维(x,y)到三维(X,Y,Z)、再到另一个二维(x’,y’)空间的映射。仿射变换可以认为是投射变换的一种特殊情况,是透视变换的子集,仿射变换是从二维空间到自身的映射。
仿射变换包括平移(translation)、旋转(rotation)、缩放(scaling)、错切(shear )四种类型:
- 平移和旋转两者的组合不改变图像的大小和形状,只有图像的位置(平移变换)和朝向(旋转变换)发生改变,称之为欧式变换(Euclidean transformation)或刚体变换(rigid transformation),刚性变换是最一般的变换
- 缩放又分为等比例缩放(uniform scaling)和非等比例缩放(non-uniform scaling),如果缩放系数为负数,则会叠加翻转(reflection,又翻译为反射、镜像),因此翻转可以看成是特殊的缩放
- 欧式变换和等比例缩放保持了图像外观没有变形,因此二者的组合称为相似变换(similarity transformation)
- 错切是保持图形上各点的某一坐标值不变,而另一坐标值关于该保持不变坐标值进行线性变换。坐标不变的轴称为依赖轴,其余坐标轴称为方向轴。错切分为水平错切和垂直错切。
二、基本仿射变换矩阵
在《https://blog.csdn.net/LaoYuanPython/article/details/113788380 图像仿射变换原理3:仿射变换类型及变换矩阵详解》中介绍了包括平移(translation)、旋转(rotation)、缩放(scaling)、错切(shear )四种类型仿射变换的变换矩阵。
-
上面介绍的仿射矩阵实际上并不是标准称呼上的仿射矩阵,而是一种用于两个平面间进行透视变换的
3*3单应性矩阵,真正的仿射矩阵是2*3的矩阵,比单应性矩阵少一行,OpenCV中warpAffine函数使用的矩阵就是2*3的矩阵。
三、仿射变换相关函数介绍
3.1、warpAffine函数
在OpenCV中,仿射变换可以通过函数warpAffine来支持,当然部分单独的函数也可以进行某个特定的变换,如缩放和旋转就有单独的变换函数。
3.1.1、调用语法
warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)
3.1.2、语法说明
- src:输入图像矩阵
- M:2*3的仿射变换矩阵,可以自己构建,也可以通过getAffineTransform、getRotationMatrix2D等函数获取
- dsize:结果图像大小,为宽和高的二元组
- dst:输出结果图像,可以省略,结果图像会作为函数处理结果输出
- flags:可选参数,插值方法的组合(int 类型),默认值 INTER_LINEAR,具体取值及含义请参考《https://blog.csdn.net/LaoYuanPython/article/details/111771138 OpenCV-Python图像处理:插值方法及使用resize函数进行图像缩放》的介绍
- borderMode:可选参数,边界像素模式(int 类型),默认值 BORDER_CONSTANT,具体取值及含义请参考《https://blog.csdn.net/LaoYuanPython/article/details/109441709 OpenCV-Python图像处理:腐蚀和膨胀原理及erode、dilate函数介绍》的介绍
- borderValue:可选参数,边界填充值,当borderMode为cv2.BORDER_CONSTANT时使用,默认值为None。另外当borderMode取值为cv2.BORDER_TRANSPARENT时,目标图像中与源图像中的离群值相对应的像素不被函数修改(关于离群值老猿暂还未完全弄明白,暂且存疑)
- 返回值:为仿射变换后的结果图像矩阵,最后的结果矩阵每个像素与原图像像素的对应关系为:
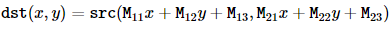
如果flags标记设置了WARP_INVERSE_MAP标记,首先使用invertAffineTransform对变换矩阵进行反转即求其逆矩阵,然后将其放入上面的公式中,而不是将M直接放入。例如如果变换矩阵是顺时针旋转30°,则设置WARP_INVERSE_MAP标记的情况下实际变换效果是逆时针旋转30°。这样做的目的是为了已知目标图像和变换方法的情况下,可以求出原图像。所以这个标记很重要 - 返回值:仿射变换后的结果图像
3.2、getRotationMatrix2D
getRotationMatrix2D用于获取一个旋转二维图像的仿射变换矩阵。
3.2.1、调用语法
getRotationMatrix2D(center, angle, scale)
3.2.2、参数语法说明
- center:图像旋转的旋转参考中心点坐标二元组
- angle:旋转角度,坐标原点为左上角情况下正值表示逆时针旋转
- scale:等比例缩放因子
3.2.3、返回值
getRotationMatrix2D返回值为一2*3复合旋转变换仿射矩阵。按照OpenCV官方介绍,getRotationMatrix2D得到的矩阵为:

在《https://blog.csdn.net/LaoYuanPython/article/details/113841635 图像仿射变换原理4:组合变换及对应变换矩阵》中介绍:
绕指定点旋转进行组合变换时,参考点p(m,n)顺时针旋转θ的组合变换的齐次坐标表示公式为:

上述公式中θ为正表示是顺时针旋转,与getRotationMatrix2D中的angle参数取值方式相反,由于cos(-θ)=cosθ,sin(-θ)=-sinθ,因此实际上getRotationMatrix2D中旋转正值的角度时对应的上述矩阵计算公式中sin函数前面的符号需要取反(正号变副号、副号变正号)。
而缩放的齐次坐标表示公式为:
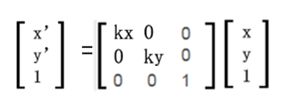
用缩放矩阵左乘平移矩阵则可以得到顺时针旋转同时进行缩放的齐次坐标表示公式:
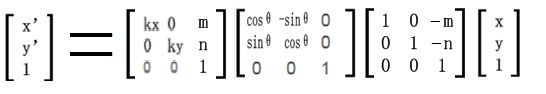
当等比例缩放且缩放因子等于s时,上述公式中的kx、ky使用s替换。则最后的组合变换矩阵为:

可以看到,将getRotationMatrix2D的参数angle(逆时针旋转为正)的角度变为上述组合矩阵变换公式中的-θ(顺时针旋转为正)、getRotationMatrix2D中的center.x、center.y分别使用m、n替换,取组合变换矩阵的前2行,则二者结果等价。因此getRotationMatrix2D函数获得的变换矩阵和上述组合变换矩阵连乘的结果相同。
3.3、getAffineTransform函数
getAffineTransform通过确认源图像中不在同一直线的三个点对应的目标图像的位置,来获取对应仿射变换矩阵,从而用该仿射变换矩阵对图像进行统一的仿射变换。
3.3.1、调用语法
retval = cv.getAffineTransform(src, dst)
3.3.1、语法说明
- src:源图像中三角形顶点的坐标,也就是在源图像中任找不在同一直线上的三个点,将三个点的坐标作为三个元素放到src对应列表中
- dst:目标图像中相应三角形顶点的坐标,也就是三个点在变换后图像中的坐标列表,要求与源图像三个点一一对应
- 返回值:从三对对应的点计算出来的仿射变换矩阵
四、案例:图像旋转
4.1、输入图像
图像文件名:f:\pic\dogAndCat.JPG,本图像比较大,所以装入后长和宽等比例缩小50%。

4.2、部分自定义函数说明
在使用自定义函数构造变换矩阵时,使用了在付费专栏文章《https://blog.csdn.net/LaoYuanPython/article/details/113879385 图像仿射变换原理5:组合变换矩阵的OpenCV-Python实现》介绍的如下自定义函数:
constructAffineMatrix(rotationAngle=0,xShearAngle=0,yShearAngle=0,translationX=0,translationY=0,scaleX=1,scaleY=1)
"""
:param rotationAngle: 旋转角度,图像旋转时使用,逆时钟为正、顺时针为负,如顺时针旋转30°,则值为-30
:param xShearAngle: 水平错切角,水平错切时使用
:param yShearAngle: 垂直错切角,垂直错切时使用
:param translationX: x轴平移距离
:param translationY: y轴平移距离
:param scaleX: 水平方向缩放因子
:param scaleY: 竖直方向缩放因子
:param bTMT: 是否返回3*3矩阵,为False返回2*3矩阵,为True返回3*3矩阵,默认值为False
:return: 构建的3*3矩阵
补充说明:
本函数只能构建旋转、错切、平移、缩放四种情况的一种矩阵,参数只取一种情况进行矩阵构造,
取的情况按照旋转、错切、平移、缩放从高到低的优先级排列,高优先级的值非0则低优先级的值忽略。
如果返回的矩阵为3*3矩阵,如果该矩阵立即调用warpAffine进行仿射变换,需要通过切片方式取前2行传入warpAffine,如果需要与其他仿射矩阵相乘,则必须保持3*3矩阵,相乘的结果再进行切片处理,因为两个2*3的矩阵之间没法相乘(矩阵乘法要求第一个矩阵的列数等于第二个矩阵的行数)
"""
matrixMultiply(*mList)#矩阵连乘函数,将输入的n个矩阵按从左到右方式相乘,返回结果矩阵
了解相关知识根据函数的说明自己实现以上函数并不难,且该部分仅在自定义实现仿射矩阵时需要,对仿射矩阵原理不感兴趣的可以忽略。
4.3、图像旋转案例
下面代码将图像读入后每按键一次在当前位置再逆时针旋转5°。使用两种方式实现,一种是直接使用OpenCV函数getRotationMatrix2D构建仿射矩阵,示例代码为函数rotationByOpenCVMat,一种是使用自定义函数构建仿射矩阵,示例代码为函数myrotation。
4.3.1 示例代码
def myrotation(imgfile):
img = cv2.imread(imgfile)
img = cv2.resize(img, None,fx=0.5, fy=0.5)
cv2.putText(img, 'https://blog.csdn.net/LaoYuanPython', (100, 158), fontFace=cv2.FONT_HERSHEY_SIMPLEX,fontScale=0.5, color=(255, 0, 0))
cv2.imshow('srcimg', img)
rows,cols,c = img.shape
#求原图像中心点
centerX = int(cols/2)
centerY = int(rows/2)
angle = 0 #初始角度
incAngle = 5 #每次增加角度
factor = 1 # 目标图像缩放因子,为了应对可能变换后图像范围扩大的情况如放到图像,为1表示不扩大
edge = int(sqrt(cols*cols+rows*rows)*factor) #目标图像边长设置为矩形的对角线长度,为了应对矩形绕中心旋转变换后图像范围扩大的情况
destCenter = int(edge / 2) #获取目标图像中心点
M1 = constructAffineMatrix(translationX=-1*centerX, translationY=-1 * centerY) #构建参考点(图像中心)平移到原点的平移矩阵
M3 = constructAffineMatrix(translationX=destCenter, translationY=destCenter) #构建参考点移动到目标图像中心位置的反向平移矩阵
flag = cv2.INTER_LINEAR #| cv2.WARP_INVERSE_MAP# | cv2.WARP_FILL_OUTLIERS
while True:
#复合变换矩阵 = 反向平移矩阵M3*旋转矩阵M2*平移矩阵M1
M2 = constructAffineMatrix(rotationAngle=angle) #构建基础旋转矩阵
M4 = np.matmul(M2,M1) #平移矩阵乘旋转矩阵
M = np.matmul(M3, M4) #再乘反向平移矩阵
M = matrixMultiply(M3,M2,M1) #构建复合旋转矩阵
dst1 = cv2.warpAffine(img, M[0:2], (edge,edge), flags=flag) #复合旋转变换
dst2= cv2.warpAffine(img, M2[0:2], (edge, edge), flags=flag) #基本旋转变换
cv2.imshow('rotationAndTranslation', dst1)
cv2.imshow('rotationOnly', dst2)
ch = cv2.waitKey(0)
if ch == 27:break
angle = (angle + incAngle) % 360 # 图像角度每次增加incAngle
cv2.destroyAllWindows()
def rotationByOpenCVMat(imgfile):
img = cv2.imread(imgfile)
img = cv2.resize(img,None,fx=0.5,fy=0.5)
cv2.putText(img, 'https://blog.csdn.net/LaoYuanPython', (100, 158), fontFace=cv2.FONT_HERSHEY_SIMPLEX,fontScale=0.5, color=(255, 0, 0))
rows, cols, c = img.shape
# 求原图像中心点
centerX = int(cols / 2)
centerY = int(rows / 2)
factor = 1 # 目标图像缩放因子,为了应对可能变换后图像范围扩大的情况如放到图像
edge = int(sqrt(cols * cols + rows * rows) * factor) # 目标图像边长设置为矩形的对角线长度,为了应对矩形绕中心旋转变换后图像范围扩大的情况,为1表示不扩大
destCenter = int(edge/2)
angle = 0 # 初始角度
incAngle = 5 # 每次增加角度
flag = cv2.INTER_LINEAR
while True:
M = cv2.getRotationMatrix2D((centerX,centerY),angle,1) # 构建复合旋转矩阵
dst = cv2.warpAffine(img, M, (edge,edge), flags=flag) # 复合旋转变换
cv2.imshow('rotationUsinggetRotationMatrix2D', dst)
ch = cv2.waitKey(0)
if ch == 27: break
angle = (angle + incAngle) % 360 # 图像角度每次增加incAngle
cv2.destroyAllWindows()
rotationByOpenCVMat(r'f:\pic\dogAndCat.JPG')
myrotation(r'f:\pic\dogAndCat.JPG')
由于图像是长方形的,以图像为中心的旋转过程会导致图像内容超出图像大小,因此在上述代码中将目标图像设置为了正方形,边长为原图像的对角线长度。
4.3.2、执行效果
- 使用rotationByOpenCVMat执行后效果
按键触发图像旋转,如下动图所示:
- 使用myrotation执行后绕目标图像中心旋转效果
- 使用myrotation执行后绕坐标原点旋转效果
从上述三张动图对比可以看出:
- rotationByOpenCVMat虽然放大了目标图像,但图像的内容并没有移动到目标图像的中间,导致放大后旋转还是有图像丢失,而使用myrotation执行后通过控制结果图像平移到目标图像中心,可以达到绕目标图像中心旋转且旋转过程中不丢失图像内容
- 使用myrotation执行后绕坐标原点旋转时,图像在旋转时可能完全超出目标图像范围导致不可见
- myrotation是顺时针旋转,rotationByOpenCVMat是逆时针旋转
五、案例2:任选三个点放大选定区域
详细案例请见《https://blog.csdn.net/LaoYuanPython/article/details/113924512 openCV仿射变换:getAffineTransform的案例》的介绍。
六、小结
本节介绍了仿射变换的概念、类型、基本仿射变换矩阵、OpenCV-Python与仿射变换相关的主要函数及语法说明,并提供了两种不同方式实现的图像旋转和任选三个点将圈定子图放大的示例。通过阅读相关内容可以有助于大家理解仿射变换的概念和仿射变换的OpenCV-Python实现方法。
七、后记
仿射变换涉及一些基础知识的理解如齐次坐标、变换矩阵,对于熟悉线性代数的人理解起来很容易,但对于未学过或者象老猿这种学过又还给老师的人来说则理解很困难,为此老猿花了40余天时间温习了部分线性代数知识,并查找各种资料,结合自己的理解写了如下仿射变换原理的博文:
- https://blog.csdn.net/LaoYuanPython/article/details/113743213 图像仿射变换原理1:齐次坐标来龙去脉详解
- https://blog.csdn.net/LaoYuanPython/article/details/113804210 图像仿射变换原理2:矩阵变换、线性变换和图像线性变换矩阵
- https://blog.csdn.net/LaoYuanPython/article/details/113788380 图像仿射变换原理3:仿射变换类型及变换矩阵详解
- https://blog.csdn.net/LaoYuanPython/article/details/113841635 图像仿射变换原理4:组合变换及对应变换矩阵
- https://blog.csdn.net/LaoYuanPython/article/details/113879385 图像仿射变换原理5:组合变换矩阵的OpenCV-Python实现
这些仿射变换原理方面的博文浓缩了仿射变换相关的基础知识,可以使得完全不了解仿射变换的人员理解仿射变换的基本原理和具体应用矩阵的构建,不过相关知识发布在了付费专栏,感兴趣的同仁可以订阅后阅读。
更多图像处理的介绍请参考专栏《OpenCV-Python图形图像处理 https://blog.csdn.net/laoyuanpython/category_9979286.html》和《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》相关文章。
更多图像处理的数学基础知识请参考专栏《人工智能数学基础 https://blog.csdn.net/laoyuanpython/category_10382948.html》
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
参考资料:
- [Python图像处理] 六.图像缩放、图像旋转、图像翻转与图像平移
关于老猿的付费专栏
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程,对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏,是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合,相关资料基本上都是老猿反复研究的成果,有助于OpenCV-Python初学者比较深入地理解OpenCV,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容,包括爬虫入门的基础知识,以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。
前两个专栏都适合有一定Python基础但无相关知识的小白读者学习,第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏:Python基础教程目录)从零开始学习Python。
如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。
![]()