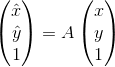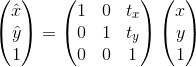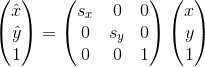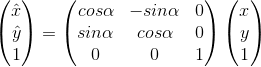OpenCV--Python 图像的几何变换（仿射变换【平移、放大、缩小、旋转、插值】、投影变换、极坐标变换）

目录

1.图像的仿射变换

1)平移

2)放大和缩小

3)旋转

4)计算仿射变换矩阵

5）插值算法

6）Python实现

2.图像的投影变换

3.极坐标转换

总结

---

首先要了解OpenCV的坐标原点(0,0)是在坐标的左上角，实现集合变换需要两个独立的算法：
    1.实现空间变换，描述每个像素如何从初始位置移动到终止位置
    2.差值算法，完成输出图像的每个像素的灰度值

1.图像的仿射变换

先来认识一个仿射变换公式

                                

为了表示方便，转换为矩阵就是下面的公式，其中A为仿射变换矩阵(以下都会用矩阵描述)：

                                       其中        

1)平移

如果要将任意空间坐标现沿x轴平移，再沿y轴平移，则最后得到的坐标为，用矩阵表示就是：

                                   

   如果为正，则向x轴正方向移动，如果为负，则向x轴负方向移动；同理。

2)放大和缩小

在二维坐标中，对图像进行缩放，其实就是对坐标距离进行缩放。
如果将(x,y)以(0,0)点在水平方向缩放倍，在垂直方向缩放倍，则。若>1，则表示在水平方向放大，<1，则表示在水平方向上缩小；同理。若=，则为同比例缩放。用矩阵表示为：

                                

如果将(x,y)以点在水平方向缩放倍，在垂直方向缩放倍，则。可以将变换过程理解为先将原点平移到中心点，再以原点为中心缩放，然后平移回坐标原点。用矩阵表示为：

            

需要注意的是，等式右边的计算是从右向左进行的(后边的雷同)。

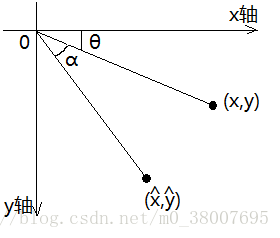
3)旋转

              

如果(x,y)以原点(0,0)为中心按逆时针旋转到，由上图可知，，其中p表示(x,y)到中心点(0,0)的距离。

矩阵形式表示为：

                     

如果是按照顺时针旋转，则矩阵(自己推一遍)可表示为：

                    

从得到的两个旋转仿射矩阵可知，若以一个方向为正方向，其实两个矩阵是一样的。

以上是以(0,0)为中心进行旋转的，如果(x,y)绕任意一点逆时针旋转角度α，则首先将原点移到旋转中心，然后按照原点旋转，最后移回坐标原点，矩阵表示为：

             

4)计算仿射变换矩阵

以上解决的都是已知坐标及其仿射变换矩阵，从而计算出变换后的坐标。下面通过已知坐标及其对应的经过某种仿射变换后的坐标，从而计算出他们之间的仿射变换矩阵。

1.方程法：仿射变换矩阵有六个未知参数，所以只需要三组对应坐标，构造出由六个方程组成的方程组即可解出六个未知数。OpenCV提供的函数 cv2.getAffineTransform(src, dst)就是通过方程法计算参数 src 到 dst 对应仿射变换矩阵的。其 src 和 dst 分别代表原坐标和变换后的坐标，且均为3行2列的二维ndarray，每一行代表一个坐标，且数据类型必须为浮点型，否则会报错。

import cv2 as cv
import numpy as np
src = np.array([[0, 0], [200, 0], [0, 200]], np.float32) # 源图像坐标
dst = np.array([[0, 0], [100, 0], [0, 100]], np.float32) # 转换后图像坐标
A = cv.getAffineTransform(src, dst)
print(A)
'''
结果为：
[[ 0.5  0.   0. ]
 [ 0.   0.5  0. ]]
'''

2.矩阵法：对于使用矩阵相乘法计算仿射矩阵，前提是需要知道基本仿射变换步骤(这里不再进行详述)。

介绍一个OpenCV提供的函数 cv2.getRotationMatrix2D(center, angle, scale)，这个函数是针对等比例缩放求出仿射变换矩阵
参数：
    center: 变换中心点的坐标
    scale: 等比例缩放的系数
    angle: 逆时针旋转的角度(若为负数，则为顺时针；单位为角度，不是弧度)

import cv2 as cv
import numpy as np
A = cv.getRotationMatrix2D((40, 50), 30, 0.5)
print(A.dtype)
print(A)
'''
结果为：
float64
[[  0.4330127    0.25        10.17949192]
 [ -0.25         0.4330127   38.34936491]]
'''

5）插值算法

在对图像进行变换的时候，变换后的图像的像素位置可能在原图像上没有对应的像素存在(因为像素的坐标位置只有整数，没有小数)。比如将一个图像进行2倍放大，放大后的图像的像素位置(3,3)在原图像上没有像素所对应，只有偶数的有对应。这时，我们就需要插值算法来决定这个像素由原图像的哪个位置的像素来代替。

1.最近邻插值：设(x,y)为转换后的图像对应原图像的坐标，则最近邻插值就是从(x,y)的四个相邻整数坐标中找到离它最近的一个，将此位置的像素作为转换后图像的像素。举个例子，(2.3, 4.7) 的四个相邻整数坐标分别为(2, 4)、(2, 5)、(3, 4)、(3, 5)，离它最近的是(2, 5)，则将(2.3, 4.7)所对应的坐标位置的像素用原图像的(2, 5)坐标位置的像素代替。

使用最近邻插值方法完成图像几何变换，输出图像会出现锯齿状外观，对图像放大处理的效果会更明显。为了得到更好的效果，应使用更多的信息，而不仅仅使用最近像素的灰度值，常用的方法是双线性插值和三次样条插值。

2.双线性插值

对于一个目的像素，设置坐标通过反向变换得到的原图像的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分，u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定，即：
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)                          
其中f(i,j)表示源图像(i,j)处的的像素值，以此类推。

比如，现在假如目标图的像素坐标为（1，1），若反推得到的对应于源图的坐标是（0.75 , 0.75）, 这其实只是一个概念上的虚拟像素,实际在源图中并不存在这样一个像素,那么目标图的像素（1，1）的取值不能够由这个虚拟像素来决定，而只能由源图的这四 个像素共同决定：（0，0）（0，1）（1，0）（1，1），而由于（0.75,0.75）离（1，1）要更近一些，那么（1,1）所起的决定作用更大一 些，这从公式1中的系数uv=0.75×0.75就可以体现出来，而（0.75,0.75）离（0，0）最远，所以（0，0）所起的决定作用就要小一些， 公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点。

3.三次样条插值

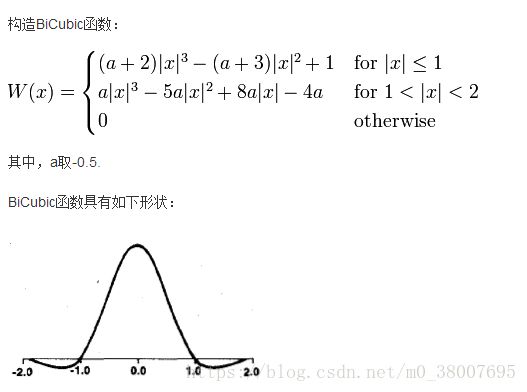
在双线性插值是选取了目标像素坐标周围的四个点，在三次样条插值中选取目标像素坐标周围的16个点来共同决定该坐标的像素值。他们的权重是根据函数BiCubic来确定的：

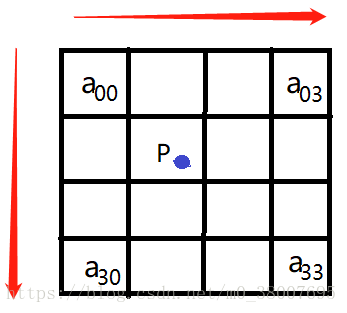
其中BiCubic函数中的x代表的是目标像素坐标与周围的16个像素坐标的距离(包括x轴距离和y轴距离)，总共有4个x轴距离和4个y轴距离。将这些距离带入W()函数中得到相应像素点的权重，再将周围16个点的像素值*W(x轴的距离)*W(y轴的距离)，并进行求和得到目标坐标对应的像素值。

以下图为例，假设P点坐标为(2.7, 4.8)，则横轴的距离依次为1.7, 0.7, 0.3, 1.3（分别以,,,来表示），纵轴的距离依次为1.8, 0.8, 0.2, 1.2(分别以,,,来表示)，得到这些距离带入W()函数中就得到了权重。以f(p)表示p的像素值，则此时P的像素值为：

               

其中i代表的是行数，j代表的是列数，代表的与像素点P的垂直距离，代表的是与像素点P的水平距离。

 

6）Python实现

在已知仿射变换矩阵的基础上，OpenCV提供了函数来实现仿射变换：
cv2.warpAffine(src, M, size[, dst[, flags[, borderMode[, borderValue]]]])
参数：
    src: 输入图像矩阵
    M: 2行3列的仿射变换矩阵
    dsize: 二元元组(宽，高)，输出图像的大小
    flags: 插值法：INTER_NEAREST、INTER_LINEAR、INTER_CUBIC等
    borderMode: 填充模式：BORDER_CONSTANT等
    borderValue: 当borderMode=BORDER_CONSTANT时的填充值
关于更详细的参数说明可到官网查看，以下通过简单的代码示例函数的使用：

import cv2 as cv
import numpy as np
img = cv.imread("../images/er.jpg")
# 原图的高、宽
h, w = img.shape[:2]
# 仿射变换矩阵，缩小2倍
A1 = np.array([[0.5, 0, 0], [0, 0.5, 0]], np.float32)
d1 = cv.warpAffine(img, A1, (w, h), borderValue=0)
# 先缩小2倍，再平移
A2 = np.array([[0.5, 0, w / 4], [0, 0.5, h / 4]], np.float32)
d2 = cv.warpAffine(img, A2, (w, h), borderValue=0)
# 在d2的基础上，绕图像的中心点旋转
A3 = cv.getRotationMatrix2D((w / 2.0, h / 2.0), 30, 1)
d3 = cv.warpAffine(d2, A3, (w, h), borderValue=0)
# 如果要选择插值的方法可以通过参数flags设置，如flags=cv.INTER_CUBIC

cv.imshow("img", img)
cv.imshow("d1", d1)
cv.imshow("d2", d2)
cv.imshow("d3", d3)
cv.waitKey()
cv.destoryAllWindows()

运行结果如下图：

(a)原图                                  (b)缩小                                           (c)缩小+平移                 (d)缩小+平移+旋转

使用函数warpAffine对图像进行缩放，需要先创建仿射变换矩阵。为了使用更加方便，对于图像的缩放，OpenCV还提供了另一个函数：cv.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]]) 来实现，其参数解释如下：

参数	解释
src	输入图像矩阵
dsize	输出图像矩阵
dst	二元元组(宽，高)，输出图像的大小
fx	在水平方向的缩放比例，默认为0
fy	在垂直方向的缩放比例，默认为0
interpolation	插值法：INTER_NEAREST，INTER_LINEAR等

在OpenCV 3.X中提供了一个简单的函数来实现图片的90，180，270度的旋转： 
cv2.rotate(src, rotateCode)
参数rotateCode: ROTATE_90_CLOCKWISE,顺时针旋转90度
                           ROTATE_180,顺时针旋转180度
                           ROTATE_90_COUNTERCLOCKWISE,顺时针旋转270度
注意：虽然是图像矩阵的旋转，但该函数不需要利用仿射矩阵变换来完成这类旋转，只是行列的互换，类似于矩阵的转置操作。

下面使用Python程序来实现两种旋转：

import cv2 as cv
import numpy as np
img = cv.imread("../images/er.jpg")
h, w = img.shape[:2]
# 图像旋转：cv2.ROTATE_180,cv2.ROTATE_90_COUNTERCLOCKWISE
rota = cv.rotate(img, cv.ROTATE_90_COUNTERCLOCKWISE)
# 仿射变换矩阵的方式
A = cv.getRotationMatrix2D((h / 2.0, w / 2.0), 90, 1)
rota2 = cv.warpAffine(img, A, (w, h))
cv.imshow("img", img)
cv.imshow("rotate", rota)
cv.imshow("rotate2", rota2)
cv.waitKey()
cv.destoryAllWindows()

2.图像的投影变换

在对仿射变换的讨论中，校正物体都是在二维空间中完成的，如果物体在三维空间中发生的旋转，那么这种变换通常被称为投影变换。由于可能出现阴影或遮挡，所以此投影变换是很难修正的。但是如果物体是平面的，那么就能通过二维投影变换对此物体三维变换进行模型化，这就是专用的二维投影变换，可由如下公式描述：

与方程法计算仿射变换矩阵的函数 getAffineTransform() 类似，OpenCV提供了函数：
cv2.getPerspectiveTransform(src, dst)
        src: 原坐标，4x2的二维ndarray，其中每一行代表一个坐标，float32
        dst: 变换后的坐标，4x2的二维ndarray，其中每一行代表一个坐标，float32

import cv2 as cv
import numpy as np
src = np.array([[0, 0], [200, 0], [0, 200], [200, 200]], np.float32)
dst = np.array([[100, 20], [200, 20], [50, 70], [250, 70]], np.float32)
P = cv.getPerspectiveTransform(src, dst)
print(P.dtype)
print(P)
'''
float64
[[  5.00000000e-01  -3.75000000e-01   1.00000000e+02]
 [  3.88578059e-16   7.50000000e-02   2.00000000e+01]
 [  9.54097912e-18  -2.50000000e-03   1.00000000e+00]]
'''

类似于仿射变换，OpenCV提供了函数  cv2.warpPerspective(src, M, size[, dst[, flags[, borderMode[, borderValue]]]]) 来实现投影变换功能，其使用方法和参数也与 cv2.warpAffine() 相似。对图像的投影变换代码如下：

import cv2 as cv
import numpy as np
img = cv.imread("../images/er.jpg")
h, w = img.shape[:2]
src = np.array([[0, 0], [w - 1, 0], [0, h - 1], [w - 1, h - 1]], np.float32)
dst = np.array([[50, 50], [w / 3, 50], [50, h - 1],
                [w - 1, h - 1]], np.float32)
# 计算投影变换矩阵
p = cv.getPerspectiveTransform(src, dst)
# 利用计算出的投影变换矩阵进行图像的投影变换
r = cv.warpPerspective(img, p, (w, h), borderValue=0)
# 显示原图和投影效果
cv.imshow("img", img)
cv.imshow("warp", r)
cv.waitKey()

3.极坐标转换

通常利用极坐标变换来校正图像中的圆形物体或被包含在圆环中的物体。

1)将笛卡尔坐标转换为极坐标

笛卡尔坐标系 xoy 平面上的任意一点 (x,y)，以  为中心，可以得到极坐标系  上的极坐标 。OpenCV提供了函数：
cartToPolar(x, y[, magnitude[, angle[, angleInDegrees]]])
        x: array数组且数据类型为浮点型、float32或者float64
        y: 和x具有相同尺寸和数据类型的array数组
        angleInDegrees: 当值为True时，返回值angle是角度；反之，为弧度
返回值：manitude、angle是与参数x和y具有相同尺寸和数据类型的ndarray

举例：计算(0,0),(1,0),(2,0),(0,1),(1,1),(2,1),(0,2),(1,2),(2,2)这九个点以(1,1)为中心进行的极坐标变换。首先将坐标原点移动到(1,1)处，按照平移仿射矩阵计算出这9个点平移后的坐标值，然后利用cartToPolar()进行极坐标变换。代码如下：

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[0, 1, 2], [0, 1, 2], [0, 1, 2]], np.float64)
y = np.array([[0, 0, 0], [1, 1, 1], [2, 2, 2]], np.float64)
r, theta = cv.cartToPolar(x - 1, y - 1, angleInDegrees=True)
print(r)
print(theta)
'''
[[ 1.41421356  1.          1.41421356]
 [ 1.          0.          1.        ]
 [ 1.41421356  1.          1.41421356]]
[[ 224.99045634  270.          315.00954366]
 [ 180.            0.            0.        ]
 [ 135.00954366   90.           44.99045634]]
'''

这几个点变换前与变换后大概是这样分布的(在转换前，点5为圆心，点2,4,6,8在同一个圆上，点1,3,7,9在同一个圆上)：

2)将极坐标转换为笛卡尔坐标

OpenCV提供了函数 polarToCart(magnitude, angle[, x[, y[, angleInDegrees]]]) 来实现将极坐标转换为笛卡儿坐标，其参数解释与函数cartToPolar()类似。注意：返回的是以原点(0,0)为中心的笛卡儿坐标。

举例：已知极坐标系 中的(30,10), (31,10), (30,11), (31,11) ，其中是以角度表示的，问笛卡儿坐标系xoy中的哪四个坐标以(-12,15)为中心经过极坐标变换后得到这四个坐标，实现代码如下：

import cv2 as cv
import numpy as np
angle = np.array([[30, 31], [30, 31]], np.float32)
r = np.array([[10, 10], [11, 11]], np.float32)
x, y = cv.polarToCart(r, angle, angleInDegrees=True)
# 此处得到的x,y是以(0,0)为变换中心的，而这里的变换中心为(-12,15)
# 所以只要进行以下操作即可得到对应的笛卡儿坐标
x += -12
y += 15
print(x)
print(y)
'''
[[-3.33974457 -3.42832565]
 [-2.4737196  -2.57115746]]
[[ 20.          20.150383  ]
 [ 20.5         20.66542053]]
'''

3)利用极坐标变换对图像进行变换

import cv2 as cv
import numpy as np

def polar(I, center, r, theta=(0, 360), rstep=1.0, thetastep=360.0 / (180 * 8)):
    '''
    参数
        I：输入图像
        center：极坐标的变换中心
        r：二元元组，最小距离和最大距离
        theta：角度范围，默认[0, 360]
        rstep：r的变换步长，默认1
        thetastep：角度的变换步长，默认1/4
    '''
    # 拿到原始图像的高和宽
    h, w = I.shape[:2]
    # 极坐标的中心
    cx, cy = center
    # 得到距离的最小、最大范围
    minr, maxr = r
    # 角度的最小范围
    mintheta, maxtheta = theta
    # 输出图像的高、宽
    H = int((maxr - minr) / rstep) + 1
    W = int((maxtheta - mintheta) / thetastep) + 1
    O = np.ones((H, W, 3), I.dtype)
    # 极坐标变换
    r = np.linspace(minr, maxr, H)
    r = np.tile(r, (W, 1))
    r = np.transpose(r)
    theta = np.linspace(mintheta, maxtheta, W)
    theta = np.tile(theta, (H, 1))
    x, y = cv.polarToCart(r, theta, angleInDegrees=True)
    # 最近邻插值
    for i in range(H):
        for j in range(W):
            px = int(round(x[i][j] + cx))
            py = int(round(y[i][j] + cy))
            if((px >= 0 and px <= w - 1) and (py >= 0 and py <= h - 1)):
                # print(px, py)
                O[i][j] = I[py][px]
    return O

img = cv.imread("../images/circle2.jpg")
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# h, w = img.shape[:2]
# 极坐标变换中心
cx, cy = 248, 252
# cv.circle(img, (int(cx), int(cy)), 210, (255, 0, 0), 3)
# cv.circle(img, (int(cx), int(cy)), 70, (255, 0, 0), 3)
# 距离的最小、最大半径 # 150 250
O = polar(img, (cx, cy), (70, 210))
# 旋转
O = cv.flip(O, 0)
# 显示
cv.imshow("img", img)
cv.imshow("O", O)
cv.waitKey()

其中用到了函数 cv.circle(img, center, radius, color, thickness=1, lineType=8)，img代表输入图像，center代表圆心，radius代表圆的半径，color代表画出的圆的颜色，thickness代表线的粗细，linesType代表线的类型。OpenCV还提供了函数rectangle、ellipse、line分别用于在图中画矩形、椭圆形和线段这些基本的几何形状，使用方法与circle类似。以上代码的显示结果为：

在以上程序中还使用了函数 cv2.flip(src, flipCode[, dst]) 进行处理，实现了矩阵的水平镜像、垂直镜像及逆时针旋转180度，其中逆时针旋转180度也可以理解为先将矩阵进行水平镜像处理，然后进行垂直镜像处理。参数解释如下：
      src: 输入图像矩阵
      dst: 输出图像矩阵，其尺寸和数据类型与src相同
      flipCode: >0,src绕y轴的镜像处理
                     =0,src绕x轴的镜像处理
                     <0,src逆时针旋转180度

4)线性极坐标函数linearPolar(OpenCV 3.X特性)

cv2.linearPolar(src, center, maxRadius, flags[, dst])

参数	解释
src	输入图像矩阵(单、多通道矩阵都可以)
dst	输出图像矩阵，其尺寸和src是相同的
center	极坐标变换中心
maxRadius	极坐标变换的最大距离
flags	插值算法，同函数resize, warpAffine的插值算法

import numpy as np
import cv2 as cv
img = cv.imread("../images/circle2.jpg")
cv.imshow("img", img)
dst = cv.linearPolar(img, (248, 252), 210, cv.INTER_LINEAR)
cv.imshow("dst", dst)
cv.waitKey()

函数linearPolar生成的极坐标，在垂直方向上，r在水平方向上。此函数有两个缺点：1.极坐标变换的步长是不可控制的，导致得到的图可能不是很理想；2.该函数只能对整个圆内区域，而无法对一个指定的圆环区域进行极坐标变换。

5)对数极坐标函数logPolar (OpenCV 3.X特性)

dst=cv.logPolar(src, center, M, flags[, dst])

参数	解释
src	输入图像矩阵(单、多通道矩阵都可以)
dst	输出图像矩阵，其尺寸和src相同
center	极坐标变换中心
M	系数，该值大一点效果会好一些
flags	WARP_FILL_OUTLIERS，笛卡儿坐标向对数极坐标变换 WARP_INVERSE_MAP，对数极坐标向笛卡儿坐标变换

import numpy as np
import cv2 as cv
img = cv.imread("../images/circle2.jpg")
cv.imshow("img", img)
M1 = 50
M2 = 100
M3 = 150
dst1 = cv.linearPolar(img, (248, 252), M1, cv.WARP_FILL_OUTLIERS)
dst2 = cv.linearPolar(img, (248, 252), M2, cv.WARP_FILL_OUTLIERS)
dst3 = cv.linearPolar(img, (248, 252), M3, cv.WARP_FILL_OUTLIERS)
cv.imshow("dst1", dst1)
cv.imshow("dst2", dst2)
cv.imshow("dst3", dst3)
cv.waitKey()

下图为程序显示结果，分别取M=50、100、150，可以看出M值越大，在水平方向得到的信息越多。

 

总结

用到的函数都有：
仿射变换：getAffineTransform()、getRotationMatrix2D()、warpAffine()、rotate()、resize()
投影变换：getPerspectiveTransform()、warpPerspective()
极坐标转换：cartToPolar()、polarToCart()、linearPolar()、logPolar()