数据结构之树(4)——红黑树
目录
红黑树
概念
调整
变色
左旋和右旋
插入
插入情况分析
插入平衡总结
插入实例
删除
概述
删除情况分析
删除平衡总结
删除实例
参考链接
红黑树
概念
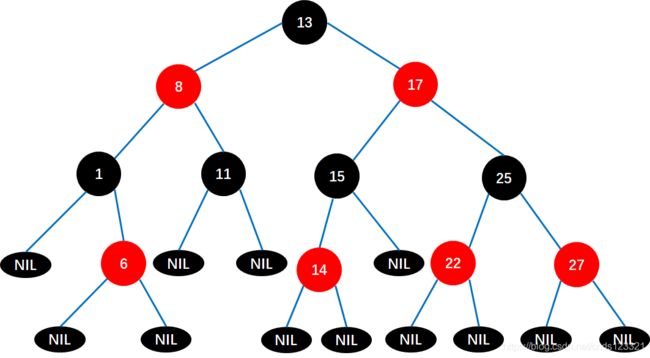
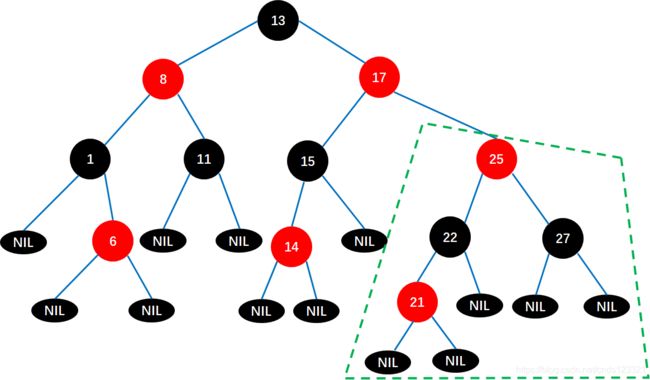
红黑树同样是解决二叉排序树不平衡的问题的,例如下面这种失衡的二叉树。
所以红黑树首先是一棵二叉排序树,然后是二叉平衡树的特殊形式。
![]()
红黑树(Red Black Tree)是一种自平衡的二叉查找树。红黑树有如下特性:
- 结点是红色或者黑色的。
- 根结点是黑色的。
- 每个叶子结点都是黑色的空结点(NIL结点)。
- 每个红色结点的两个子结点都是黑色的(从每个叶子到根的所有路径上不能有两个连续的红色结点)。
- 从任一结点到其每个叶子的所有路径都包含相同数组的黑色结点。
调整
新插入的结点颜色一定要先设置为红色,下面向红黑树种插入一个值为14的结点。
符合红黑树的规则,不需要调整平衡。
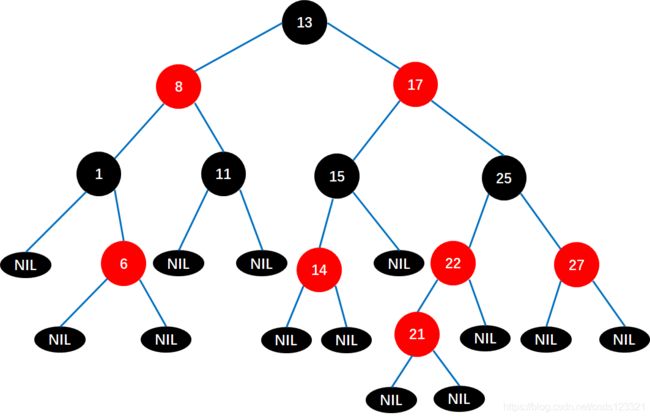
再插入一个21结点,如下图:
违反了上面的“每个红色结点的两个子结点都是黑色的”,所以必须进行调整,让这棵树重新符合红黑树的定义。
叶子(NIL)节点就是一个空节点,表示节点在此位置上没有元素了。在实际的算法实现中NIL不需要考虑,填上NIL节点只是为了判断到此路径终点的NIL节点上,经过多少黑节点。
调整红黑树有两种方法:变色和旋转(左旋转和右旋转)
- 变色:将红色结点变为黑色,或者将黑色结点变为红色。
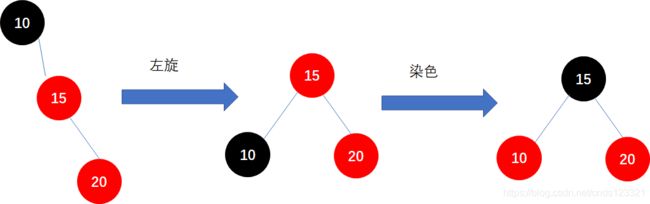
- 左旋转:逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。
- 右旋转:顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。
变色
下面说下变色:
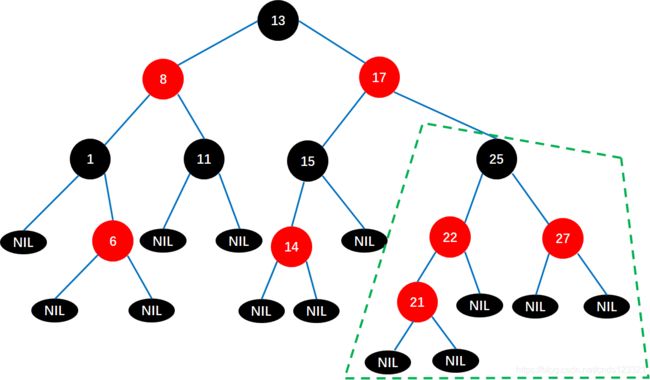
结点21和结点22都是红色,需要进行调整
将结点22变成黑色
但又不符合“从任一结点到其每个叶子的所有路径都包含相同数组的黑色结点”规则,从根结点13到结点21下的NIL结点,共有4个黑色结点,其他路径有3个黑色结点。
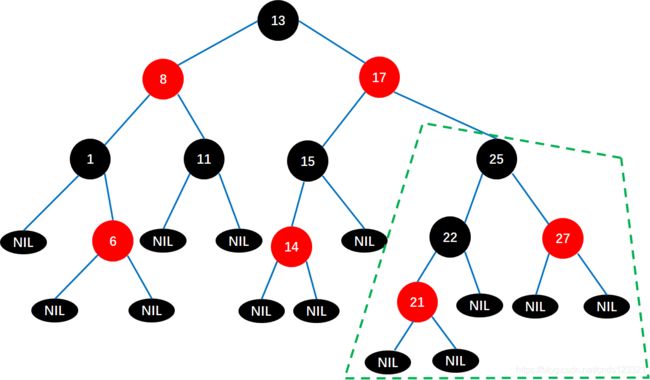
所以将结点25变成红色结点,如下:
此时发现结点25和结点27都是红色结点,所以将结点27变为黑色结点。
总之,变色就是改变结点的颜色,要么是红色,要么是黑色,然后调整成符合红黑树的规则。
左旋和右旋
关于左旋和右旋可以查看AVL树中的旋转:数据结构之树(3)——二叉平衡树(AVL)
左旋转,在上面已经说了
![]()
右旋转,上面也讲了的
![]()
但什么时候用变色,什么时候又用旋转呢,这很复杂,红黑树的插入和删除都需要判断调整是否符合红黑树的规则,然后调整。
下面通过其他参考资料来试图说明下红黑树插入和删除的各种情况:
插入
插入情况分析
红黑树的插入同二叉排序树的插入过程相似,但红黑树插入新结点后,需要判断红黑树是否符合定义要求,如果不符合,租需要进行调整,以满足红黑树的性质。
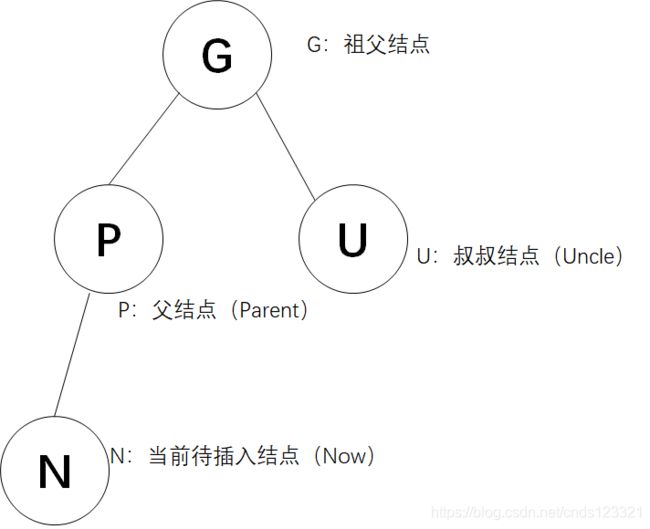
认识下结点的标记
第一种情况:如果插入的结点是根结点,那么该结点颜色调整为黑色
但发现不满足“根结点是黑色的”,所以需要调整,将根结点调整为黑色。
![]()
这时发现红黑树的所有要求被满足。
第二种情况:待插入结点的父结点是黑色,不需要调整
第三种情况:待插入结点的父结点是红色,同时叔叔结点也是红色,需要调整
发现新插入的结点N和父结点P是连续红色,需要调整红黑树。
调整方法:将父亲结点P和叔叔结点U重新绘制为黑色,祖父结点G绘制为红色。但是,如果此处祖父结点G为根节点,那么需要调用红黑树修正程序,将祖父结点绘制为黑色,如果祖父结点G被染成红色后,可能和它的父结点形成连续的红色结点,此时需要递归向上调整。
第四种情况:待插入结点的父结点是红色,同时叔叔结点是黑色,需要调整
在满足父节点是红色,叔叔节点是黑色的条件下,又可以分以下几种情况:
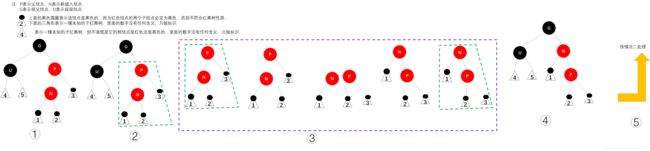
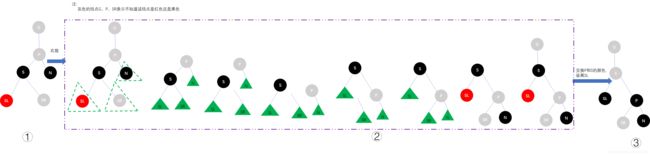
- 情况一:父结点P是祖父结点G的左子结点,待插入结点N是父结点的左子结点
调整方法:以祖父结点G为支点进行右旋,然后将父结点P染黑,祖父结点G染红。
说明:
- ①表示新插入结点N后,红黑树失衡,需要调整连续的红色结点N和P。
- ②不重要,将N和U及其子树当作一个整体,促成右旋转的形式,为右旋转做准备。
- ③不重要,这其实就是右旋转的过程,一步步拆分来的。
- ④不重要,将当成整体的绿色三角形N和U再次组装成完整的,即右旋转完成后的结果。
- ⑤对父结点P染成黑色,祖父结点G染成红色,这是最后一步,其实网上的资料只有①和⑤两步,这里只是把每一个步骤都拆分了。
下面说第二种情况。
- 情况二:父结点P是祖父结点的右子结点,待插入结点N是父结点P的右子结点
调整方法:以祖父结点G为支点进行左旋,然后将父结点P染黑,祖父结点染红。
说明:
- ①表示新插入结点N后,红黑树失衡,需要调整连续的红色结点N和P。
- ②不重要,将N和U及其子树当作一个整体,促成右旋转的形式,为右旋转做准备。
- ③不重要,这其实就是左旋转的过程,一步步拆分来的。
- ④不重要,将当成整体的绿色三角形N和U再次组装成完整的,即右旋转完成后的结果。
- ⑤对父结点P染成黑色,祖父结点G染成红色,这是最后一步,其实网上的资料只有①和⑤两步,这里只是把每一个步骤都拆分了。
下面说明第三种情况。
情况三:父结点P是祖父结点的左子结点,待插入结点N是父结点P的右子结点
调整方法:以父结点P为支点进行左旋,然后做情况一处理。
说明:
- ①表示失衡的情况,需要进行调整。
- ②单独把以P为根结点的子树提取出来,当成一个分支来处理。
- ③将绿色框内的子树以P结点为支点进行左旋转,紫色框内是左旋转的步骤,每一步分开来的。
- ④将旋转完成的分支组合到②中
- ⑤此时的情况与“情况一”中一致,使用情况一中的调整方法进行调整即可。
下面说明第四种情况。
情况四:父结点P是祖父结点G的右子结点,待插入结点N是父结点的左子结点
调整方法:以父结点P为支点进行右旋转,旋转后,然后做情况二处理。
说明:
- ①表示失衡的情况,需要进行调整。
- ②单独把以P为根结点的子树提取出来,当成一个分支来处理。
- ③将绿色框内的子树以P结点为支点进行右旋转,紫色框内是右旋转的步骤,每一步分开来的。
- ④将旋转完成的分支组合到②中
- ⑤此时的情况与“情况二”中一致,使用情况二中的调整方法进行调整即可。
插入平衡总结
红黑树插入元素总结:
插入实例
实例:用如下序列{10,20,15,30,5,8}绘制红黑树
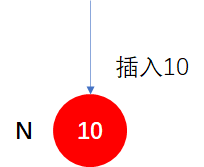
第一步:插入10,由于是第一个插入的结点,所以是根结点
按照上面的总结,需要将N染黑。
第二步:插入20
![]()
根据上面的总结,父结点为黑色,不需要调整。
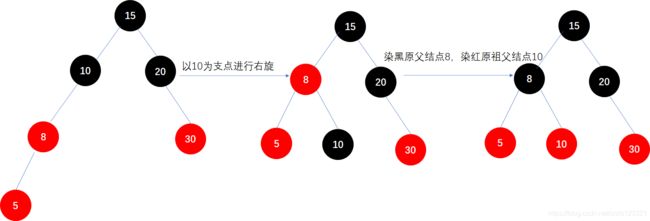
第三步:插入15
根据上面的总结,N的父结点P是红色,N的叔叔结点没有,所以是第四种情况,但父结点20是祖父结点10的右子结点,N结点15是父结点20的左子,所以是情形四,故先以父结点20为支点进行右旋。
现在以20为N结点,然后结点20的父结点15是红色,没有叔叔结点,同时父结点20是祖父结点10的右子结点,N结点20是父结点15的右子,满足“情形二”,所以调整是以祖父结点10为支点进行左旋,染黑原父结点15,染红原祖父结点10。
所以整理并染色如下:
第四步:插入30
现在N结点是30,N的父结点20是红色,N的叔叔结点10也是红色,所以满足第三种情况,所以调整的方法是染黑父结点20和叔叔结点10,并且染红祖父结点15.。
发现根结点15是红色的,不符合红黑树要求,所以将根结点染黑。
第五步:插入5
现在N结点是5,N结点的父结点是黑色,所以不需要进行调整红黑树。
第六步:插入8
现在N结点是8,N结点的父结点5是红色结点,N结点没有叔叔结点,所以是第四种情况,同时父结点5是祖父结点10的左子结点,N是父结点5的右子结点,所以是情形三。
以父结点5为支点进行左旋。
现在N结点是5,由于父结点8是祖父结点10的左子结点,N是父结点8的左子结点,所以调整红黑树的方式是以祖父结点10右旋,染黑原父结点8,染红原祖父结点10。
删除
概述
删除红黑树结点的操作分为查找到要被删除的结点,然后就是删除该结点即可,最麻烦的就是删除结点后重新维持红黑树平衡的问题。
删除结点有3种情景:
- 第一种:若删除结点没有子结点,直接删除。
- 第二种:若删除结点只有一个子结点,用子结点替换删除结点。
- 第三种:若删除结点有两个子结点,同二叉搜索树一样,用后继结点(要么是它的左子树中的最大元素,要么是它的右子树的最小元素)替换删除结点。
删除的三种情况其实根二叉排序树的删除是一样的,因为红黑树首先是一棵二叉排序树。
所以可以参考:数据结构之树(2)——二叉查找树和二叉排序树
先要约定下结点名称:
删除结点后就会面临一个情况:红黑树是否还平衡?如果平衡则不需要进行调整,否则需要进行调整。
平衡是在删除黑色叶子结点后才发生的操作,比如P->D->N,删除黑色结点D后,变成P->N,导致经过N的路径的黑色结点数量减少1个,所以需要进行平衡处理。
删除情况分析
调整删除结点后的红黑树平衡有如下几种情况:
第一种情况:结点N是根结点,无需调整
当删除的结点是根结点,那么无需调整平衡,因为所有路径都少一个黑色结点,仍然保持平衡。例如:
第二种情况:兄弟结点S是黑色的
但在该种情况下又分为好几种不同情形:
- 情况一:兄弟结点S的所有子结点都是黑色,即SR和SL都是黑色的。
又分为两种情形:父结点P是红色还是黑色?
下面来处理父结点P是红还是黑的情况:
-
- 情形一:父结点P为黑色
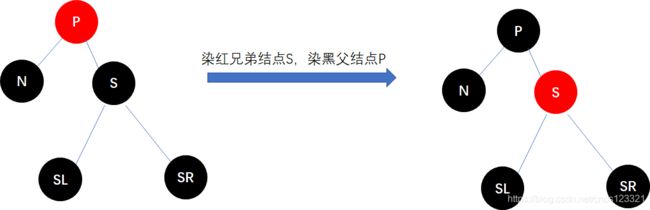
调整方法:染红兄弟结点S,将父结点P作为新的N结点,递归处理。
为什么需要递归处理?
-
- 情形二:父结点P为红色
调整方法:染红兄弟结点S,染黑父结点P,平衡完成。
- 情况二:兄弟结点S的子结点不全黑。
不全黑包括3种情况:SL黑SR红、SL红SR黑、SL红SR红。所以得出结论:如果其中一个为黑,另外一个肯定是红。
之所以以全黑与不全黑进行分类,因为兄弟结点S可能是父结点P的左子结点,也可能是右子结点。如果是全黑,那么兄弟结点S无论是左子结点还是右子结点,处理方式一样;但如果不是全黑,那么就要看兄弟结点S所处的位置,进行特定方向的旋转。
-
- 情形一:兄弟结点S是父结点P的左子结点,SL结点红色,SR结点颜色未知
调整方法:以父结点P为支点进行右旋,交换父结点P和兄弟结点S的颜色,染黑兄弟结点的左子结点SL,平衡完成。
其中完整的过程是:
- ①不平衡的红黑树,待调整进行平衡。
- ②对不平衡的红黑树进行右旋操作,以父结点P为支点进行右旋,里面是右旋的每一步具体步骤。
- ③交换P和S的颜色,染黑SL,这里是不知道SR、P、G结点的颜色的,也不在乎。
-
- 情形二:兄弟结点S是父结点P的右子结点,SR结点红色,SL结点颜色未知
与上面的情形一呈镜像关系,所以调整方法:以父结点P为支点进行左旋,旋转后,交换P和S颜色,结点SR染黑。
其中完整的过程是:
- ①不平衡的红黑树,待调整进行平衡。
- ②对不平衡的红黑树进行左旋操作,以父结点P为支点进行左旋,里面是左旋的每一步具体步骤,如果不明白是如何左旋的,可能查看步骤,否则直接看上面那张图即可,里面的绿色三角形都是辅助完成左旋操作的,实际上只是为了方便理解,并无实际应用。
- ③交换P和S的颜色,染黑SR,这里是不知道SL、P、G结点的颜色的,也不在乎。
-
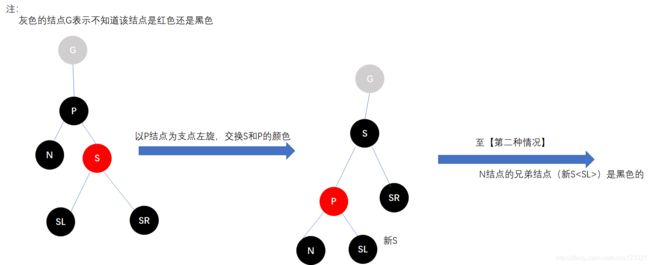
- 情形三:兄弟结点S是父结点P的左子结点,SL结点黑色,SR结点一定是红色的。
调整方法:以兄弟结点S进行左旋,旋转后,交换结点S和SR的颜色,最后转至【情况二-情形一】处理。
旋转完整流程如下:
- ①不平衡的红黑树,待调整进行平衡。
- ②对不平衡的红黑树进行左旋操作,以兄弟结点S为支点进行左旋,里面是左旋的每一步具体步骤,如果不明白是如何左旋的,可能查看步骤,否则直接看下面那张图即可,里面的绿色三角形都是辅助完成左旋操作的,实际上只是为了方便理解,并无实际应用。
- ③交换S和SR的颜色。
- ④转至【情况二-情形一】处理,此时SR结点是新的S结点,S结点是新的SL结点。
-
- 情形四:兄弟结点S是父结点P的右子结点,SL结点红色,SR结点是黑色的。
调整方法:以兄弟结点S为支点进行右旋,旋转完成后,交换S和SL的颜色,然后转至【情况二-情形二】
旋转完整流程如下:
- ①不平衡的红黑树,待调整进行平衡。
- ②对不平衡的红黑树进行右旋操作,以兄弟结点S为支点进行右旋,里面是右旋的每一步具体步骤,如果不明白是如何右旋的,可能查看步骤,否则直接看下面那张图即可,里面的绿色三角形都是辅助完成右旋操作的,实际上只是为了方便理解,并无实际应用。
- ③交换S和SL的颜色。
- ④转至【情况二-情形二】处理,此时原SL结点是新的S结点,原S结点是新的SR结点。
第三种情况:兄弟结点S是红色的
- 情况一:兄弟结点S是父结点P的左子结点
调整方法:以父结点P为支点进行右旋,旋转后,交换父结点P和兄弟结点S的颜色,N的兄弟结点变为黑色,转至【第二种情况】处理。
右旋的流程就不画了,上面已经画了很多次了。
- 情况二:兄弟结点S是父结点P的右子结点
调整方法:以父结点P为支点进行左旋,旋转后,交交换父结点P和兄弟结点S的颜色,N的兄弟结点变为黑色,转至【第二种情况】处理。
至此,红黑树的删除操作也完成了,很复杂,分支特别多。
删除平衡总结
下面总结下。
删除实例
红黑树的删除实例(此实例来源于彻底理解红黑树(三)之 删除)
推荐一个网站:红黑树动画在线演示
可以用来查看红黑树的插入/删除/查找等。
第一步:删除结点50
待删除的结点50既有左子结点,又有右子结点,所以同二叉排序树的删除一样,寻找一个结点来替换待删除结点,一般选择是右子树的最小结点或左子树的最大结点。
如果选择的是左子树的最大结点,那么就是使用结点40交换结点50,结点50没有子结点,可以直接删除结点50。
![]()
同网站测试结果一样
如果选择的是右子树的最小结点,那么就是使用结点60交换结点50,交换后,发现结点50只有一棵右子树,按照二叉排序树的删除规则,直接将右子树的根结点连接在结点50的父结点60上,然后染黑结点70,保证黑色结点的数量,结果如下图:
由于选择不同的结点进行交换,最终导致重新的红黑树不一样。
第二步:删除结点70
注意:只有当删除掉黑色的叶子结点后才会触发红黑树的平衡操作。
该结点没有任何子结点,直接删除。
(这里最开始删除结点70选用的是右子树最小结点60进行交换,所以图是这样的)
但是,注意,刚才删除的结点70是黑色结点,会导致红黑树失衡,必须进行调整,可以看到从根结点到左子树的其他叶子结点的黑色结点个数是3(包含NIL在内),但到右子树的叶子结点的黑色结点个数是2(包含NIL在内),违反了红黑树的第五条性质。
平衡第一步:以结点60为支点右旋,交换结点60和结点20的颜色,详细流程如下:
进行调整后,发现结点N的兄弟结点30是黑色的,所以转至【第二种情况】处理,观察发现兄弟结点30的子结点不全是黑色,同时兄弟结点30是父结点60的左子结点,并且SR结点40是红色,SL结点‘NIL’是黑色,所以符合【第二种情况 - 情况二 - 情形三】。
平衡第二步:以结点30为支点左旋,交换结点30和结点40的颜色,详细流程如下:
进行调整后,需要转至【第二种情况-情况二-情形一】,观察发现也符合,结点N的兄弟结点40是黑色的,结点40的子结点不全是黑色,兄弟结点40是父结点60的左子结点,结点40的SL左子结点30是红色,结点SR是'NIL'黑色的,所以符合,进行调整。
平衡第三步:以结点60为支点右旋,交换结点60和结点40的颜色,染黑结点30,详细流程如下:
到此删除结点70所造成的平衡问题得以解决,总结如下:
第三步:删除结点60
结点60没有子结点,可以直接删除,删除后结点40的右子结点指向NIL
但注意,被删除的结点60是黑色叶子结点,删除后红黑树失衡,从结点20到其他叶子结点的黑色结点个数是3个(包含NIL在内),而到结点40的右子树叶子结点的黑色结点个数只有2个(包含NIL在内),违反了红黑树的第五条性质,所以需要进行调整。
观察发现N结点的兄弟结点30是黑色的,并且结点30的子结点都是黑色,同时结点30的父结点是红色的,符合【第二种情况-情况一-情形二】,进行调整。
平衡第一步:交换结点30和结点40的颜色,平衡完成。
![]()
所以删除结点60的完整过程如下:
第四步:删除结点10
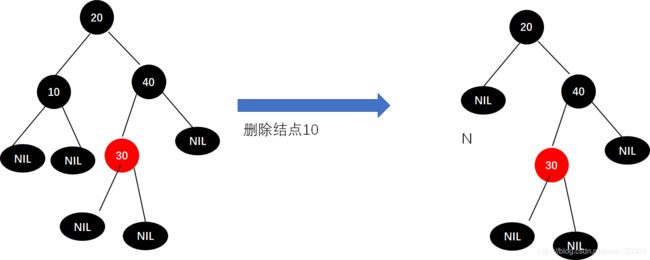
结点10没有子结点,可以直接删除。
但注意,被删除的叶子结点10是黑色的叶子结点,删除后,红黑树就会失衡,因为原来经过结点10的路径的黑色结点个数少了一个,从根结点到其他叶子结点的路径中黑色结点个数是3个(包含NIL在内),但到结点20的左子树路径中黑色结点个数只有2个(包含NIL在内)所以必须进行调整。
观察发现N结点的兄弟结点40是黑色的,但它的子结点不全是黑色的,同时结点40是父结点20的右子结点,结点40的左子结点30是红色的,符合【第二种情况-情况二-情形四】,进行调整。
平衡第一步:以结点40为支点右旋,交换结点40和结点30的颜色,转至【第二种情况-情况二-情形二】
观察发现结点N的兄弟结点30仍然是黑色的,兄弟结点30的子结点不全是黑色的,同时兄弟结点30是父结点20的右子,兄弟结点30的右子结点是红色的,所以按照【第二种情况-情况二-情形二】处理。
平衡第二步:以父结点20为支点左旋,交换结点20和结点30的颜色,染黑结点40,平衡完成
所以删除结点10的完整过程如下:
第五步:删除结点20
结点20没有子结点,直接删除即可。
但注意,结点20是黑色叶子结点,删除后会导致红黑树失衡,需要调整。
观察发现结点N的兄弟结点40是黑色的,并且结点40的子结点都是黑色的,同时结点40的父结点30也是黑色的,按照【第二种情况 - 情况一 - 情形一】处理。
平衡第一步:染红结点40,将父结点30作为新的N结点,递归处理。
删除结点20的完整过程如下:
至此,就已经完成了红黑树删除结点的学习。
注意,无论替换采用的是左子树的最大结点,还是右子树的最小结点,最后删除的结果都是一样,如测试网站最终的结果。
红黑树广泛应用于JDK中,如TreeMap、TreeSet和HashMap,而了解红黑树的目的现阶段就是为了阅读HashMap的源码。
参考链接
- 漫画:什么是红黑树?
- 一文带你彻底读懂红黑树(附详细图解)
- 彻底理解红黑树(二)之 插入
- 彻底理解红黑树(三)之 删除
- 红黑树 - 维基百科