python蒙特卡罗方法

蒙特卡罗模拟

蒙特卡罗（Monte Carlo）方法，又称随机抽样或统计试验方法，是以概率和统计理论方法为基础的一种计算方法
使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。
将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。
 
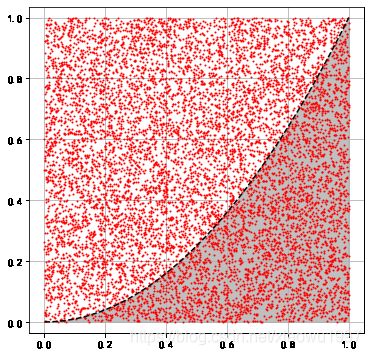
 ① π的计算
 ② 计算积分 y = x**2
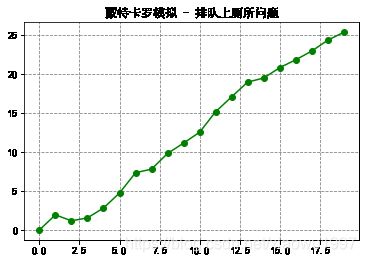
 ③ 排队上厕所问题

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
# π的计算

from matplotlib.patches import Circle

n = 10000
# 投点次数

r = 1.0           # 半径
a, b = (0., 0.)   # 圆心
# 圆的信息

x_min, x_max = a-r, a+r
y_min, y_max = b-r, b+r
# 正方形区域边界

x = np.random.uniform(x_min, x_max, n) # 均匀分布
y = np.random.uniform(y_min, y_max, n)
# 在正方形区域内随机投点
# numpy.random.uniform(low,high,size) → 从一个均匀分布[low,high)中随机采样，均匀分布

d = np.sqrt((x-a)**2 + (y-b)**2)
res = sum(np.where(d < r, 1, 0))
# 计算点到圆心的距离
# 统计落在圆内的点的数目

pi = 4 * res / n
print('pi: ', pi)
# 计算 pi 的近似值 → Monte Carlo方法：用统计值去近似真实值

fig = plt.figure(figsize = (6,6))
axes = fig.add_subplot(1,1,1)
plt.plot(x,y,'ro',markersize = 1)
plt.axis('equal')
# 制图

circle = Circle(xy = (a,b),radius = r, alpha = 0.5 ,color = 'gray')
axes.add_patch(circle)
plt.grid(True, linestyle = "--",linewidth = "0.8")
plt.show()
# 绘制圆形

# 计算积分 y = x**2

n = 10000
# 投点次数

x_min, x_max = 0.0, 1.0
y_min, y_max = 0.0, 1.0   
# 矩形区域边界

x = np.random.uniform(x_min, x_max, n) # 均匀分布
y = np.random.uniform(y_min, y_max, n)
# 在矩形区域内随机投点

def f(x):
    return x**2
# 创建函数 y = x**2

res = sum(np.where(y < f(x), 1, 0))
# 统计 落在函数 y=x^2图像下方的点的数目

integral = res / n
print('integral: ', integral)
# 计算 定积分的近似值

fig = plt.figure(figsize = (6,6)) 
axes = fig.add_subplot(111) 
axes.plot(x, y,'ro',markersize = 1)
plt.axis('equal') 
# 绘制散点图

xi = np.linspace(0,1,100)
yi = xi ** 2
plt.plot(xi,yi,'--k')
plt.fill_between(xi, yi, 0, color ='gray',alpha=0.5,label='area')  
plt.grid()
# 绘制 y = x**2 面积图

# 厕所排队问题
# 1、两场电影结束时间相隔较长，互不影响；
# 2、每场电影结束之后会有20个人想上厕所；
# 3、这20个人会在0到10分钟之内全部到达厕所）；
# 4、每个人上厕所时间在1-3分钟之间
# 首先模拟最简单的情况，也就是厕所只有一个位置，不考虑两人共用的情况则每人必须等上一人出恭完毕方可进行。
# 分析：对于每个人都有如下几个参数：
# 到达时间 / 等待时间 / 开始上厕所时间 / 结束时间

arrivingtime = np.random.uniform(0,10,size = 20)
arrivingtime.sort()
workingtime = np.random.uniform(1,3,size = 20)
# np.random.uniform 随机数：均匀分布的样本值

startingtime = [0 for i in range(20)]
finishtime = [0 for i in range(20)]
waitingtime = [0 for i in range(20)]
emptytime = [0 for i in range(20)]
# 开始时间都是0

print('arrivingtime\n',arrivingtime,'\n')
print('workingtime\n',workingtime,'\n')
print('startingtime\n',startingtime,'\n')
print('finishtime\n',finishtime,'\n')
print('waitingtime\n',waitingtime,'\n')
print('emptytime\n',emptytime,'\n')
print('------')

startingtime[0] = arrivingtime[0]  # 第一个人之前没有人，所以开始时间 = 到达时间
finishtime[0] = startingtime[0] + workingtime[0]   # 第一个人完成时间 = 开始时间 + “工作”时间
waitingtime[0] = startingtime[0]-arrivingtime[0]   # 第一个人不用等待

for i in range(1,len(arrivingtime)):
    if finishtime[i-1] > arrivingtime[i]:
        startingtime[i] = finishtime[i-1]
    else:
        startingtime[i] = arrivingtime[i]
        emptytime[i] = arrivingtime[i] - finishtime[i-1]
    finishtime[i] = startingtime[i] + workingtime[i]
    waitingtime[i] = startingtime[i] - arrivingtime[i]
    print('第%d个人：到达时间 开始时间 “工作”时间 完成时间 等待时间\n' %i,
          arrivingtime[i],
          startingtime[i],
          workingtime[i],
          finishtime[i],
          waitingtime[i],
         '\n')
print('arerage waiting time is %f' %np.mean(waitingtime))
print('------')
# 判断：如果下一个人在上一个人完成之前到达，则 开始时间 = 上一个人完成时间，
# 否则 开始时间 = 到达时间，且存在空闲时间 = 到达时间 - 上一个人完成时间

fig = plt.figure(figsize = (6,4))
plt.plot(waitingtime, '-go')
plt.grid(True,linestyle='--', color = 'gray',linewidth = '0.8')
plt.title('蒙特卡罗模拟 - 排队上厕所问题')
plt.show()
# 图表绘制

arrivingtime
 [0.8372641  1.62596197 3.97249996 4.80112563 4.82940279 5.03125491
 5.04587266 5.75326316 5.87126976 5.90719189 6.16422269 6.25711512
 6.83412713 6.88231082 7.37858062 7.42400951 7.69003956 9.13909226
 9.21176186 9.93258484] 

workingtime
 [2.72102143 1.57999739 1.20784523 1.29215416 2.12428734 2.61389912
 1.1739024  2.12244646 1.36999689 1.64256275 2.7231674  2.4945021
 1.93511629 1.01285069 1.37831419 1.27377539 2.56687652 1.466649
 1.74149452 1.90663883] 

startingtime
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 

finishtime
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 

waitingtime
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 

emptytime
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 

------
第1个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 1.6259619655882962 3.5582855276510745 1.5799973937757374 5.138282921426812 1.9323235620627783 

第2个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 3.972499961728916 5.138282921426812 1.2078452261268569 6.346128147553669 1.1657829596978964 

第3个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 4.801125627345185 6.346128147553669 1.2921541580821607 7.63828230563583 1.5450025202084836 

第4个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 4.829402789889561 7.63828230563583 2.124287341370519 9.762569647006348 2.808879515746269 

第5个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 5.031254911894369 9.762569647006348 2.613899120811082 12.37646876781743 4.7313147351119795 

第6个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 5.045872664765745 12.37646876781743 1.1739024025929237 13.550371170410354 7.330596103051685 

第7个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 5.753263156204841 13.550371170410354 2.1224464616729457 15.6728176320833 7.797108014205514 

第8个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 5.871269755313252 15.6728176320833 1.3699968890088927 17.042814521092193 9.801547876770048 

第9个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 5.907191888954715 17.042814521092193 1.6425627513536287 18.685377272445823 11.135622632137478 

第10个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 6.164222691015427 18.685377272445823 2.723167404176716 21.40854467662254 12.521154581430396 

第11个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 6.257115119493369 21.40854467662254 2.4945020988427484 23.903046775465288 15.151429557129171 

第12个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 6.834127129713599 23.903046775465288 1.9351162905151953 25.838163065980485 17.06891964575169 

第13个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 6.882310817558359 25.838163065980485 1.012850688047494 26.851013754027978 18.955852248422126 

第14个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 7.378580616086149 26.851013754027978 1.3783141911474743 28.229327945175452 19.472433137941827 

第15个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 7.424009512966082 28.229327945175452 1.2737753934037266 29.50310333857918 20.80531843220937 

第16个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 7.690039556589346 29.50310333857918 2.566876524132043 32.06997986271122 21.813063781989833 

第17个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 9.139092261599878 32.06997986271122 1.4666489998661398 33.53662886257736 22.930887601111344 

第18个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 9.211761857787128 33.53662886257736 1.7414945191579325 35.27812338173529 24.32486700479023 

第19个人：到达时间 开始时间 “工作”时间 完成时间 等待时间
 9.932584835977467 35.27812338173529 1.9066388335278996 37.18476221526319 25.345538545757826 

arerage waiting time is 12.331882