《TensorFlow 深度学习》阅读笔记（四）——卷积神经网络

三、卷积神经网络

---

1. 前述

   • 局部相关性

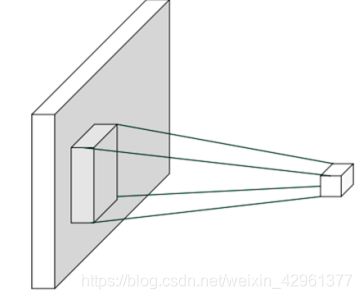
     我们以 2D 图片数据为例，如果简单地认为与当前像素欧式距离(Euclidean distance)小于和等于$\frac{k}{\sqrt{2}}$的像素点重要性较高，欧式距离大于$\frac{k}{\sqrt{2}}$到像素点重要性较低，那么我们就很轻松的简化了每个像素点的重要性分布问题，以实心网络所在的像素为参考，它周边欧式距离小于和等于$\frac{k}{\sqrt{2}}$的像素点以矩形网格表示，网格内的像素点重要性较高，网格外的像素点较低。这个高宽为$\frac{k}{\sqrt{2}}$的窗口称为感受野(receptive field)，它表征了每个像素对于中心像素的重要性分布情况，网格内的像素才会被考虑，网格外的像素对于中心像素会被简单地忽略。

     利用局部相关性的思想，我们把感受野窗口的高、宽记为 k(感受野的高、宽可以不相等，为了便与表达，我们只讨论高宽相等的情况)，当前位置的节点与大小为 k 的窗口内的所有像素相连接，与窗口外的其他像素点无关。如下图：

     

   • 权值共享

     即使用一个卷积核对，通过上下左右滑动，对整张图片的像素值所包含的信息进行提取。利用权值共享的思想，可以有效的降低网络的超参数数量。

2. 卷积运算

   在信号处理领域，1D 连续信号的卷积运算被定义 2 个函数的积分：函数()，函数()，其中()经过了翻转(−)和平移后变成( − )。卷积的“卷”是指翻转平移操作，“积”是指积分运算，1D 连续卷积定义为：
   $$(f\ast g)(n)={\int }_{-\infty }^{\infty }f(\tau )g(n-\tau )d\tau$$
   离散卷积将积分变成累加运算：
   $$(f\ast g)(n)=\sum _{\tau =-\infty }^{\infty }f(\tau )g(n-\tau )$$
   在计算机视觉中，卷积运算基于 2D 图片函数(, )和 2D 卷积核(, )，其中(, )和(, )仅在各自窗口有效区域存在值，其他区域视为 0，其定义为：
   $$[f\ast g](m,n)=\sum _{i=-\infty }^{\infty }\sum _{i=-\infty }^{\infty }f(i,j)g(m-i,n-j)$$
   其中m，n控制这卷积核的位置。

   • 卷积运算流程

     2D 离散卷积运算流程：每次通过移动卷积核窗口与图片对应位置处的像素相乘累加，得到此位置的输出值。

     卷积核即是窗口为k 大小的权值矩阵 W，对应到图上大小为 k 的窗口，即为感受野，感受野与权值矩阵 W 相乘累加，得到此位置的输出值。通过权值共享，我们从左上方逐步向左、向下移动卷积核，提取每个位置上的像素特征，直至最右下方，完成卷积运算。

3. 卷积层

   以 2D 图片数据为例，卷积层接受高、宽分别为h, w，通道数为$c_{in}$的输入特征图x，在$c_{out}$个高、宽都为k，通道数为$c_{in}$的卷积核作用下，生成高、宽分别为h’, w’，通道数为$c_{out}$的特征图输出。需要注意的是，卷积核的高宽可以不等。

   • 单通道输入，单卷积核

     单通道输入$c_{in}=1$，如灰度图片只有灰度值一个通道，单个卷积核$c_{out}=1$ 的情况。此时根据卷积运算的流程可以简单的计算。

   • 多通道输入，单卷积核(一个多通道的卷积核)

     在多通道输入的情况下，卷积核的通道数需要和输入 X 的通道数量相匹配，卷积核的第 i 个通道和 X 的第 i 个通道相运算，得到第 i 个中间矩阵，此时可以视为单通道输入与单卷积核的情况，所有通道的中间矩阵对应元素再次相加，作为最终输出。

     一般来说，一个固定的卷积核只能完成某种逻辑的特征提取，当需要同时提取多种逻辑特征时，可以通过增加多个卷积核来得到多种特征，提高神经网络的表达能力，这就是多通道输入，多卷积核的情况。

   • 多通道输入，多卷积核(多个多通道的卷积核)

     第 i 个卷积核与输入进行多通道，单卷积核情况下的运算，得到一个输出矩阵，此矩阵作为多通道多卷积核情况下的输出的第 i 通道。即此情况下的输出，有多少个卷积核，输出的张量就有多少个通道。

   步长，指感受野窗口每次移动的长度单位，对于 2D 输入来说，分为沿 x 方向和 y 方向的移动长度。通过设定步长 s，可以有效的控制信息密度的提取。当步长设计的较小时，感受野以较小幅度移动窗口，有利于提取到更多的特征信息，输出张量的尺寸也更大；当步长设计的较大时，感受野以较大幅度移动窗口，有利于减少计算代价，过滤冗余信息，输出张量的尺寸也更小。

   经过卷积运算后的输出O的高宽一般会小于输入X的高宽，即使是步长s = 1 时，输出O的高宽也会略小于输入高宽。其计算公式如下：
   $$h^{\prime }=h-k+1$$
   其中，h为输入X的高或者宽，k为卷积核的高或者宽。

   若想保持输出的大小与输入的大小相同，可以在输入的周围填充合适层数，填充数值一般默认为0。卷积神经层的输出尺寸[b,h’,w’,$c_{out}$] 由卷积核的数量$c_{out}$，卷积核的大小 k，步长 s，填充数 p(只考虑上下填充数量$p_h$相同，左右填充数量$p_w$相同的情况)以及输入X的高宽 h/w共同决定，他们之间的数学关系可以表达为：
   $$h^{\prime }=\lfloor \frac{h+2\ast p_h-k}{s}\rfloor +1$$
   w’的计算与上式一致。

   在 TensorFlow 中，在s = 1时，如果希望输出 O 和输入 X 高、宽相等，只需要简单地设置参数 padding=”SAME”即可使 TensorFlow 自动计算 padding 数量。

4. 卷积层的实现

   • 自定义权值

     通过 tf.nn.conv2d 函数可以方便地实现 2D 卷积运算。tf.nn.conv2d基于输入 X: [b, h, w, $c_{in}$] 和卷积核 W: [k, k, $c_{in}$, $c_{out}$] 进行卷积运算，得到输出O: [b, h’, w’, $c_{out}$] ，其中$c_{in}$表示输入通道数，$c_{out}$表示卷积核的数量，也是输出特征图的通道数。如下：

     # 步长为 1, padding为0,padding=[[0,0],[上,下],[左,右],[0,0]]
     out = tf.nn.conv2d(x,w,strides=1,padding=[[0,0],[0,0],[0,0],[0,0]])
     
     # 步长为 1, padding 为 1,
     out = tf.nn.conv2d(x,w,strides=1,padding=[[0,0],[1,1],[1,1],[0,0]])
     
     # 步长为,padding 设置为输出、输入同大小
     # 需要注意的是, padding=same 只有在 strides=1 时才是同大小
     #当 > 时，设置 padding='SAME'将使得输出高、宽将成1/倍地减少
     out = tf.nn.conv2d(x,w,strides=1,padding='SAME')
     

   • 卷积层类

     使用类方式会(在创建类时或build 时)自动创建需要的权值张量和偏置向量，用户不需要记忆卷积核张量的定义格式，因此使用起来更简单方便，但是灵活性也较低。在新建卷积层类时，只需要指定卷积核数量参数 filters，卷积核大小 kernel_size，步长strides，填充padding 等即可，如:

     #创建了 4 个 3x3 大小的卷积核的卷积层，步长为 1，padding 方案为'SAME'
     layer = layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME')
     

     如果卷积核高宽不等，步长行列方向不等，此时需要将 kernel_size 参数设计为($k_h$, $k_w$)，strides 参数设计为($s_h$, $s_w$)。如下：

     #创建4个3x4大小的卷积核，竖直方向移动步长2，水平方向移动步长1
     layer = layers.Conv2D(4,kernel_size=(3,4),strides=(2,1),padding='SAME')
     

     类 Conv2D 中，保存了卷积核张量 W 和偏置 b，可以通过类成员trainable_variables直接返回 W，b 的列表。

5. 池化层

   除了通过设置步长，还有一种专门的网络层可以实现尺寸缩减功能，那就是池化层(Pooling layer)。池化层同样基于局部相关性的思想，通过从局部相关的一组元素中进行采样或信息聚合，从而得到新的元素值。特别地，最大池化层(Max Pooling)从局部相关元素集中选取最大的一个元素值，平均池化层(Average Pooling)从局部相关元素集中计算平均值并返回。其池化核的感受野无权值，通过下式进行取值：
   $$x^{\prime }=\max (x\in \{输入X中被感受野盖住的值\})$$
   输入X在经过池化层之后的长或宽用下式进行计算：
   $$h^{\prime }=\lfloor \frac{h-k}{s}\rfloor +1$$
   其中，h为原来的长或宽，k为感受野长或宽，s为步长。常用的k=2，s=2池化层，将输入X按照上述取值原则将长或宽缩放为原来的一半，以达到降维的目的。

6. 池化层的实现

   通过layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same')可以创建最大池化层，此时实现宽高减半的操作。

7. BatchNorm 层(BN层)

   Batch Nomalization(简写为 BatchNorm，或 BN)层 。BN 层的提出，使得网络的超参数的设定更加自由，比如更大的学习率，更随意的网络初始化等，同时网络的收敛速度更快，性能也更好。通过堆叠 Conv-BN-ReLU-Pooling 方式往往可以获得不错的模型性能。

   神经网络在反向传播时，可能会因为得到的导数很小而导致梯度弥散。此时可以考虑将输入标准化映射到0附近的一个小的区间，从而使得网络层的输入X的分布相近，以便优化时能够收敛得更快。数据标准化操作可以达到这样的目的：
   $$\hat{x}=\frac{x-{\mu }_r}{\sqrt{{\sigma }_r^2+ϵ}}$$
   其中，${\mu }_r,{\sigma }_r^2$为所有数据的统计均值及方差，$ϵ$为防止出现分母为零而设置的一个较小的数。

   在基于 Batch 的训练阶段，考虑Batch 内部的均值${\mu }_B$和方差${\sigma }_B^2$:
   $$\begin{gathered} {\mu }_B=\frac{1}{m}\sum _{i=1}^m{x}_i \\ {\sigma }_B^2=\frac{1}{m}\sum _{i=1}^m(x_i-{\mu }_B{)}^2 \end{gathered}$$
   根据根据统计原理，可以近似看作${\mu }_r,{\sigma }_r^2$，其中m为Batch的样本数，则在训练阶段可以通过：
   $${\hat{x}}_{train}=\frac{x_{train}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$
   将输入标准化。

   在测试阶段，根据记录的每个 Batch 的${\mu }_B,{\sigma }_B^2$估计出所有训练数据的${\mu }_r,{\sigma }_r^2$，通过：
   $${\hat{x}}_{test}=\frac{x_{test}-{\mu }_r}{\sqrt{{\sigma }_r^2+ϵ}}$$
   将测试阶段的每层数据的输入标准化。

   为了提高 BN 层的表达能力，BN 层作者引入了“scale and shift”技巧，将$\hat{x}$变量再次映射变换：
   $$\dot{x}=\hat{x}\ast \gamma +\beta$$
   其中$\gamma$参数实现对标准化后的$\hat{x}$再次进行缩放，$\beta$参数实现对标准化的̂进行平移，不同的是，$\gamma ,\beta$参数均由反向传播算法自动优化，实现网络层“按需”缩放平移数据的分布的目的。

   • 前向传播

     训练阶段：首先计算出${\mu }_B,{\sigma }_B^2$，然后根据：
     $${\dot{x}}_{train}={\hat{x}}_{train}\ast \gamma +\beta$$
     计算BN层输出。同时通过：
     $$\begin{gathered} {\mu }_r=momentum\ast {\mu }_r+(1-momentum)\ast {\mu }_B \\ {\sigma }_r^2=momentum\ast {\sigma }_r^2+(1-momentum){\sigma }_B^2 \end{gathered}$$
     对${\mu }_r,{\sigma }_r^2$进行更新。

     测试阶段：BN层根据：
     $${\dot{x}}_{test}={\hat{x}}_{test}\ast \gamma +\beta$$
     计算BN层输出。用到的参数由前向传播得来。

   • 反向更新

     训练时，根据梯度更新法则对参数$\gamma ,\beta$进行优化。需要注意的是，对于输入 X: [b,h,w,c]，BN 层并不是计算每个点的${\mu }_B,{\sigma }_B^2$，而是在通道轴 c上面统计每个通道上面所有数据的${\mu }_B,{\sigma }_B^2$，因此${\mu }_B,{\sigma }_B^2$是每个通道上所有其他维度的均值和方差。数据有 c 个通道数，则有 c 个均值产生。

8. BN层的实现

   通过 layers.BatchNormalization()类可以非常方便地实现 BN 层：

   layer=layers.BatchNormalization()
   

   与全连接层、卷积层不同，BN 层的训练阶段和测试阶段的行为不同，需要通过设置神经网络模型类对象的training标志位来区分训练模式还是测试模式：

   out = model(x, training=True) #设置为训练模式
   out = model(x, training=False) #设置为测试模式
   

9. 卷积层的变种

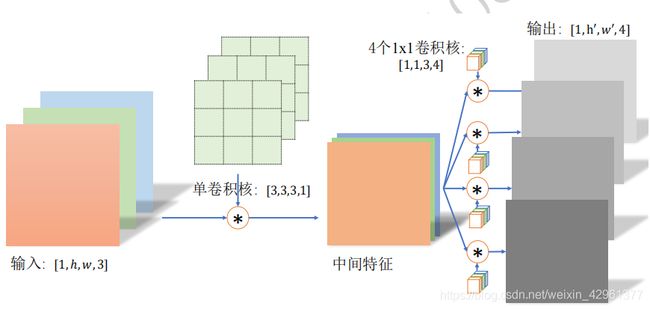
   • 分离卷积：分离卷积的计算流程与普通多通道单核卷积运算不同，卷积核的每个通道与输入的每个通道进行卷积运算，得到多个通道的中间特征。这个多通道的中间特征张量接下来进行多个1x1 卷集核的普通卷积运算，得到多个高宽不变的输出，这些输出在通道轴上面进行拼接，从而产生最终的分离卷积层的输出。如下图：

     

   • 空洞卷积：空洞卷积在不增加网络参数的条件下，提供了更大的感受野窗口。但是在使用空洞卷积设置网络模型时，需要精心设计 dilation rate 参数来避免出现网格效应，当其值为2时，表示每两个采样点采一次样，即中间间隔为1，以此类推。较大的dilation rate 参数并不利于小物体的检测、语义分割等任务。如下：

     # 空洞卷积，1 个 3x3 的卷积核
     layer = layers.Conv2D(1,kernel_size=3,strides=1,dilation_rate=2)
     

   1. 转置卷积:通过在输入之间填充大量的 padding 来实现输出高宽大于输入高宽的效果，从而实现向上采样的目的。设输入的宽高相同，即h=w。

      矩阵角度理解：转置卷积的转置是指卷积核矩阵 W 产生的稀疏矩阵W′在计算过程中需要转置$W^T$，再进行矩阵相乘运算，而普通卷积并没有转置W′的步骤。这也是它被称为转置卷积的名字由来。

      此时，卷积核矩阵通过在周围填充0至与输入矩阵相同大小，卷积核的矩阵位置应当使得填充后与输入重叠时，与普通卷积操作时，卷积核所框住的数据相对应。然后将所有情况下的填充后的卷积核拉长，形成一个新的与输入矩阵拉长后列数相等，行数与进行的卷积次数相等的矩阵。那么普通卷积可以表达为输入矩阵拉长后与卷积核变换之后的矩阵相乘的结果。转置卷积阶段则是要通过卷积核变换后的矩阵与普通卷积的输出做矩阵运算，最终得到与输入矩阵大小相同的一个矩阵。如下：
      $$\begin{gathered} X\ast W=O \\ {X}^{\prime }W\ast W^T=O\ast W^T \end{gathered}$$
      需要注意的是，W矩阵一般不是可逆矩阵，所以得到的X’ 与 原输入X并不相等。

      实现：通过tf.nn.conv2d_transpose(out,w,strides,padding,output_shape)其中，out为普通转置卷积的输出，w为卷积核，输入步长普通卷积的卷积核的步长，padding与普通卷积相同，同时指定输出形状。如：

      # 普通卷积的输出作为转置卷积的输入，进行转置卷积运算
      xx = tf.nn.conv2d_transpose(out,w,strides=2,padding='VALID',output_shape=[1,5,5,1])
      

   • 深度残差网络：在较深层数的神经网络中间，梯度信息由网络的末层逐层传向网络的首层时，传递的过程中会出现梯度接近于 0的现象。网络层数越深，梯度弥散现象可能会越严重。此时，通过在输入和输出之间添加一条直接连接的 Skip Connection 可以让神经网络具有回退的能力。通过这种方式网络模型可以自动选择是否经由这两个卷积层完成特征变换，还是直接跳过这两个卷积层而选择 Skip Connection，亦或结合两个卷积层和 Skip Connection 的输出。

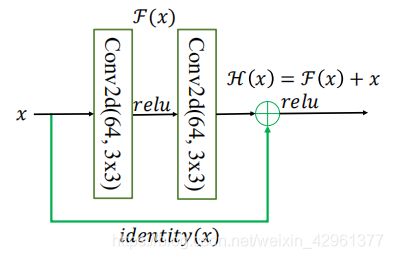
     原理：输入x通过两个卷积层，得到特征变换后的输出F(x)，与输入x进行对应元素的相加运算，得到最终输出。

     H(x)叫做残差模块(Residual Block，ResBlock)。由于被 Skip Connection 包围的卷积神经网络需要学习映射F(x) = H(x) − x，故称为残差网络。如下图：

     

     为了能够满足输入与卷积层的输出F(x)能够相加运算，需要输入的 shape 与F(x)的shape 完全一致。当出现 shape 不一致时，一般通过在 Skip Connection 上添加额外的卷积运算环节将输入x变换到与F(x)相同的shape，其中identity()以 1x1 的卷积运算居多，主要用于调整输入的通道数。

     实现：首先创建一个新类，在初始化阶段创建残差块中需要的卷积层，激活函数层等，首先新建F(X)卷积层：

     class BasicBlock(layers.Layer):
       	# 残差模块类
        	def __init__(self, filter_num, stride=1):
             super(BasicBlock, self).__init__()
          	# f(x)包含了 2 个普通卷积层，创建卷积层 1
       		self.conv1 = layers.Conv2D(filter_num, (3, 3), strides=stride, padding='same')
          	self.bn1 = layers.BatchNormalization()
       		self.relu = layers.Activation('relu')
          	# 创建卷积层 2
       		self.conv2 = layers.Conv2D(filter_num, (3, 3), strides=1, padding='same')
          	self.bn2 = layers.BatchNormalization()
             #当F(x)的形状与x不同时，无法直接相加,新建identity(x)卷积层，来完成的形状转换
             if stride != 1: # 插入 identity 层
          		self.downsample = Sequential()
       			self.downsample.add(layers.Conv2D(filter_num, (1, 1), strides=stride))
          	else: # 否则，直接连接
       			self.downsample = lambda x:x
                      
           #在前向传播时，只需要将F(x)与identity(x)相加，并添加 ReLU 激活函数即可
        	def call(self, inputs, training=None):
          	# 前向传播函数
          	out = self.conv1(inputs) # 通过第一个卷积层
          	out = self.bn1(out)
          	out = self.relu(out)
       		out = self.conv2(out) # 通过第二个卷积层
          	out = self.bn2(out)
       		# 输入通过 identity()转换
          	identity = self.downsample(inputs)
       		# f(x)+x 运算
          	output = layers.add([out, identity])
          	# 再通过激活函数并返回
       		output = tf.nn.relu(output)
          	return output
     

10. 手写字MNIST数据集实战

    源码：

    import tensorflow as tf
    from tensorflow import keras
    from tensorflow.keras import layers, optimizers, Sequential, losses, datasets
    
    BATCH = 64
    TEMPLATE = 'train_losse: {:.4f}, train_accuracy: {:.4f}, test_losse: {:.4f}, test_accuracy: {:.4f}'
    
    (x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
    x_train = x_train / 255.0
    x_test = x_test / 255.0
    x_train = tf.expand_dims(x_train, axis=3)
    x_test = tf.expand_dims(x_test, axis=3)
    datatrain = tf.data.Dataset.from_tensor_slices((x_train, y_train))
    datatrain = datatrain.shuffle(10000).batch(BATCH)
    data_test = tf.data.Dataset.from_tensor_slices((x_test,y_test))
    data_test = data_test.shuffle(5000).batch(BATCH)
    
    model = Sequential([
        layers.Conv2D(6, kernel_size=3, strides=1),
        layers.MaxPooling2D(pool_size=2, strides=2),
        layers.ReLU(),
        layers.Conv2D(16, kernel_size=3,strides=1),
        layers.MaxPooling2D(pool_size=2,strides=2),
        layers.ReLU(),
        layers.Flatten(),
    
        layers.Dense(120, activation='relu'),
        layers.Dense(84, activation='relu'),
        layers.Dense(10)])
    
    criteon = losses.CategoricalCrossentropy(from_logits=True)
    optimizer = optimizers.Adam()
    losse_train = keras.metrics.Mean(name='losse_train')
    acc_train = keras.metrics.SparseCategoricalAccuracy(name='acc_train')
    losse_test = keras.metrics.Mean(name='losse_test')
    acc_test = keras.metrics.SparseCategoricalAccuracy(name='acc_test')
    
    for epoche in range(5):
        losse_train.reset_states()
        acc_train.reset_states()
        for step, (x,y) in enumerate(datatrain):
            with tf.GradientTape() as tape:
                out = model(x)
                y_onehot = tf.one_hot(y, depth=10)
                losse = criteon(y_onehot, out)
            grads = tape.gradient(losse, model.trainable_variables)
            optimizer.apply_gradients(zip(grads, model.trainable_variables))
            
            losse_train(losse)
            acc_train(y, out)
            
        for step_t, (x_t,y_t) in enumerate(data_test):
            out_t = model(x_t)
            yonehot = tf.one_hot(y_t, depth=10)
            losse_t = criteon(yonehot, out_t)
            
            losse_test(losse_t)
            acc_test(y_t, out_t)
        
        print(TEMPLATE.format(losse_train.result(),acc_train.result(),losse_test.result(), acc_test.result()))
    
    

    结果：

    train_losse: 0.2255, train_accuracy: 0.9332, test_losse: 0.0916, test_accuracy: 0.9686
    train_losse: 0.0742, train_accuracy: 0.9775, test_losse: 0.0770, test_accuracy: 0.9745
    train_losse: 0.0546, train_accuracy: 0.9832, test_losse: 0.0689, test_accuracy: 0.9774
    train_losse: 0.0421, train_accuracy: 0.9865, test_losse: 0.0643, test_accuracy: 0.9789
    train_losse: 0.0338, train_accuracy: 0.9893, test_losse: 0.0602, test_accuracy: 0.9804