投资组合理论在python中的应用
Tushare+Python验证投资组合理论
一、数据来源——Tushare
Tushare大数据开放社区免费提供各类金融数据。数据丰富:拥有丰富的数据内容,如股票、基金、期货、数字货币等行情数据,公司财务、基金经理等基本面数据;获取简单:SDK开发包支持语言,同时提供HTTP Restful接口,最大程度方便不同人群的使用;落地方便:提供多种数据储存方式,如Oracle、MySQL,MongoDB、HDF5、CSV等,为数据获取提供了性能保证。
二、理论知识——投资组合理论
三、成果展示
1、简要说明3只股票的选股理由,以及股价指数的选择理由。
无风险利率(年):1.50%
随机选择两只股票:600689上海三毛,600690海尔智家
自选三只股票:002019亿帆医药,601928凤凰传媒,300059东方财富
三只股票的选股理由
宏观:疫情过后,国家对于医药行业给予大力支持,亿帆医药作为医药领域的创新代表,潜力非常巨大;疫情也促使在线教育蓬勃发展,凤凰传媒持有大量现金并投资了一部分在线教育企业,且其自身业绩一直很好;东方财富属于互联网金融行业,其经营范围广泛且未来成长性较高。
微观:在东方财富上察看几只股票的研报可知,他们都是财务状况、经营状况良好且成长性高的企业。
from prettytable import PrettyTable
x= PrettyTable(["股票代码", "600689", "600690","002019","601928","300059"])
x.add_row(["证券简称","上海三毛","海尔智家","亿帆医药","凤凰传媒","东方财富"])
print(x)+----------+----------+----------+----------+----------+----------+
| 股票代码 | 600689 | 600690 | 002019 | 601928 | 300059 |
+----------+----------+----------+----------+----------+----------+
| 证券简称 | 上海三毛 | 海尔智家 | 亿帆医药 | 凤凰传媒 | 东方财富 |
+----------+----------+----------+----------+----------+----------+
股价指数:000300沪深300指数
选择理由:沪深300指数样本覆盖了沪深市场六成左右的市值,具有良好的市场代表性,有利于投资者全面把握市场运行状况,并能够作为投资业绩的评价标准,为指数化投资和指数衍生产品创新提供了基础条件。
2、确定并画出风险资产的有效边界,标出市场组合与等权重组合。
import tushare as ts
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=Falsecons = ts.get_apis()
SH=ts.bar('600689', conn=cons, freq='D', start_date='2018-01-01',end_date='2020-01-01')#选取上海三毛2018-2020的数据,以“SH”缩写代表该股票
SH本接口即将停止更新,请尽快使用Pro版接口:https://tushare.pro/document/2
| code | open | close | high | low | vol | amount | p_change | |
|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||
| 2019-12-31 | 600689 | 9.64 | 9.80 | 9.97 | 9.63 | 38844.0 | 38199836.0 | 1.45 |
| 2019-12-30 | 600689 | 9.52 | 9.66 | 9.68 | 9.41 | 17645.0 | 16899208.0 | 0.94 |
| 2019-12-27 | 600689 | 9.68 | 9.57 | 9.68 | 9.56 | 12860.0 | 12367035.0 | -0.42 |
| 2019-12-26 | 600689 | 9.56 | 9.61 | 9.65 | 9.55 | 10453.0 | 10036308.0 | 0.73 |
| 2019-12-25 | 600689 | 9.52 | 9.54 | 9.63 | 9.48 | 12995.0 | 12426958.0 | 0.21 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2018-01-08 | 600689 | 11.85 | 11.91 | 12.05 | 11.78 | 22161.0 | 26282188.0 | -0.58 |
| 2018-01-05 | 600689 | 12.08 | 11.98 | 12.22 | 11.90 | 37137.0 | 44709436.0 | -2.92 |
| 2018-01-04 | 600689 | 11.65 | 12.34 | 12.60 | 11.58 | 42366.0 | 50809752.0 | 5.56 |
| 2018-01-03 | 600689 | 11.50 | 11.69 | 11.72 | 11.43 | 29147.0 | 33809136.0 | 1.39 |
| 2018-01-02 | 600689 | 11.43 | 11.53 | 11.58 | 11.32 | 21487.0 | 24647386.0 | NaN |
485 rows × 8 columns
HE=ts.bar('600690', conn=cons, freq='D', start_date='2018-01-01',end_date='2020-01-01')#选取海尔智家2018-2020的数据
YF=ts.bar('002019 ', conn=cons, freq='D', start_date='2018-01-01',end_date='2020-01-01')#选取亿帆医药2018-2020的数据
FH=ts.bar('601928', conn=cons, freq='D', start_date='2018-01-01',end_date='2020-01-01')#选取凤凰传媒2018-2020的数据
DF=ts.bar('300059', conn=cons, freq='D', start_date='2018-01-01',end_date='2020-01-01')#选取东方财富2018-2020的数据
HS = ts.bar('000300', conn=cons, asset='INDEX', start_date='2018-01-01',end_date='2020-01-01')#选取沪深300指数2018-2020的数据本接口即将停止更新,请尽快使用Pro版接口:https://tushare.pro/document/2
本接口即将停止更新,请尽快使用Pro版接口:https://tushare.pro/document/2
本接口即将停止更新,请尽快使用Pro版接口:https://tushare.pro/document/2
本接口即将停止更新,请尽快使用Pro版接口:https://tushare.pro/document/2
本接口即将停止更新,请尽快使用Pro版接口:https://tushare.pro/document/2
SH=SH.rename(columns={
'close':'上海三毛'})
HE=HE.rename(columns={
'close':'海尔智家'})
YF=YF.rename(columns={
'close':'亿帆医药'})
FH=FH.rename(columns={
'close':'凤凰传媒'})
DF=DF.rename(columns={
'close':'东方财富'})
HS=HS.rename(columns={
'close':'沪深300'})market=HS['沪深300'].to_frame()R_HS300=np.log(market/market.shift(1)) #按照对数收益率的计算公式得到市场收益率
R_HS300=R_HS300.dropna() #删除缺省的数据
Rm=R_HS300.mean()*252 #计算市场组合的年化平均收益率
Vm=R_HS300.std()*np.sqrt(252) #计算市场组合的年化波动率
print('市场组合的收益率',round(Rm,4))
print('市场组合的波动率',round(Vm,4))市场组合的收益率 沪深300 -0.0012
dtype: float64
市场组合的波动率 沪深300 0.2073
dtype: float64
data=pd.concat([SH['上海三毛'],HE['海尔智家'],YF['亿帆医药'],FH['凤凰传媒'],DF['东方财富']],axis=1)
data.head() #查看前5行数据| 上海三毛 | 海尔智家 | 亿帆医药 | 凤凰传媒 | 东方财富 | |
|---|---|---|---|---|---|
| datetime | |||||
| 2018-01-02 | 11.53 | 18.99 | 22.92 | 8.17 | 13.00 |
| 2018-01-03 | 11.69 | 18.73 | 22.75 | 8.21 | 13.24 |
| 2018-01-04 | 12.34 | 19.04 | 22.85 | 8.20 | 13.05 |
| 2018-01-05 | 11.98 | 18.98 | 22.40 | 8.20 | 13.06 |
| 2018-01-08 | 11.91 | 19.83 | 21.84 | 8.19 | 13.20 |
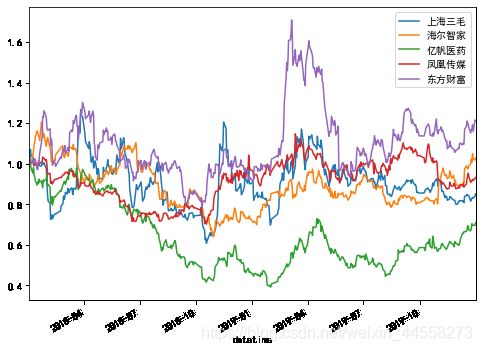
(data/data.iloc[0]).plot(figsize=(8,6)) #将股价按首个交易日进行归一处理并可视化
R=np.log(data/data.shift(1)) #按照对数收益率的计算公式得到股票收益率
R=R.dropna() #删除缺省的数据
R.describe
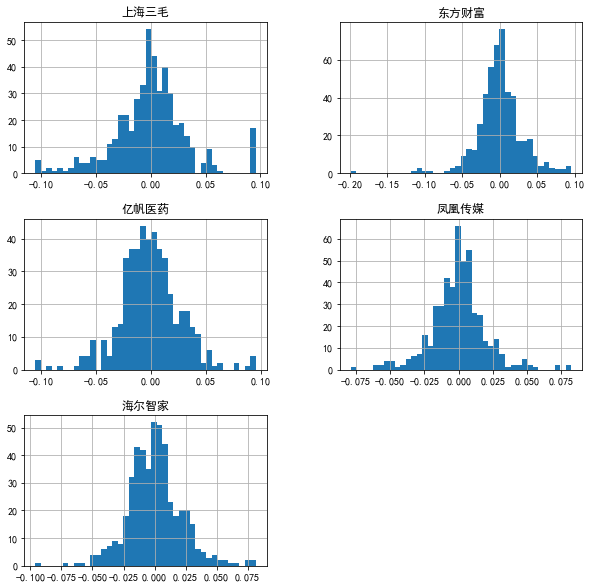
R.hist(bins=40,figsize=(10,10)) #以直方图形式可视化股票收益率C:\ProgramData\Anaconda3\lib\site-packages\pandas\plotting\_matplotlib\tools.py:307: MatplotlibDeprecationWarning:
The rowNum attribute was deprecated in Matplotlib 3.2 and will be removed two minor releases later. Use ax.get_subplotspec().rowspan.start instead.
layout[ax.rowNum, ax.colNum] = ax.get_visible()
C:\ProgramData\Anaconda3\lib\site-packages\pandas\plotting\_matplotlib\tools.py:307: MatplotlibDeprecationWarning:
The colNum attribute was deprecated in Matplotlib 3.2 and will be removed two minor releases later. Use ax.get_subplotspec().colspan.start instead.
layout[ax.rowNum, ax.colNum] = ax.get_visible()
C:\ProgramData\Anaconda3\lib\site-packages\pandas\plotting\_matplotlib\tools.py:313: MatplotlibDeprecationWarning:
The rowNum attribute was deprecated in Matplotlib 3.2 and will be removed two minor releases later. Use ax.get_subplotspec().rowspan.start instead.
if not layout[ax.rowNum + 1, ax.colNum]:
C:\ProgramData\Anaconda3\lib\site-packages\pandas\plotting\_matplotlib\tools.py:313: MatplotlibDeprecationWarning:
The colNum attribute was deprecated in Matplotlib 3.2 and will be removed two minor releases later. Use ax.get_subplotspec().colspan.start instead.
if not layout[ax.rowNum + 1, ax.colNum]:
array([[,
],
[,
],
[,
]],
dtype=object)
R_mean=R.mean()*252 #计算股票的年化平均收益率
print(R_mean)上海三毛 -0.070693
海尔智家 0.028426
亿帆医药 -0.201691
凤凰传媒 -0.035634
东方财富 0.082592
dtype: float64
R_cov=R.cov()*252 #计算股票的协方差矩阵并且年化处理
print(R_cov) 上海三毛 海尔智家 亿帆医药 凤凰传媒 东方财富
上海三毛 0.290920 0.041898 0.077502 0.057104 0.071736
海尔智家 0.041898 0.120252 0.051979 0.027413 0.065728
亿帆医药 0.077502 0.051979 0.195627 0.058504 0.095002
凤凰传媒 0.057104 0.027413 0.058504 0.099974 0.066682
东方财富 0.071736 0.065728 0.095002 0.066682 0.230380
R_corr=R.corr() #计算股票的相关系数矩阵
print(R_corr) 上海三毛 海尔智家 亿帆医药 凤凰传媒 东方财富
上海三毛 1.000000 0.224009 0.324870 0.334837 0.277095
海尔智家 0.224009 1.000000 0.338900 0.250014 0.394898
亿帆医药 0.324870 0.338900 1.000000 0.418335 0.447505
凤凰传媒 0.334837 0.250014 0.418335 1.000000 0.439384
东方财富 0.277095 0.394898 0.447505 0.439384 1.000000
R_vol=R.std()*np.sqrt(252) #计算股票收益率的年化波动率
print(R_vol)上海三毛 0.539370
海尔智家 0.346774
亿帆医药 0.442297
凤凰传媒 0.316187
东方财富 0.479979
dtype: float64
分析:由相关系数矩阵看出五只股票之间的相关性较高,投资组合的分散化效果较弱
Rp_list=[] #建立一个初始的投资组合收益率数列
Vp_list=[] #建立一个初始的投资组合收益波动率数列
for i in np.arange(1000): #生成1000个不同权重的预期收益率与收益波动率
x=np.random.random(5)
weights=x/sum(x)
Rp_list.append(np.sum(weights*R_mean))
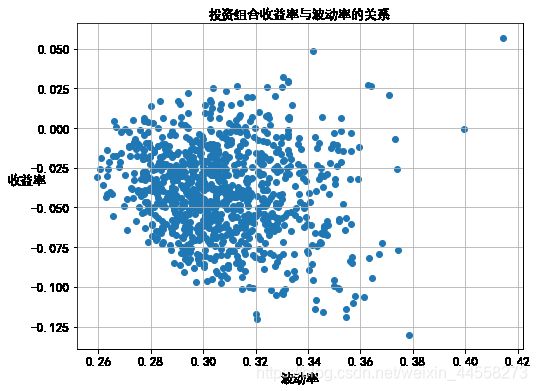
Vp_list.append(np.sqrt(np.dot(weights,np.dot(R_cov,weights.T))))plt.figure(figsize=(8,6))
plt.scatter(Vp_list,Rp_list)
plt.xlabel(u'波动率',fontsize=13)
plt.ylabel(u'收益率',fontsize=13,rotation=0)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.title(u'投资组合收益率与波动率的关系',fontsize=13)
plt.grid('True')
plt.show() #画出可行集weights=np.array([0.2,0.2,0.2,0.2,0.2])
R_port=np.sum(weights*R_mean)
vol_port=np.sqrt(np.dot(weights,np.dot(R_cov,weights.T)))
print('等权重投资组合的预期收益率:',round(R_port,4))
print('等权重投资组合收益波动率:',round(vol_port,4))等权重投资组合的预期收益率: -0.0394
等权重投资组合收益波动率: 0.2942
import scipy.optimize as sco #导入Scipy的子模块optimizedef f(w): #定义一个需要求解最优化的函数
w=np.array(w) #设置投资组合中每只股票的权重
Rp_opt=np.sum(w*R_mean) #计算最优投资组合的预期收益率
Vp_opt=np.sqrt(np.dot(w,np.dot(R_cov,w.T))) #计算最优投资组合的收益波动率
return np.array([Rp_opt,Vp_opt]) #以数组的格式输出结果def Vmin_f(w): #定义一个得到最小波动率的权重函数
return f(w)[1] #输出前面定义的函数f(w)结果的第二个元素cons_vmin=({
'type':'eq','fun':lambda x: np.sum(x)-1}) #仅设置权重和等于1的约束条件bnds=tuple((0,1) for x in range(len(R_mean))) #以元组格式输入权重的边界条件len(R_mean)*[1.0/len(R_mean),] #用于生成一个权重相等的数组[0.2, 0.2, 0.2, 0.2, 0.2]
result_vmin=sco.minimize(Vmin_f,len(R_mean)*[1.0/len(R_mean),] ,method='SLSQP',bounds=bnds,constraints=cons_vmin)
Rp_vmin=np.sum(R_mean*result_vmin['x'])
Vp_vmin=result_vmin['fun']
print('波动率在可行集是全局最小值时的投资组合预期收益率',round(Rp_vmin,4))
print('在可行集是全局最小的波动率',round(Vp_vmin,4))波动率在可行集是全局最小值时的投资组合预期收益率 -0.0236
在可行集是全局最小的波动率 0.2574
Rp_target=np.linspace(Rp_vmin,0.25,100) #生成投资组合的目标收益率数组
Vp_target=[]
for r in Rp_target:
cons_new=({
'type':'eq','fun':lambda x: np.sum(x)-1},{
'type':'eq','fun':lambda x: f(x)[0]-r}) #以字典格式输入预期收益率等于目标收益率的约束条件和权重的约束条件
result_new=sco.minimize(Vmin_f,len(R_mean)*[1.0/len(R_mean),],method='SLSQP',bounds=bnds,constraints=cons_new)
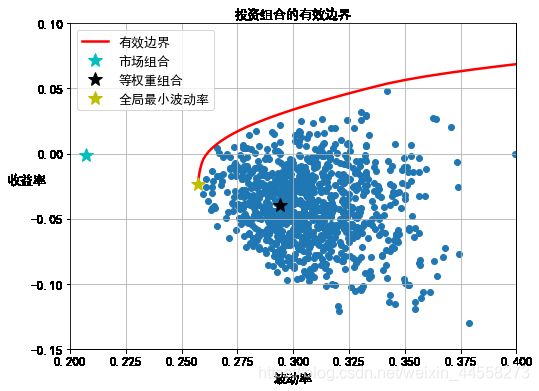
Vp_target.append(result_new['fun'])plt.figure(figsize=(8,6))
plt.scatter(Vp_list,Rp_list)
plt.plot(Vp_target,Rp_target,'r-',label=u'有效边界',lw=2.5)
plt.plot(Vm,Rm,'c*',label=u'市场组合',markersize=14)
plt.plot(vol_port,R_port,'k*',label=u'等权重组合',markersize=14)
plt.plot(Vp_vmin,Rp_vmin,'y*',label=u'全局最小波动率',markersize=14)
plt.xlabel(u'波动率',fontsize=13)
plt.ylabel(u'收益率',fontsize=13,rotation=0)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.xlim(0.2,0.40)
plt.ylim(-0.15,0.1)
plt.title(u'投资组合的有效边界',fontsize=13)
plt.legend(fontsize=13)
plt.grid('True')
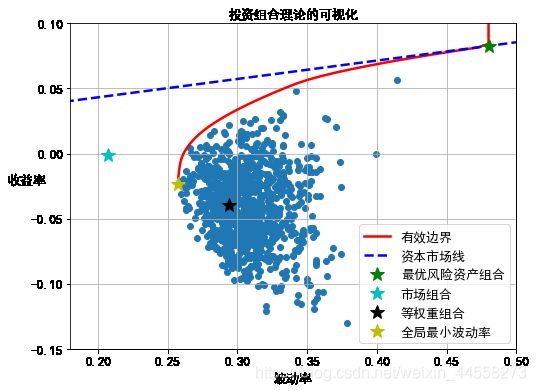
plt.show() 3、确定最优风险资产组合,并计算其夏普比率。
def F(w): #定义一个新的需要求解最优值的函数
Rf=0.015 #无风险利率为1.5%
w=np.array(w) #设置投资组合中每只股票的权重
Rp_opt=np.sum(w*R_mean) #计算最优组合的预期收益率
Vp_opt=np.sqrt(np.dot(w,np.dot(R_cov,w.T))) #计算最优投资组合收益波动率
SR=(Rp_opt-Rf)/Vp_opt #定义投资组合的夏普比率
return np.array([Rp_opt,Vp_opt,SR]) #以数组的格式输出结果def SRmin_F(w): #定义一个使负的夏普比率最小化的函数,即夏普比率最大
return -F(w)[2]cons_SR=({
'type':'eq','fun':lambda x: np.sum(x)-1})
result_SR=sco.minimize(SRmin_F,len(R_mean)*[1.0/len(R_mean),],method='SLSQP',bounds=bnds,constraints=cons_SR)Rf=0.015
slope=-result_SR['fun']
R_best=np.sum(R_mean*result_SR['x'])
V_best=(R_best-Rf)/slope
print('最优风险资产组合的预期收益率',round(R_best,4))
print('最优风险资产组合的波动率',round(V_best,4))
print('最优风险资产组合的夏普比率',round(slope,4))最优风险资产组合的预期收益率 0.0826
最优风险资产组合的波动率 0.48
最优风险资产组合的夏普比率 0.1408
print('最优风险资产组合中上海三毛的权重:',result_SR['x'][0])
print('最优风险资产组合中海尔智家的权重:',result_SR['x'][1])
print('最优风险资产组合中亿帆医药的权重:',result_SR['x'][2])
print('最优风险资产组合中凤凰传媒的权重:',result_SR['x'][3])
print('最优风险资产组合中东方财富的权重:',result_SR['x'][4])最优风险资产组合中上海三毛的权重: 4.2751539116065404e-19
最优风险资产组合中海尔智家的权重: 1.3877787807814457e-16
最优风险资产组合中亿帆医药的权重: 0.0
最优风险资产组合中凤凰传媒的权重: 6.692886964350196e-17
最优风险资产组合中东方财富的权重: 1.0
Rp_cml=np.linspace(0.015,0.3)
Vp_cml=(Rp_cml-Rf)/slopeplt.figure(figsize=(8,6))
plt.scatter(Vp_list,Rp_list)
plt.plot(Vp_target,Rp_target,'r-',label=u'有效边界',lw=2.5)
plt.plot(Vp_cml,Rp_cml,'b--',label=u'资本市场线',lw=2.5)
plt.plot(V_best,R_best,'g*',label=u'最优风险资产组合',markersize=14)
plt.plot(Vm,Rm,'c*',label=u'市场组合',markersize=14)
plt.plot(vol_port,R_port,'k*',label=u'等权重组合',markersize=14)
plt.plot(Vp_vmin,Rp_vmin,'y*',label=u'全局最小波动率',markersize=14)
plt.xlabel(u'波动率',fontsize=13)
plt.ylabel(u'收益率',fontsize=13,rotation=0)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.xlim(0.18,0.50)
plt.ylim(-0.15,0.1)
plt.title(u'投资组合理论的可视化',fontsize=13)
plt.legend(fontsize=13)
plt.grid('True')
plt.show() 4、比较市场组合、等权重组合以及最优风险资产组合的绩效。
夏普比率 SR = E ( R P ) − R f σ P \text {SR}=\frac{E\left(R_{P}\right)-R_{f}}{\sigma_{P}} SR=σPE(RP)−Rf
SR_market=(Rm-Rf)/Vm
SR_port=(R_port-Rf)/vol_port
SR_best=(R_best-Rf)/V_best
print('市场组合年平均夏普比率:',round(SR_market,4))
print('等权重组合年平均夏普比率:',round(SR_port,4))
print('最优风险资产组合年平均夏普比率:',round(SR_best,4))市场组合年平均夏普比率: 沪深300 -0.078
dtype: float64
等权重组合年平均夏普比率: -0.1849
最优风险资产组合年平均夏普比率: 0.1408
分析:由计算得出的夏普比率可以看出,最优风险资产组合的表现最好,夏普比率为正数,沪深300指数和等权重组合的夏普比率均为负数,等权重组合表现最差。
索提诺比率 SOR = E ( R P ) − R f σ L P \text {SOR}=\frac{E\left(R_{P}\right)-R_{f}}{\sigma_{LP}} SOR=σLPE(RP)−Rf
Data=pd.concat([SH['上海三毛'],HE['海尔智家'],YF['亿帆医药'],FH['凤凰传媒'],DF['东方财富'],HS['沪深300']],axis=1)r=np.log(Data/Data.shift(1))
r=r.dropna()
r_cov=r.cov()*252
print(r_cov) 上海三毛 海尔智家 亿帆医药 凤凰传媒 东方财富 沪深300
上海三毛 0.290920 0.041898 0.077502 0.057104 0.071736 0.035461
海尔智家 0.041898 0.120252 0.051979 0.027413 0.065728 0.050251
亿帆医药 0.077502 0.051979 0.195627 0.058504 0.095002 0.051618
凤凰传媒 0.057104 0.027413 0.058504 0.099974 0.066682 0.032778
东方财富 0.071736 0.065728 0.095002 0.066682 0.230380 0.067916
沪深300 0.035461 0.050251 0.051618 0.032778 0.067916 0.042970
r_port=0.2*(R['上海三毛']+R['海尔智家']+R['亿帆医药']+R['凤凰传媒']+R['东方财富'])def SOR(Rp,Rf,Vpl):
'''
计算索提诺比率(Sortino ratio)
Rp:表示投资组合的年化收益率;
Rf:表示年化无风险利率;
Vpl:表示投资组合收益率的年化下行标准差
'''
return (Rp-Rf)/Vpldef Vpl(R):
R_neg=R[R<0]
Vp_lower=np.sqrt(252)*np.sqrt(np.sum(R_neg**2)/len(R_neg))
return(Vp_lower)print('市场组合的索提诺比率:',round(SOR(Rm,Rf,Vpl(R_HS300)),4))
print('等权重组合的索提诺比率:',round(SOR(R_port,Rf,Vpl(r_port)),4))
print('最优风险资产组合的索提诺比率:',round(SOR(R_best,Rf,Vpl(r['东方财富'])),4))市场组合的索提诺比率: 沪深300 -0.111
dtype: float64
等权重组合的索提诺比率: -0.1788
最优风险资产组合的索提诺比率: 0.1389
分析:由计算得出的索提诺比率可以看出,最优风险资产组合的表现最好,索提诺比率为正数,沪深300指数和等权重组合的索提诺比率均为负数,等权重组合表现最差。
特雷诺比率 TR = E ( R P ) − R f β P \text {TR}=\frac{E\left(R_{P}\right)-R_{f}}{\beta_{P}} TR=βPE(RP)−Rf
import statsmodels.api as smdef TR(Rp,Rf,beta):
'''
计算特雷诺比率(Treynor ratio)
Rp:表示投资组合的年化收益率;
Rf:表示年化无风险利率;
beta:表示投资组合的贝塔值
'''
return (Rp-Rf)/betabeta_market=1
print('市场组合的特雷诺比率:',TR(Rm,Rf,beta_market))市场组合的特雷诺比率: 沪深300 -0.016163
dtype: float64
beta=[]
beta.append(0.035461/(Vm*Vm))
beta.append(0.050251/(Vm*Vm))
beta.append(0.051618/(Vm*Vm))
beta.append(0.032778/(Vm*Vm))
beta.append(0.067916/(Vm*Vm))beta_market=1
beta_port=0.2*(sum(beta))
beta_best=beta[4]print('市场组合的特雷诺比率:',round(TR(Rm,Rf,beta_market),4))
print('等权重组合的特雷诺比率:',round(TR(R_port,Rf,beta_port),4))
print('最优风险资产组合的特雷诺比率:',round(TR(R_best,Rf,beta_best),4))市场组合的特雷诺比率: 沪深300 -0.0162
dtype: float64
等权重组合的特雷诺比率: 沪深300 -0.0491
dtype: float64
最优风险资产组合的特雷诺比率: 沪深300 0.0428
dtype: float64
分析:由计算得出的特雷诺比率可以看出,最优风险资产组合的表现最好,特雷诺比率为正数,沪深300指数和等权重组合的特雷诺比率均为负数,等权重组合表现最差。
信息比率 TR = TD TE = E ( R P ) − E ( R B ) T E \text {TR}=\frac{\text{TD}}{\text{TE}}=\frac{E\left(R_{P}\right)-E\left(R_{B}\right)}{TE} TR=TETD=TEE(RP)−E(RB)
def IR(Rp,Rb,TD):
'''
计算信息比率(Information ratio)
Rp:表示投资组合的年化收益率;
Rb:表示基准组合的年化收益率;
TD:表示跟踪误差
'''
return (Rp-Rb)/TDTD_port=np.array(r_port)-np.array(r['沪深300'])
TE_port=TD_port.std()*np.sqrt(252)
TD_best=np.array(r['东方财富'])-np.array(r['沪深300'])
TE_best=TD_best.std()*np.sqrt(252)R_mean_HS300=R_HS300.mean()*252 #计算沪深30指数的年化收益率
R_mean_HS300=np.array(R_mean_HS300) #将沪深300指数年化收益率变成数组
IR_port=IR(R_port,R_mean_HS300,TE_port)
IR_best=IR(R_best,R_mean_HS300,TE_best)
print('等权重组合的信息比率:',round(IR_port[0],4))
print('最优风险资产组合的信息比率:',round(IR_best[0],4))等权重组合的信息比率: -0.2066
最优风险资产组合的信息比率: 0.2261
分析:以市场组合为基准,计算出等权重组合的信息比率为负值,表现比市场组合差,最优风险资产组合的信息比率为正值,表现比市场组合好
5、总结
为了实现投资组合理论,首先选出5只股票,根据日收盘价算出投资组合理论的主要变量,进而画出可行集、有效边界、资本市场线等,同时在图中标注出最优风险资产组合,市场组合,等权重组合以及最小方差组合。五只股票的投资组合方式优劣由图形可以直接看出:最优风险资产组合收益率>市场组合收益率>最小方差组合收益率>等权重组合收益率。计算四种比率:夏普比率,索提诺比率,特雷诺比率,信息比率也可以验证这一事实。由于所选择的五只股票相关系数较大,故未能很好地起到分散风险的效果,导致本次实验中等权重组合业绩表现最差。