NLP基础--文本特征提取&&中文分词&&word2vec原理

1. 文本特征提取

1.1 词集模型

例如One-Hot 编码，只要单个文本中单词出现在字典中，就将其置为1，不管出现多少次

首先，统计出语料中的所有词汇，然后对每个词汇编号，针对每个词建立V维的向量，向量的每个维度表示一个词，所以，对应编号位置上的维度数值为1，其他维度全为0。

优点是简单快捷，缺点是数据稀疏、耗时耗空间、不能很好地展示词与词之间的相似关系，且还未考虑到词出现的频率，因而无法区别词的重要性

1.2 BOW（Bag of Words）词袋模型

计算机只能读懂数字，怎么读懂句子呢？

Bag-of Words（BOW）定义：把文档看作一个袋子，并把文档中的语言打散为单词，不按顺序排列，抓取语言中的主要内容，忽视语言的格式和形式。文档中每个单词的出现都是独立的，不依赖于其它单词是否出现。也就是说，文档中任意一个位置出现的任何单词，都不受该文档语意影响而独立选择的。

例子：
维基百科上给出了如下例子:

John likes to watch movies. Mary likes too.
John also likes to watch football games.

根据上述两句话中出现的单词, 我们能构建出一个字典 (dictionary):

{“John”: 1, “likes”: 2, “to”: 3, “watch”: 4, “movies”: 5, “also”: 6, “football”: 7, “games”: 8, “Mary”: 9, “too”: 10}

该字典中包含10个单词, 每个单词有唯一索引, 注意它们的顺序和出现在句子中的顺序没有关联. 根据这个字典, 我们能将上述两句话重新表达为下述两个向量:

[1, 2, 1, 1, 1, 0, 0, 0, 1, 1]
[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]

这两个向量共包含10个元素, 其中第i个元素表示字典中第i个单词在句子中出现的次数. 如下面的表格所示。

在文本检索和处理应用中, 可以通过该模型很方便的计算词频.

适用场景：
现在想象在一个巨大的文档集合D，里面一共有M个文档，而文档里面的所有单词提取出来后，一起构成一个包含N个单词的词典，利用Bag-of-words模型，每个文档都可以被表示成为一个N维向量。

变为N维向量之后，很多问题就变得非常好解了，计算机非常擅长于处理数值向量，我们可以通过余弦来求两个文档之间的相似度，也可以将这个向量作为特征向量送入分类器进行主题分类等一系列功能中去。

总之通过有效的办法转换为向量之后，后面的一切都变得明朗起来了，因为至少得想办法让计算机理解吧！

代码：

# -*- coding: utf-8 -*-
# -*- coding: utf-8 -*-
from sklearn.feature_extraction.text import CountVectorizer

texts = ['John likes to watch movies, Mary likes too', 'John also likes to watch football games']
cv = CountVectorizer(analyzer='word', max_features=4000)
cv_fit = cv.fit_transform(texts)

print cv.get_feature_names()  # 获得上面稀疏矩阵的列索引，即特征的名字（就是特征词）
print '------------------------------------------------------------'
print cv_fit.toarray()  # 得到分词的系数矩阵-稠密向量矩阵表示
print '------------------------------------------------------------'
print cv_fit.toarray().sum(axis=0)  # 每个词在所有文档中的词频
print '------------------------------------------------------------'
print cv.vocabulary_  # 词汇表-也就是 字典顺序
print '------------------------------------------------------------'
print cv_fit  # 第一行结果分析： 第0个句子中，**词典中索引为8的元素**， 词频为1

输出结果：

我们直接用scikit-learn的CountVectorizer类来完成词袋模型的实现，这个类可以帮我们完成文本的词频统计与向量化。CountVectorize函数比较重要的几个参数为：

• decode_error，处理解码失败的方式，分为‘strict’、‘ignore’、‘replace’三种方式。
• strip_accents，在预处理步骤中移除重音的方式。默认为None，可设为ascii或unicode，将使用ascii或unicode编码在预处理步骤去除raw document中的重音符号。
• max_features，词袋特征个数的最大值。
• stop_words，设置停用词，设为english将使用内置的英语停用词，设为一个list可自定义停用词，设为None不使用停用词，设为None且max_df∈[0.7, 1.0)将自动根据当前的语料库建立停用词表。
• max_df，可以设置为范围在[0.0 1.0]的float，也可以设置为没有范围限制的int，默认为1.0。这个参数的作用是作为一个阈值，当构造语料库的关键词集的时候，如果某个词的document frequence大于max_df，这个词不会被当作关键词。如果这个参数是float，则表示词出现的次数与语料库文档数的百分比，如果是int，则表示词出现的次数。如果参数中已经给定了vocabulary，则这个参数无效。
• min_df，类似于max_df，参数min_df=n表示词必须要在至少n个文档中出现过，否则就不考虑。
• binary，默认为False，当与TF-IDF结合使用时需要设置为True。

CountVectorizer是通过fit_transform()函数将文本中的词语转换为词频矩阵，矩阵元素a[i][j] 表示j词在第i个文本下的词频。即各个词语出现的次数，通过get_feature_names()可看到所有文本的关键字，通过toarray()可看到词频矩阵的结果。

还可以使用现有的词袋模型，对其他文本进行特征提取。
代码：

vocabulary = cv.vocabulary_
j = ['John likes icecream and watch food movies']
new_cv = CountVectorizer(min_df=1, vocabulary=vocabulary)
X = new_cv.fit_transform(j)
print X.toarray()
print new_cv.get_feature_names()

结果：

缺点：
但是从上面我们也能够看出，在构造文档向量的过程中可以看到，我们并没有表达单词在原来句子中出现的次序，这也是词袋模型的缺点。因为它仅仅考虑了词频，没有考虑上下文的关系，因此会丢失一部分文本的语义。但是大多数时候，如果我们的目的是分类聚类，则词袋模型表现的很好。

1.3 TF-IDF

BOW模型有很多缺点，首先它没有考虑单词之间的顺序，其次它无法反应出一个句子的关键词，比如下面这个句子：

“John likes to play football, Mary likes too”

这个句子若用BOW模型，它的词表为：[‘football’, ‘john’, ‘likes’, ‘mary’, ‘play’, ‘to’, ‘too’]，则词向量表示为：[1 1 2 1 1 1 1]。若根据BOW模型提取这个句子的关键词，则为 “like”，但是显然这个句子的关键词应该为 “football”。

TF-IDF是一种统计方法，用以评估一个字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。

TF(Term frequency)即词频，其定义为某一个给定的词语在该文件中出现的频率。
$$tf(w)=\frac{单词w在文章中出现的次数}{该文章的总单词个数}$$
IDF（inverse document frequency，逆文本频率）IDF反应了一个词在所有文本中出现的频率，如果一个词在很多的文本中出现，那么它的IDF值应该低，比如“to”；反过来，如果一个词在比较少的文本中出现，那么它的IDF值应该高。比如一些专业的名词如“Machine Learning”。一个极端的情况，如果一个词在所有的文本中都出现，那么它的IDF值应该为0。其公式为：
$$idf(w)=log\frac{语料库中文档的总数}{包含词w的文档数+1}$$
那么tf-idf的整体计算公式为：
$$tf-idf(w)=tf(w)\ast idf(w)$$
TF-IDF值越大说明这个词越重要，也可以说这个词是关键词。

TF-IDF可以在用磁带模型向量化之后，再调用 TF-IDF进行特征处理，也可以直接使用TF-IDF完成向量化和预处理。

代码：

# -*- coding: utf-8 -*-
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer

corpus = ['John likes to watch movies, Mary likes too', 'John also likes to watch football games']

# 词袋化
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(corpus)
print vectorizer.get_feature_names()
print X.toarray()

# TF-IDF
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(X)
print tfidf.toarray()

from sklearn.feature_extraction.text import TfidfVectorizer

# 直接使用tf-idf
tfidf2 = TfidfVectorizer()
re = tfidf2.fit_transform(corpus)
print re.toarray()

运行结果：

缺点：
使用了IF-IDF并标准化以后，就可以使用各个文本的词特征向量作为文本的特征，进行分类或者聚类分析。
统计个数和计算频率两种方法虽然非常实用，但是也由其局限性导致词汇量可能变得非常大。词汇量过大又将导致需要非常大的矢量来编码文档，从而对内存产生很大的要求，同时拖慢算法的速度。此时可以使用哈希向量化。哈希向量化可以缓解TfidfVectorizer在处理高维文本时内存消耗过大的问题。

另外，按照传统TF-IDF的思想，往往一些生僻词的IDF(反文档频率)会比较高、因此这些生僻词常会被误认为是文档关键词。

2. 中文分词

中文分词和英文分词的典型区别：

• 分词方式不同，中文更难
  英文有天然的空格作为分隔符，但是中文没有。所以如何切分是一个难点，再加上中文里一词多意的情况非常多，导致很容易出现歧义。
• 英文单词有多种形态
  英文单词存在丰富的变形变换。为了应对这些复杂的变换，英文NLP相比中文存在一些独特的处理步骤，我们称为词形还原（Lemmatization）和词干提取（Stemming）。中文则不需要。
  词性还原：does，done，doing，did 需要通过词性还原恢复成 do。
  词干提取：cities，children，teeth 这些词，需要转换为 city，child，tooth”这些基本形态
• 中文分词需要考虑粒度问题
  例如「中国科学技术大学」就有很多种分法：
  中国科学技术大学
  中国 \ 科学技术 \ 大学
  中国 \ 科学 \ 技术 \ 大学
  粒度越大，表达的意思就越准确，但是也会导致召回比较少。所以中文需要不同的场景和要求选择不同的粒度。这个在英文中是没有的。

中文分词的难点：

• 没有统一的标准
  目前中文分词没有统一的标准，也没有公认的规范。不同的公司和组织各有各的方法和规则。
• 歧义词如何切分
  例如「兵乓球拍卖完了」就有2种分词方式表达了2种不同的含义：
  乒乓球 \ 拍卖 \ 完了
  乒乓 \ 球拍 \ 卖 \ 完了
• 新词的识别
  信息爆炸的时代，三天两头就会冒出来一堆新词，如何快速的识别出这些新词是一大难点。比如当年「蓝瘦香菇」大火，就需要快速识别。

下面开始介绍几种分词方法：

2.1 基于词典匹配的分词方法

该方法按照一定策略将待分析的汉字串与一个“充分大的”机器词典中的词条进行匹配，若在词典中找到某个字符串，则匹配成功。识别出一个词。根据扫描方向的不同分为正向匹配和逆向匹配。根据不同长度优先匹配的情况，分为最大（最长）匹配和最小（最短）匹配。根据与词性标注过程是否相结合，又可以分为单纯分词方法和分词与标注相结合的一体化方法。

常用方法有：正向最大匹配、逆向最大匹配、双向匹配

2.1.1 正向最大匹配（MM， MaximumMatching ）

对于输入的一段文本从左至右、以贪心的方式切分出当前位置上长度最大的词。正向最大匹配法是基于词表的分词方法 ，其分词原理是：单词的颗粒度越大，所能表示的含义越确切。

其算法描述如下：

step1: 从左向右取待切分汉语句的m个字符作为匹配字段，m为大机器词典中最长词条个数。
step2: 查找大机器词典并进行匹配。若匹配成功，则将这个匹配字段作为一个词切分出来。若匹配不成功，则将这个匹配字段的最后一个字去掉，剩下的字符串作为新的匹配字段，进行再次匹配，重复以上过程，直到切分出所有词为止。

2.1.2 逆向最大匹配（RMM，ReverseMaximum Matching）

在实际处理时，先将文档进行倒排处理，生成逆序文档。然后，根据逆序词典，对逆序文档用正向最大匹配法处理即可。

由于汉语中偏正结构较多，若从后向前匹配，可以适当提高精确度。所以，逆向最大匹配法比正向最大匹配法的误差要小。统计结果表明 ,单纯使用正向最大匹配的错误率为 1/16 9,单纯使用逆向最大匹配的错误率为 1/245。例如切分字段“硕士研究生产”，正向最大匹配法的结果会是“硕士研究生 / 产”，而逆向最大匹配法利用逆向扫描，可得到正确的分词结果“硕士 / 研究 / 生产”。

2.1.3 双向匹配

正向最大匹配法得到的分词结果和逆向最大匹配法的到的结果进行比较，从而决定正确的分词方法。
1.如果正反向分词结果词数不同，则取分词数量较少的那个。
2.如果分词结果词数相同 ：

• a.分词结果相同，就说明没有歧义，可返回任意一个。
• b.分词结果不同，返回其中单词较少的那个。

2.2 基于统计的分词方法

2.2.1 基于n-gram的分词方法

首先来简单了解一下n-gram是什么？

一个句子是否合理，就看看它的可能性大小如何”（引自数学之美）。由此，很容易理解语言模型的定义。什么是语言模型(Language Model)？假设 S 表示一个有意义的句子，由一连串特定顺序排列的词$w_1,w_2,...,w_n$组成，n为句子的长度。

则有:$p(s)=p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_1,w_2)\ast ...\ast p(w_n|w_1,w_2,...,w_{n-1})$，为了使序列 S 的概率最大化，我们也可以最小化 $L=\sum log(w|context(w))$，p(s) 和L都可以被称为语言模型。总而言之，语言模型就是建立了一个基于统计的模型去计算一个序列 S 的可能性。

N-gram就是语言模型。对于前面提到的语言模型从计算上来看，序列的前两个词的条件概率 $p(w_1),p(w_2|w_1)$不难计算，但是，越到后面的单词可能性越多，无法估算。因此，引入马尔可夫假设：任意一个词出现的概率只和它前面的n个词有关。

当 n=1, 一个一元模型（unigram model)即为 ：$p(w_1,w_2,...,w_n)={\prod }_{i=1}^{n}p(w_i)$

当 n=2, 一个二元模型（bigram model)即为 ：$p(w_1,w_2,...,w_n)={\prod }_{i=1}^{n}p(w_i|w_{i-1})$

当 n=3, 一个三元模型（trigram model)即为 ： $p(w_1,w_2,...,w_n)={\prod }_{i=1}^{n}p(w_i|w_{i-2},w_{i-1})$

假设n=2，于是 $p(s)=p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_2)\ast ...\ast p(w_n|w_{n-1})$，这就是N-gram模型中的二元模型(bigram)。

有了模型的定义，如何求解模型呢，即该如何计算条件概率呢？

根据定义：$p(w_i|w_{i-1})=\frac{p(w_{i-1},w_i)}{p(w_{i-1})}$，通过统计语料库(corpus)中的相应词和词对的频数，根据大数定理，只要统计量足够，相对频度就等于概率，即可得到$p(w_{i-1},w_i),p(w_{i-1})$。这其实就是模型根据训练数据集学习的过程。

由以上介绍的N-gram内容，我们能容易的理解N-gram的一个应用就是评估一个句子是否合理。我这里主要关注N-gram在分词上的应用。思路很简单，既然给定一个句子，N-gram可以计算出一个概率值，那只要列举出所有可能的分词方式，再根据所有可能的分词方式分别计算该句子的概率，选择使句子概率最大的分词方式作为最终分词结果就好了。

例子： 二元语言模型判断句子是否合理

假设现在有一个语料库，我们统计了下面的一些词出现的数量

下面的这些概率值作为已知条件：

p(i|)=0.25, p(english|food)=0.0011, p(food|english)=0.5,p(|food)=0.68,p(want|)=0.25

下面这个表给出的是基于Bigram模型进行计数之结果:

例如，其中第一行，第二列 表示给定前一个词是 “i” 时，当前词为“want”的情况一共出现了827次。据此，我们便可以算得相应的频率分布表如下:

比如说，我们就以表中的p(eat|i)=0.0036这个概率值讲解，从表一得出“i”一共出现了2533次，而其后出现eat的次数一共有9次，p(eat|i)=p(eat,i)/p(i)=count(i,eat)/count(i)=9/2533 = 0.0036。

下面我们通过基于这个语料库来判断s1=“ i want english food” 与s2 = " want i english food"哪个句子更合理：

首先来判断p(s1)
$P(s_1)=P(i|<s>)P(want|i)P(english|want)P(food|english)P(</s>|food)=0.25\times 0.33\times 0.0011\times 0.5\times 0.68=0.000031$

再来求p(s2)？

$P(s2)=P(want|<s>)P(i|want)P(english|want)P(food|english)P(</s>|food)=0.25\ast 0.0022\ast 0.0011\ast 0.5\ast 0.68=0.00000002057$

通过比较我们可以明显发现0.00000002057<0.000031,也就是说s1= "i want english food"更像人话。

N-gram的一个常见应用
搜索引擎（Google或者Baidu）、或者输入法的猜想\提示。你在用谷歌时，输入一个或几个词，搜索框通常会以下拉菜单的形式给出几个像下图一样的备选，这些备选其实是在猜想你想要搜索的那个词串。

再者，当你用输入法输入一个汉字的时候，输入法通常可以联系出一个完整的词，例如我输入一个“刘”字，通常输入法会提示我是否要输入的是“刘备”。通过上面的介绍，你应该能够很敏锐的发觉，这其实是以N-Gram模型为基础来实现的。比如下图：

那么原理是什么呢？也就是我打入“我们”的时候，后面的“不一样”，”的爱“这些是怎么出来的，怎么排序的？

实际上是根据语言模型得出。假如使用的是二元语言模型预测下一个单词：

排序的过程就是：

p(”不一样“|“我们”)>p(”的爱“|“我们”)>p(”相爱吧“|“我们”)>…>p(“这一家”|”我们“)，这些概率值的求法和上面提到的完全一样，数据的来源可以是用户搜索的log。

n-gram的n大小对性能的影响

• n更大的时候
  n 对下一个词出现的约束性信息更多，更大的辨别力，但是更稀疏，并且n-gram的总数也更多
• n更小的时候
  在训练语料库中出现的次数更多，更可靠的统计结果，更高的可靠性 ，但是约束信息更少

其中当N为特定值的时候，我们来看一下n-gram可能的总数，如下表

对于上图，我用一个例子来进行解释，加入目前词汇表中就只有三个单词，”我爱你“，那么bigram的总数是$3^2=9$个，有”我我“，我爱，我你，爱爱，爱你，爱我，你你，你我，你爱这9个,所以对应上面的表示是bigrams是$20000^2=400000000$,trigrams=$20000^3=8\ast 10e12$。

2.2.2 基于隐马尔科夫模型HMM的分词方法

首先用一个简单的例子来了解隐马尔科夫模型HMM：

（1）小明所在城市的天气有{晴天，阴天，雨天}三种情况，小明每天的活动有{宅，打球}两种选项。
（2）作为小明的朋友，我们只知道他每天参与了什么活动，而不知道他所在城市的天气是什么样的。
（3）这个城市每天的天气情况，会和前一天的天气情况有点关系。譬如说，如果前一天是晴天，那么后一天是晴天的概率，就大于后一天是雨天的概率。
（4）小明所在的城市，一年四季的天气情况都差不多。
（5）小明每天会根据当天的天气情况，决定今天进行什么样的活动。
（6）我们想通过小明的活动，猜测他所在城市的天气情况。

那么，城市天气情况和小明的活动选择，就构成了一个隐马尔科夫模型HMM，我们下面用学术语言描述下：

（1）HMM的基本定义： HMM是用于描述由隐藏的状态序列和显性的观测序列组合而成的双重随机过程。在前面的例子中，城市天气就是隐藏的状态序列，这个序列是我们观测不到的。小明的活动就是观测序列，这个序列是我们能够观测到的。这两个序列都是随机序列。
（2）HMM的假设一：马尔科夫性假设。当前时刻的状态值，仅依赖于前一时刻的状态值，而不依赖于更早时刻的状态值。每天的天气情况，会和前一天的天气情况有点关系。
（3）HMM的假设二：齐次性假设。状态转移概率矩阵与时间无关。即所有时刻共享同一个状态转移矩阵。小明所在的城市，一年四季的天气情况都差不多。
（4）HMM的假设三：观测独立性假设。当前时刻的观察值，仅依赖于当前时刻的状态值。小明每天会根据当天的天气情况，决定今天进行什么样的活动。
（5）HMM的应用目的：通过可观测到的数据，预测不可观测到的数据。我们想通过小明的活动，猜测他所在城市的天气情况。
注一：马尔科夫性：随机过程中某事件的发生只取决于它的上一事件，是“无记忆”过程。
注二：HMM被广泛应用于标注任务。在标注任务中，状态值对应着标记，任务会给定观测序列，以预测其对应的标记序列。
注三：HMM属于生成模型，是有向图。

HMM模型一共有三个经典的问题需要解决：
1） 评估观察序列概率。即给定模型=(,,Π)和观测序列={1,2,…}，计算在模型下观测序列出现的概率(|)。这个问题的求解需要用到前向后向算法，这个问题是HMM模型三个问题中最简单的。
2）模型参数学习问题。即给定观测序列={1,2,…}，估计模型=(,,Π)的参数，使该模型下观测序列的条件概率(|)最大。这个问题的求解需要用到基于EM算法的鲍姆-韦尔奇算法，这个问题是HMM模型三个问题中最复杂的。
3）预测问题，也称为解码问题。即给定模型=(,,Π)和观测序列={1,2,…}，求给定观测序列条件下，最可能出现的对应的状态序列，这个问题的求解需要用到基于动态规划的维特比算法，这个问题是HMM模型三个问题中复杂度居中的算法。

分词任务描述

原句： 我喜欢机器学习。
分词后： 我\喜欢\机器学习。

我们可以对每个字赋予一个标签，‘B’代表非词尾，‘E’表示词尾。则上述例子应该被标记为：

标记后： 我E喜B欢E机B器B学B习E。

假设观测序列为$O=\{O_1,O_2,...,O_N\}$，待预测的标签序列为$C=\{C_1,...,C_N\}$，其中$C_i\in \{B,E\}$。那么我们的目标是$C=argma{x}_{C}P(C\mid O)$。

由贝叶斯公式$P(C\mid O)=\frac{P(O\mid C)P(C)}{P(O)}$ 。因为观测序列不变则省略分母$P(O)$。

由马尔科夫假设知，当前状态只与前一时刻状态有关，则$P(C)=P(C_1,C_2,...,C_N)=P(C_1)\ast P(C_2\mid C_1)\ast P(C_3\mid C_2)\ast ...\ast P(C_N\mid C_{N-1})$，
其中$P(C_i\mid C{i}_1)$为状态转移概率。由观测独立假设知，当前的观测输出只与当前状态有关，则$P(O\mid C)=P(O_1,...,O_N\mid C_1,...,C_N)=P(O_1\mid C_1)\ast P(O_2\mid C_2)\ast ...\ast P(O_N\mid C_N)$，其中$P(O_i\mid C_i)$为观测概率。

至此，分词问题可以归结于标注问题，是HMM的解码问题，使用到了维特比（Viterbi）算法。其中初始状态概率${\pi }_i$， 状态转移概率$P(C_i|C_{i-1})$和观测概率$P(O_i|C_i)$是HMM模型的参数，可以由极大似然估计的统计方法（监督学习，训练集包含观测序列和对应的标签序列），或者EM/Baum-Welch/前向后向算法（非监督学习，数据集只有观测序列）求得。

实际问题中，我们使用4种标签 {B,E,M,S}，分别表示：

B：词语的开始
E：词语的结束
M：词语的中间部分
S：单个字组成的单词

举例：我S喜B欢E机B器M学M习E

实际任务中，状态转移矩阵和观测矩阵可以由监督学习得来。这里我们可以用bi-gram模型：$P(C_i|C_{i-1})=\frac{Count(C_{i-1},C_i)}{Count(C_{i-1})}$，$P(O_i|C_i)=\frac{C_i,O_i}{C_i}$ , 其中考虑到未出现的bigram对，这里可以使用不同的smooting技术（add-1， back-off…）。

接着，得到HMM模型参数后，就可以通过Viterbi算法来找到最佳的标签序列了，继而完成对句子的分词。

3. word2vec原理

在自然语言处理任务中，文本向量化往往是任务中必不可少的基础工作，因此如何更好地将文本向量化就显得尤为重要。词是自然语言文本中最小的语义单元，自然语言文本是由词序列构成的，因此如果能够完成对词的向量化，那么文本向量化的任务也就迎刃而解了。

word2vectory属于是文本向量化的内容，但是之所以单独放在一章的原因是：在第一部分文本特征化中，我们介绍了词袋模型和TF-IDF，使用较多的也是TF-IDF表示的词向量，但是TF-IDF只给出了某个词的重要性程度，并没有表示出词语的语义信息。Word2Vec方法是一类神经网络模型的名称，它给定一个未标记的训练语料库，为语料库中的每个单词生成一个向量，对其语义信息进行编码。

编码后的词向量可以：

1. 通过计算两个词对应的词向量之间的相似性，可以衡量两个词之间的语义相似度
2. 我们可以使用这些词向量作为各种有监督的NLP任务的特征，例如文档分类、命名实体识别和情感分析。

词袋模型（bag of words）是最早的以词为基本处理单元的文本向量化方法，词袋模型通过先构建一个包含语料库中所有词的词典，然后根据词典完成对每个词的向量化，进而完成文本向量化。具体的过程和代码已经在第一部分中介绍过了，这里不再赘述。

词袋模型的几个问题：

• 维度灾难：如果词典中有很多个词，那么每个词都是一个维度很高的向量
• 未保留词序：只将文本看成是一袋子词
• 语义鸿沟：通过向量表示无法体现两个词是否为同义词

为了解决词袋模型的问题，通过语言模型构建词向量的方式出现了。

假设 S 表示一个有意义的句子，由一连串特定顺序排列的词$w_1,w_2,...,w_n$组成，n为句子的长度。
则有:$p(s)=p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_1,w_2)\ast ...\ast p(w_n|w_1,w_2,...,w_{n-1})=p(w_1)\ast p(w_2|w_1)\ast p(w_3|w_1^2)\ast ...\ast p(w_n|w_1^{n-1})$

其中$w_m^n$表示从$w_m$到$w_n$的序列。

那么计算$p(s)$的概率就转变为计算$p(w_1)$和$p(w_i|w_1^{i-1}),i\in \{2,3,...,n\}$。计算$p(w_i|w_1^{i-1})$本文介绍n-gram模型和神经网络模型两种方式。

3.1 统计语言模型之n-gram语言模型

在第二章中，本文介绍了关于n-gram如何进行分词，了解了n-gram的原理。这里就简单复述一下。

利用贝叶斯公式，有$p(w_i|w_1^{i-1})=\frac{p(w_i,w_{i-1},...,w_1)}{p(w_1^{i-1})}$
再根据大数定律，用频数代替频率，有$p(w_i|w_1^{i-1})=\frac{count(w_i,w_{i-1},...,w_1)}{count(w_1^{i-1})}$

公式$p(w_i|w_1^{i-1})$表示词$w_i$出现的概率和它前面所有的词$w_1^{i-1}$有关。 表示$w_1^i$在语料库中出现的次数，当i很大时，计算$count(w_1^i)$是非常耗时间的。

而n-gram模型假设一个词的出现只与它前面的固定数目的词有关系，相当于做了一个n-1阶的马尔科夫的假设，认为一个词的出现只与它前面n-1个词相关。通过n-gram模型的简化之后，计算$p(w_i|w_1^{i-1})$的复杂度大大减小了。

3.2 神经网络语言模型NNLM

NNLM通过分布式表示（distributed representations）（分布式表示大概就是说单独看其中一维的话没什么含义，但是组合到一起的vector就表达了这个词的语义信息）解决了维度灾难（curse of dimensionality）的问题。通过词向量矩阵C，将词汇表中的V个单词映射为V个m维的词向量（feature vector）。

同样使用n-gram表示，但是NNLM却是共享参数矩阵C。相反，统计语言模型却需要用词矩阵表示每一个句子，空间代价太大。

为了说明，下面定义符号：
训练集是许多由词$w_1\dots w_T$构成的句子，其中$w_t\in V$，词汇表V是有限个不重复词组成的集合。

训练目标是学到一个很好的模型:$f(w_t,\dots ,w_t-n+1)=\hat{p}(w_t|w_{t-n+1}^{t-1})$

取 $\hat{p}(w_t|w_{t-n+1}^{t-1})$的几何平均值作为困惑度（perplexity）,即log似然的几何平均的指数。

模型中的唯一常数是对于任意的组合$w_1^{t-1}$,保证${\sum }_{t=1}^{|V|}f(t,w_{t-1},\dots ,w_{t-n+1})=1,f>0$

通过条件概率的乘积，我们能够得到许多词组合成句子的联合概率。
将$f(w_t,\dots ,w_{t-n+1})=\hat{p}(w_t|w_{t-n+1}^{t-1})$分解成两部分：

• 词汇表V中的第i个单词->词向量$C(i)\in R^m$。 C(i)表示每个词i的分布式词向量(distributed feature vector),C是一个拥有|V|×m参数的词向量矩阵。
• 第i个词的上文的向量形式为：$(C(w_{i-n+1}),\dots ,C(w_{i-1}))$，已知词汇表V中第i个词在已知前n-1个词时的条件概率是$p(w_i|w_{i-n+1}^{i-1})$，则定义函数$g(i,C(w_{i-n+1}),\dots ,C(w_{i-1}))$为此时第i个词的词向量，即：$f(w_i,w_{i-1},\dots ,w_{i-n+1})=g(i,C(w_{t-n+1}),\dots ,C(w_{t-1}))$

因此，函数f是C和g的复合函数，并且C是所有词共享的一个参数矩阵。函数g可以用一个前馈网络(FNN)或循环神经网络(RNN)来实现。
设网络中所有参数为$\omega$，则整个NNLM的参数$\theta =(C,\omega )$。

模型的训练目标：$$argma{x}_{\theta }L=\frac{1}{T}\sum _t^{|V|}logf(w_t,\dots ,w_{t-n+1};\theta )+R(\theta )$$
其中R(θ)为正则化惩罚项。

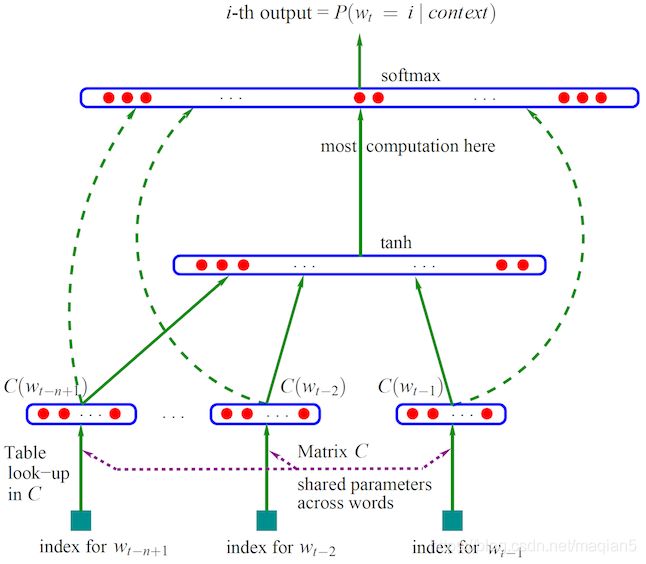
接下来来解释NNLM的模型示意图：

• 输入层：将$C(w_{t-n+1}),\dots ,C(w_{t-1})$这n-1个词向量首尾相接拼起来形成一个$(n-1)m$的一维？向量x。
• 隐藏层：输入$o=d+H\ast x$，d为h维的隐层偏置项，H为$h\ast (n-1)m$维的隐层参数；输出$a=tanh(o)$
• 输出层：用Softmax做V分类，模型大部分计算都在这一层；$y_i$表示下一个词为i的未归一化log概率：$y=b+W\ast x+U\ast tanh(d+H\ast x)$。其中，U为$|V|\times h$维的输出层参数矩阵，b为|V|维的输出层偏置项。模型考虑了从输入层直接到输出层的概率，W即为输入层直连输出层的$|V|\times (n-1）m$维参数矩阵。

综上：$\theta =(b,d,W,U,H,C)$，总参数个数为:$|V|(1+mn+h)+h(1+(n-1)m)$。

用随机梯度上升求解：$\theta \leftarrow \theta +ϵ\frac{\partial log\hat{P}(w_t|w_{t-n+1}^{t-1})}{\partial \theta }$

收敛后得到了词向量矩阵C即为我们NNLM中最重要的参数，通过矩阵C可以完成词（Word）到向量（Vector）的转换。

3.3 word2vecmoxing之CBOW与Skip-Gram

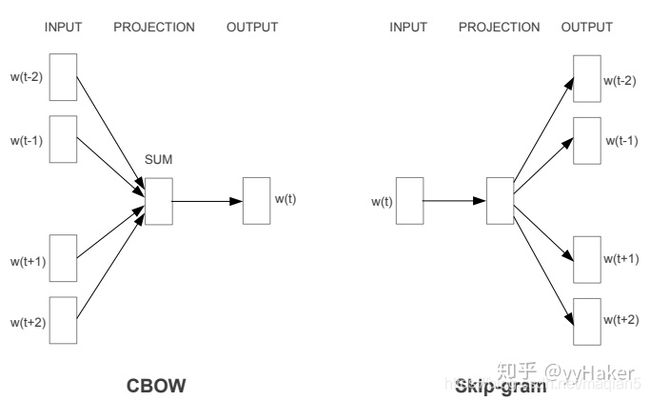
word2vectory的网络结构其实和神经网络语言模型（NNLM）是基本类似的。不过这里需要指出：尽管网络结构接近，而且也是做语言模型任务，但是其训练方法不太一样。

word2vectory有两种训练方法，一种叫CBOW，核心思想是把一个句子里面的词扣掉，然后用这个词的上文和下文去预测这个被抠掉的这个词；第二种叫做Skip-gram，和CBOW正好反过来，输入某个单词，要求网络预测它的上下文单词。而NNLM是怎么干的？是输入一个单词的上文，去预测这个词。这是有显著差异的！

为什么word2vectory这么处理？原因很简单，因为word2vectory和NNLM不一样，NNLM的主要任务是学习一个解决语言模型任务的网络结构，语言模型就是要看到上文预测下文，而词向量只是一个无心插柳的副产品，是个bonus。但是啊，word2vectory的目标不一样，说白了，它单纯就是要获得词向量的，这是主产品，所以它完全可以这么随性地去训练网络。 所以，word2vectory 本质上也是一个神经网络语言模型，但是它的目标并不是语言模型本身，而是词向量；因此，其所作的一系列优化，都是为了更快更好的得到词向量。

接下来，我们来具体看看，word2vec提供的两套模型：CBOW和Skip-Gram，其基本思想如下：

• CBOW在已知 $context(w)$的情况下，预测$w$
• Skip-Gram在已知$w$的情况下预测 $context(w)$

3.3.1 CBOW（Continuous Bag-of-Words）

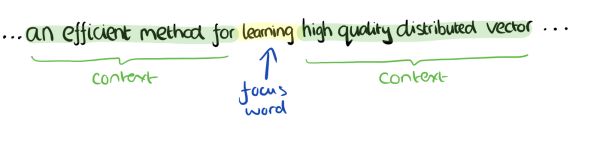
CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量，而输出就是这特定的一个词的词向量。比如下面这段话，我们的上下文大小取值为4，特定的这个词是"Learning"，也就是我们需要的输出词向量,上下文对应的词有8个，前后各4个，这8个词是我们模型的输入。由于CBOW使用的是词袋模型，因此这8个词都是平等的，也就是不考虑他们和我们关注的词之间的距离大小，只要在我们上下文之内即可。

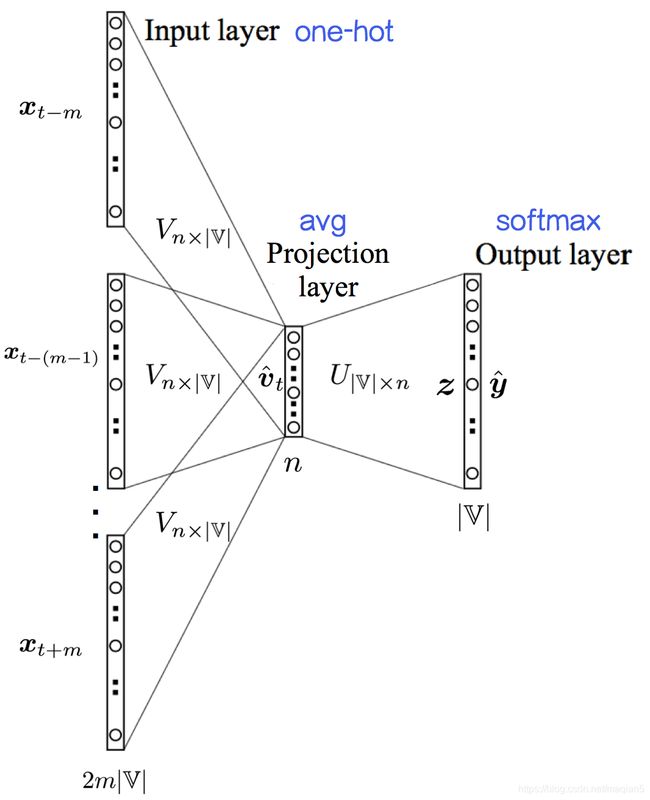
CBOW 与神经网络语言模型不同的是，CBOW去掉了最耗时的非线性隐藏层。

• 输入层：2m个节点(m为窗口大小)，每个词向量使用one-hot编码表示，一共有$2m|V|$个神经元结点
• 输入层到隐含层：NNLM模型的隐含层做了经典神经网络的乘加操作，并使用tanh进行激活。CBOW则是直接对2m个词向量做平均值处理。$V_{n\times |V|}$是输入层到隐含层的参数矩阵，隐含层的输出为$\hat{v}=\frac{1}{2m}\sum V\times x_{t+i}$，其中$i\in \{-m,-m+1,...,m-1,m\}\text{}\{0\}$。隐含层有n个神经元节点。
• 隐含层到输出层：输出层有$|V|$个神经元节点。最终结果 $\hat{y}=softmax(U\times \hat{v})$，其中$U$是一个$|V|\times n$维的矩阵。
  输出层的向量 $\hat{y}$ 与输入层的向量为 $x_{t+i}$虽然维度是一样的，但是$\hat{y}$ 并不是one-hot向量，并且向量$\hat{y}$ 中的每个元素都是有意义的，第i个位置上的数值表示中心词是词$w_i$的概率。

有了$\hat{y}$，我们就可以构建损失函数，然后再通过反向传播算法，就可以求出模型的参数$U$和$V$。这样当我们有新的需求，要求出某2m个词对应的最可能的输出中心词时，我们可以通过一次DNN前向传播算法并通过softmax激活函数找到概率最大的词对应的神经元即可。因为这种方法涉及到softmax层，softmax每次计算都要遍历整个词表，代价十分昂贵，所以实现的时候我们不用这种方法，而是后面要介绍到的层次softmax和负采样。

3.3.2 skip-gram

Skip-Gram模型和CBOW的思路是反着来的，即输入是特定的一个词的词向量，而输出是特定词对应的上下文词向量。还是上面的例子，我们的上下文大小取值为4， 特定的这个词"Learning"是我们的输入，而这8个上下文词是我们的输出。

从下图中可以看出，skip-gram与CBOW的模型正好是反过来的。假设取窗口m=2，那么skip-gram预测的就是$p(w_{t-2}|w_t),p(w_{t-1}|w_t),p(w_{t+1}|w_t),p(w_{t+2}|w_t)$。

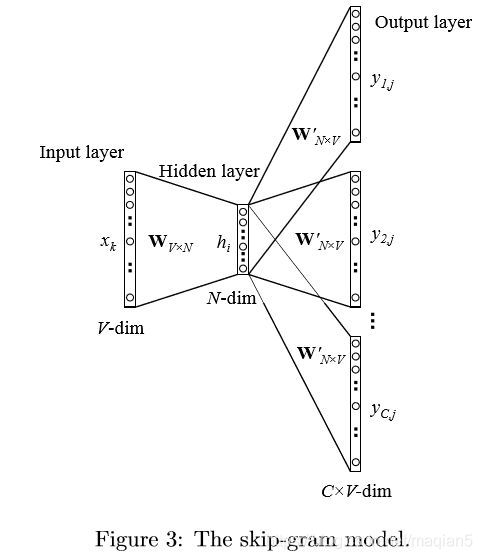
• 输入层：输入层为中心词的one-hot编码表示，维度为$1\times |V|$。V表示词汇表的大小。
• 输入层到隐含层：输入层到隐含层的操作是进行矩阵的乘积，$h=W^T\times x_k$，其中$W$是一个$V\times N$的二维参数矩阵，N为隐含层的神经元节点个数。
• 隐含层到输出层：最终结果 $y=softmax(W^{{}^{\prime }}\times h)$。其中$W^{{}^{\prime }}$是一个$N\times V$的参数矩阵。
  这个地方存疑：在刘建平的博客中写的是“输出层有词汇表大小个神经元”，即有V个，而在另一篇博客(本文参考的是这一篇)中，如上图所示，输出层的神经元数量是C×V个。
  同样的，输出层的向量 $y$与输入层的向量为 $x_k$ 虽然维度是一样的，但是 $y$ 并不是one-hot向量，并且向量 $y$ 中的每个元素都是有意义的。

3.4 word2vec之分层的softmax模型（Hierarchical Softmax）

3.4.1 分层softmax的CBOW模型

首先，层次softmax是一棵huffman树，树的叶子节点是训练文本中所有的词，非叶子节点都是一个逻辑回归二分类器，每个逻辑回归分类器的参数都不同，分别用${\theta }_{\ast }$ 表示。假定分类器的输入是向量 $h$，记逻辑回归分类器输出的结果为$\delta ({\theta }_{\ast }h)$ ，将向量 $h$传递给节点的左孩子的概率为$\delta ({\theta }_{\ast }h)$，否则传递给节点的右孩子的概率是 $1-\delta ({\theta }_{\ast }h)$。重复这个传递的流程直到叶子节点。

如下图所示，为采用分层softmax的CBOW模型。将隐藏层的向量 $h$ 直接传给了一个层次softmax，层次softmax的复杂度为 $O(log(V))$ 。

层次softmax采样到每个词的概率分别如下：

采样到 I 的概率 $p(I|context)=(1-\delta ({\theta }_{1}h))(1-\delta ({\theta }_{3}h))$

采样到 eat 的概率 $p(eat|context)=(1-\delta ({\theta }_{1}h))\delta ({\theta }_{3}h)$

采样到 to 的概率$p(to|context)=\delta ({\theta }_{1}h)(1-\delta ({\theta }_{2}h))$

采样到 like 的概率$p(like|context)=\delta ({\theta }_{1}h)\delta ({\theta }_{2}h)(1-\delta ({\theta }_{4}h))$

采样到 apple 的概率 $p(apple|context)=\delta ({\theta }_{1}h)\delta ({\theta }_{2}h)\delta ({\theta }_{4}h)$

如果我们要预测的词是 to ，那么我们就要让 $p(to|context)$ 尽量大一点，所以现在我们的任务转化为了训练$V-1$个逻辑回归分类器。

分层softmax的CBOW模型形式化的表示如下：

• 输入：基于CBOW的语料训练样本，词向量的维度大小，CBOW的上下文大小2,步长
• 输出：霍夫曼树的内部节点模型参数，所有的词向量

算法步骤：

1. 基于语料训练样本建立霍夫曼树。形成哈弗曼编码d
2. 随机初始化所有的模型参数，所有的词向量
3. 进行梯度上升迭代过程，对于训练集中的每一个样本((),)做如下处理：
       a) e=0， 计算$x_w=\frac{1}{2c}{\sum }_{i=1}^{2c}{x}_i$
       b) for j = 2 to $l_w$, 计算：$f=\delta (x_w^T{\theta }_{j-1}^w)$，
                                             $g=(1-d_j^w-f)\eta$，
                                             $e=e+g{\theta }_{j-1}^w$，
                                             ${\theta }_j^w={\theta }_{j-1}^w+g{x}_w$
       c) 对于()中的每一个词向量$x_i$(共2c个)进行更新：$x_i=x_i+e$
       d) 如果梯度收敛，则结束梯度迭代，否则回到步骤3继续迭代。

3.4.2 分层softmax的skip-gram模型

Skip-Gram模型和CBOW模型其实是反过来的。在做CBOW模型前，我们需要先将词汇表建立成一颗霍夫曼树。Skip-Gram模型也一样需要将词汇表建立成一颗霍夫曼树。

对于从输入层到隐藏层（投影层），这一步比CBOW简单，由于只有一个词，所以，即$x_w$就是词$w$对应的词向量。

第二步，通过梯度上升法来更新我们的${\theta }_{j-1}^w$和$x_w$，注意这里的$x_w$周围有2个词向量，此时如果我们期望$p(x_i|x_w),i=1,2,...,2c$最大。此时我们注意到由于上下文是相互的，在期望$p(x_i|x_w),i=1,2,...,2c$最大化的同时，反过来我们也期望$p(x_w|x_i),i=1,2,...,2c$最大。那么是使用$p(x_i|x_w)$好还是$p(x_w|x_i)$好呢，word2vec使用了后者，这样做的好处就是在一个迭代窗口内，我们不是只更新$x_w$一个词，而是$x_i,i=1,2,...2c$共2个词。这样整体的迭代会更加的均衡。因为这个原因，Skip-Gram模型并没有和CBOW模型一样对输入进行迭代更新，而是对2个输出进行迭代更新。

总结下基于Hierarchical Softmax的Skip-Gram模型算法流程，梯度迭代使用了随机梯度上升法：

• 输入：基于Skip-Gram的语料训练样本，词向量的维度大小，Skip-Gram的上下文大小2,步长
• 输出：霍夫曼树的内部节点模型参数，所有的词向量

算法步骤：

1. 基于语料训练样本建立霍夫曼树。
2. 随机初始化所有的模型参数，所有的词向量,
3. 进行梯度上升迭代过程，对于训练集中的每一个样本(,())做如下处理：
      a) for i =1 to 2c:
              i) e=0
              ii)for j = 2 to $l_w$, 计算：$f=\delta (x_w^T{\theta }_{j-1}^w)$，
                                                 $g=(1-d_j^w-f)\eta$，
                                                 $e=e+g{\theta }_{j-1}^w$，
                                                 ${\theta }_j^w={\theta }_{j-1}^w+g{x}_w$
              iii)          $x_i=x_i+e$
      b) 如果梯度收敛，则结束梯度迭代，否则回到步骤a)继续迭代。

3.5 word2vec之负采样（Negative Sampling）

分层Softmax的的缺点：使用霍夫曼树来代替传统的神经网络，可以提高模型训练的效率。但是如果我们的训练样本里的中心词是一个很生僻的词，那么就得在霍夫曼树中辛苦的向下走很久了。能不能不用搞这么复杂的一颗霍夫曼树，将模型变的更加简单呢？

负采样就是这么一种求解word2vec模型的方法，它摒弃了霍夫曼树，采用了Negative Sampling（负采样）的方法来求解。

假设我们有一个训练样本，中心词是$w$，它周围上下文共有2个词，记为$context(w)$。由于这个中心词$w$和$context(w)$相关存在，因此它是一个真实的正例。通过Negative Sampling采样，我们得到neg个和$w$不同的中心词$w_i,i=1,2,...,neg$，这样$context(w)$和$w_i$就组成了neg个并不真实存在的负例。利用这一个正例和neg个负例，我们进行二元逻辑回归，得到负采样对应每个词$w_i$对应的模型参数${\theta }_i$，和每个词的词向量。

从上面的描述可以看出，Negative Sampling由于没有采用霍夫曼树，每次只是通过采样neg个不同的中心词做负例，就可以训练模型，因此整个过程要比Hierarchical Softmax简单。

不过有两个问题还需要弄明白：1）如何通过一个正例和neg个负例进行二元逻辑回归呢？ 2） 如何进行负采样呢？

3.5.1 基于Negative Sampling的模型梯度计算

Negative Sampling也是采用了二元逻辑回归来求解模型参数，通过负采样，我们得到了neg个负例$(context(w),w_i),i=1,2,...,neg$。为了统一描述，我们将正例定义为$w_0$。

在逻辑回归中，我们的正例应该期望满足：$p(context(w_0),w_i)=\delta (x_{w_0}^T{\theta }^{w_i}),y_i=1,i=0$

我们的负例期望满足：$p(context(w_0),w_i)=1-\delta (x_{w_0}^T{\theta }^{w_i}),y_i=0,i=1,2,...,neg$

我们期望可以最大化下式：${\prod }_{i=0}^{neg}P(context(w_0),w_i)=\delta (x_{w_0}^T{\theta }^{w_0}){\prod }_{i=1}^{neg}(1-\delta (x_{w_0}^T{\theta }^{w_i}))$

利用逻辑回归和上一节的知识，我们容易写出此时模型的似然函数为：
${\prod }_{i=0}^{neg}\delta (x_{w0}^T{\theta }^{w_i}{)}^{y_i}(1-\delta (x_{w_0}^T{\theta }^{w_i}){)}^{1-y_i}$

此时对应的对数似然函数为：$L={\sum }_{i=0}^{neg}{y}_{i}log(\delta (x_{w_0}^T{\theta }^{w_i}))+(1-y_i)log(1-\delta (x_{w_0}^T{\theta }^{w_i}))$

和Hierarchical Softmax类似，我们采用随机梯度上升法，仅仅每次只用一个样本更新梯度，来进行迭代更新得到我们需要的$x_{w_i},{\theta }^{w_i},i=0,1,2,...,neg$, 这里我们需要求出$x_{w_0},{\theta }^{w_i},i=0,1,...,neg$的梯度。用梯度上升法进行迭代来一步步的求解。

3.5.2 Negative Sampling负采样方法

现在我们来看看如何进行负采样，得到neg个负例。word2vec采样的方法并不复杂，如果词汇表的大小为,那么我们就将一段长度为1的线段分成份，每份对应词汇表中的一个词。当然每个词对应的线段长度是不一样的，高频词对应的线段长，低频词对应的线段短。每个词的线段长度由下式决定：$len(w)=\frac{count(w)}{{\sum }_{u\in vovab}count(u)}$。

在word2vec中，分子和分母都取了3/4次幂如下：$len(w)=\frac{count(w{)}^{\frac{3}{4}}}{{\sum }_{u\in vovab}count(u{)}^{\frac{3}{4}}}$。在采样前，我们将这段长度为1的线段划分成等份，这里>>，这样可以保证每个词对应的线段都会划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。在采样的时候，我们只需要从个位置中采样出个位置就行，此时采样到的每一个位置对应到的线段所属的词就是我们的负例词。在word2vec中，取值默认为$10^8$。

3.5.3 基于Negative Sampling的CBOW模型

• 输入：基于CBOW的语料训练样本，词向量的维度大小$M_{count}$，CBOW的上下文大小2,步长, 负采样的个数neg
• 输出：词汇表每个词对应的模型参数，所有的词向量

算法步骤：

1. 随机初始化所有的模型参数$\theta$，所有的词向量$w$
2. 对于每个训练样本$(context(w_0),w_0)$，负采样出neg个负例中心词$w_i,i=1,2,...,neg$
3. 进行梯度上升迭代过程，对于训练集中的每一个样本$(context(w_0),w_0,w_1,...,w_{neg})$做如下处理：
       a)$e=0$，计算$x_{w_0}=\frac{1}{2c}{\sum }_{i=0}^{2c}{x}_i$
       b) for i=0 to neg，计算:$f=\delta (x_{w_0}^T{\theta }^{w_i})$
                                             $g=(y_i-f)\eta$
                                             $e=e+g{\theta }^{w_i}$
                                             ${\theta }^{w_i}={\theta }^{w_i}+g{x}_{w_0}$
      c) 对于$context(w)$中的每一个词向量$x_k$(共2c个)进行更新：$x_k=x_k+e$
      d) 如果梯度收敛，则结束梯度迭代，否则回到步骤3继续迭代。

3.5.4 基于Negative Sampling的skip-gram模型

• 输入：基于Skip-Gram的语料训练样本，词向量的维度大小$M_{count}$，Skip-Gram的上下文大小2,步长， , 负采样的个数neg。
• 输出：词汇表每个词对应的模型参数，所有的词向量

算法步骤：

1. 随机初始化所有的模型参数$\theta$，所有的词向量$w$
2. 对于每个训练样本$(context(w_0),w_0)$,负采样出neg个负例中心词$w_i,i=1,2,...,neg$
3. 进行梯度上升迭代过程，对于训练集中的每一个样本$(context(w_0),w_0,w_1,...,w_{neg})$做如下处理：
       a)for i = 1 to 2c
             i) $e=0$
             ii) for j=0 to neg， 计算：
                     $f=\delta (x_{w_{0i}}^T{\theta }^{w_j})$
                     $g=(y_j-f)\eta$
                     $e=e+g{\theta }^{w_j}$
                     ${\theta }^{w_j}={\theta }^{w_j}+g{x}_{w_{0i}}$
             iii) 词向量更新：$x_{w_{0i}}=x_{w_{0i}}+e$
       b)如果梯度收敛，则结束梯度迭代，算法结束，否则回到步骤a继续迭代。

参考

1. https://zhuanlan.zhihu.com/p/43675887
2. https://zhuanlan.zhihu.com/p/29933242
3. https://blog.csdn.net/shenfuli/article/details/96209532
4. https://blog.csdn.net/qq_27586341/article/details/90286751
5. https://blog.csdn.net/u012328159/article/details/84719494
6. https://www.jianshu.com/p/b2da4d94a122
7. https://easyai.tech/ai-definition/tokenization/#qubie
8. https://blog.csdn.net/DianaCody/article/details/40950169
9. https://zhuanlan.zhihu.com/p/57417045
10. https://zhuanlan.zhihu.com/p/32829048
11. https://zhuanlan.zhihu.com/p/57417045
12. https://zhuanlan.zhihu.com/p/87632700
13. https://blog.csdn.net/u013166817/article/details/85805513
14. https://www.cnblogs.com/pinard/p/6945257.html
15. https://zhuanlan.zhihu.com/p/44599645
16. https://www.cnblogs.com/pinard/p/7160330.html
17. http://www.pengjingtian.com/2016/09/17/nnlm/
18. https://zhuanlan.zhihu.com/p/59802406
19. https://www.cnblogs.com/Determined22/p/5804455.html
20. https://www.cnblogs.com/pinard/p/7243513.html
21. https://www.cnblogs.com/pinard/p/7249903.html