Fisher信息度量下的对抗攻击

该文是我投稿于人工智能前沿的一篇文章，如果大家有什么问题想要跟我讨论，可以留言跟我一起交流。

核心思想

   本论文从信息几何的角度为深度模型的脆弱性提出了一种合理的解释。通过将数据空间视为具有从神经网络诱导的Fisher信息度量的非线性空间，并提出另一种攻击算法单步谱攻击（OSSA），该方法由Fisher信息矩阵的约束二次型形式描述，其中最优的对抗扰动由第一特征向量给出，并且脆弱性由特征值反映。特征值越大，模型越容易被相应的特征向量攻击。
利用该属性，我们还提出了一种特征值作为特征的对抗性检测方法。

论文的贡献

在深度模型脆弱性的解释中，引入Fisher信息矩阵(FIM)具有3个重大意义:

• FIM是KL散度的Hssian矩阵，它是概率分布有意义的度量方式。

• FIM是对称且半正定的，使得对矩阵的优化更加简单有效。

• 只要输出的概率可能性没有变化，FIM对于重新参数化也是不变的。

本文的贡献可以分为以下三个部分:

• 提出了一种基于信息几何的攻击深度神经网络的新算法。
  该算法可以表征邻域中的多个对抗子空间，并且可以在不同条件下对深度模型进行高成功率的攻击。

• 采用FIM的特征值作为检测对抗性攻击的特征。分析表明，特征值为其特征的分类器对各种最先进的攻击具有鲁棒性。

• 为深度学习漏洞提供了一种新颖的几何解释。
  理论结果证实了该攻击方法的优越性，并作为表征深度学习模型脆弱性的基础。

Fisher信息度量下的对抗攻击

对抗攻击的目标函数

   对抗扰动$\eta$会使得概率$p(y|\mathbf{x}+\mathbf{\eta })$由正确的概率输出变为错误的概率输出，用KL散度度量概率$p(y|x)$的变化情况，则优化目标可以总结为如下形式：
$$\underset{\mathbf{\eta }}{\max }{D}_{KL}(p(y|\mathbf{x})\Vert p(y|\mathbf{x}+\mathbf{\eta }))\text{\hspace{1em}(1)}$$ $$\text{ s.t. }\Vert \mathbf{\eta }{\Vert }_2^2=ϵ$$
假定对抗$||\eta ||$足够小，则可以对似然函数$\log p(y|x+\eta )$进行二阶泰勒展开，会有如下的FIM简单的二阶形式： $$\begin{array}{rl}{D}_{KL}(p(y|\mathbf{x})\Vert p(y|\mathbf{x}+\mathbf{\eta }))& ={\mathbb{E}}_{\mathbf{y}|\mathbf{x}}\left[\log \frac{p(y|\mathbf{x})}{p(y|\mathbf{x}+\mathbf{\eta })}\right]\\ & \approx \frac{1}{2}{\mathbf{\eta }}^T{\mathbf{G}}_{\mathbf{x}}\mathbf{\eta }\end{array}\text{\hspace{1em}(2)}$$
其中，样本$x$的Fisher信息量为 $${\mathbf{G}}_{\mathbf{x}}={\mathbb{E}}_{\mathbf{y}|\mathbf{x}}\left[\left({\nabla }_{\mathbf{x}}\log p(y|\mathbf{x})\right){\left({\nabla }_{\mathbf{x}}\log p(y|\mathbf{x})\right)}^T\right]\text{\hspace{1em}(3)}$$
证明： $$E_{y|x}[\log \frac{p(y|x)}{p(y|x+\eta )}]=E_{y|x}[\log p(y|x)]-E_{y|x}[\log p(y|x+\eta )]\text{\hspace{1em}(4)}$$
其中， $$\log p(y|x+\eta )=\log p(y|x)+{\nabla }_{\mathbf{x}}\log p(y|x)\cdot \eta +\frac{1}{2}{\eta }^T{\nabla }_{\mathbf{x}}^T{\nabla }_{\mathbf{x}}\log p(y|x)\eta +O({\eta }^2)$$
计算${\mathbb{F}}_x^{{}^{\prime }}$如下: $$\begin{array}{rl}{\mathbb{F}}_x^{{}^{\prime }}& ={\mathbb{E}}_{y\sim p(y|x)}\left[{\nabla }_x\log p(y|x){\nabla }_x^T\log p(y|x)\right]\\ & ={\mathbb{E}}_{y\sim p(y|x)}\left[\frac{{\nabla }_{x}p(y|x)}{p(y|x)}\cdot \frac{{\nabla }_x^{T}p(y|x)}{p(y|x)}\right]\\ & ={\mathbb{E}}_{y\sim p(y|x)}\left[\frac{{\nabla }_{x}p(y|x){\nabla }_x^{T}p(y|x)}{p^2(y|x)}\right]\end{array}\text{\hspace{1em}(5.1)}$$ 计算${\mathbb{F}}_x^{{}^{\prime \prime }}$如下: $$\begin{array}{rl}{\mathbb{F}}_x^{{}^{\prime \prime }}& ={\mathbb{E}}_{y\sim p(y|x)}\left[{\nabla }_x^T(\frac{{\nabla }_{x}p(y|x)}{p(y|x)})\right]\\ & ={\mathbb{E}}_{y\sim p(y|x)}\left[{\nabla }_x^T(\frac{{\nabla }_{x}p(y|x)}{p(y|x)})\right]\\ & ={\mathbb{E}}_{y\sim p(y|x)}\left[\frac{({\nabla }_x^T{\nabla }_{x}p(y|x))p(y|x)-{\nabla }_x^{T}p(y|x){\nabla }_{x}p(y|x)}{p^2(y|x)}\right]\end{array}\text{\hspace{1em}(5.2)}$$又容易推导出: $${\mathbb{E}}_{y\sim p(y|x)}[\frac{{\nabla }_x^T{\nabla }_{x}p(y|x)}{p(y|x)}]=0\text{\hspace{1em}(5.3)}$$
从而根据式子$(5.1)$,$(5.2)$,$(5.3)$可知，${\mathbb{F}}_x^{{}^{\prime }}={\mathbb{F}}_x^{{}^{\prime \prime }}$所以有: $${\mathbb{E}}_{y\sim p(y|x)}[{\nabla }_{\mathbf{x}}^T{\nabla }_{\mathbf{x}}\log p(y|x)]=-{\mathbb{E}}_{y\sim p(y|x)}[{\nabla }_{\mathbf{x}}\log p(y|x){\nabla }_{\mathbf{x}}^T\log p(y|x)]\text{\hspace{1em}(6)}$$
综上， $$\begin{array}{rl}{\mathbb{E}}_{\mathbf{y}|\mathbf{x}}\left[\log \frac{p(y|\mathbf{x})}{p(y|\mathbf{x}+\mathbf{\eta })}\right]& =-{\mathbb{E}}_{y|x}[{\nabla }_{\mathbf{x}}\log p(y|x)\cdot \eta ]+\frac{1}{2}{\eta }^T{G}_x\eta +O({\eta }^2)\\ & \approx \frac{1}{2}{\eta }^T{G}_x\eta \end{array}\text{\hspace{1em}(7)}$$
其中， $${\mathbf{G}}_{\mathbf{x}}={\mathbb{E}}_{y|x}[{\nabla }_{\mathbf{x}}\log p(y|x){\nabla }_{\mathbf{x}}^T\log p(y|x)]\text{\hspace{1em}(8)}$$
证毕。
样本$x$的Fisher信息量的离散形式表示为： $${\mathbf{G}}_{\mathbf{x}}=\sum _i{p}_i\left[{\nabla }_{\mathbf{x}}\mathcal{J}\left(y_i,\mathbf{x}\right)\right]{\left[{\nabla }_{\mathbf{x}}\mathcal{J}\left(y_i,\mathbf{x}\right)\right]}^T\text{\hspace{1em}(9)}$$
其中，$\mathcal{J}(y,\mathbf{x})=-\log p(y|\mathbf{x})$表示得是样本$x$为第$y$类的损失函数。综上，会得到目标函数的变体如下所示：$$\underset{\mathbf{\eta }}{\max }{\mathbf{\eta }}^T{\mathbf{G}}_{\mathbf{x}}\mathbf{\eta }\text{ s.t. }\Vert \mathbf{\eta }{\Vert }_2^2=ϵ,\mathcal{J}(y,\mathbf{x}+\mathbf{\eta })>\mathcal{J}(y,\mathbf{x})\text{\hspace{1em}(10)}$$
可知，此函数的拉格朗日函数为如下形式： $$L(\eta ,\lambda )={\eta }^T{G}_x\eta -\lambda {\eta }^T\eta \text{\hspace{1em}(11)}$$
对拉格朗日求导可得： $$\frac{\partial L(\eta ,\lambda )}{\partial \eta }=0\text{\hspace{1em}(12)}$$ 求解为：
$$2G_x\eta -2\lambda \eta =0\text{\hspace{1em}(13)}$$ 化简可得： $$G_x\eta =\lambda \eta \text{\hspace{1em}(14)}$$ 进一步可以得出 $$max\{{\eta }^T{G}_x\eta \}={\lambda }_{max}{\eta }^T\eta ={\lambda }_{max}\cdot \epsilon \text{\hspace{1em}(15)}$$
至此，可以将对优化问题的求解可以看成是对矩阵$G_x$进行特征分解并求其最大特征值${\lambda }_{max}$的过程，此时最大特征值${\lambda }_{max}$对应的特征向量$\eta$即为所求。另外需要加入$\mathcal{J}(y,\mathbf{x}+\mathbf{\eta })>\mathcal{J}(y,\mathbf{x})$的约束条件保证对抗样本的损失函数要比干净样本的损失函数要大，即保证对抗样本的对抗性。这个方法的重要意义是当考虑到$D_{KL}(p(y|\mathbf{x})\Vert p(y|\mathbf{x}+\mathbf{\eta }))$为对抗扰动$\eta$的函数时，则Fisher信息矩阵是KL散度的Hessian矩阵。这意味着深度模型的脆弱性可以由KL散度的曲率来描述。对定一个样本$x$，Fisher信息矩阵的特征值表征了对应特征向量的子空间的鲁棒性。特征值越大，深度模型越脆弱。

优化策略

  在大数据集下，如果直接特征分解矩阵$G_x$的最大的特征向量，那么计算复杂度会非常大。为了避免计算开销可以通过计算${\mathbf{G}}_{\mathbf{x}}\mathbf{\eta }$来代替。则会有如下形式：
$${\mathbf{G}}_{\mathbf{x}}\mathbf{\eta }={\mathbb{E}}_{y|\mathbf{x}}\left[\left({\mathbf{g}}_y^T\mathbf{\eta }\right){\mathbf{g}}_y\right]\text{\hspace{1em}(19)}$$
其中，${\mathbf{g}}_y={\nabla }_{\mathbf{x}}\mathcal{J}(y,\mathbf{x})$是类$y$的损失函数关于样本$x$的梯度。此方法是通过计算内积来代替处理矩阵的特征分解，其中，最大的特征值为${\mathbb{E}}_{y|\mathbf{x}}\left[{\left({\mathbf{g}}_y^T\mathbf{\eta }\right)}^2\right]$。用幂迭代的方法来加速矩阵$G_x$的特征分解，具体的迭代形式如下所示：
$${\mathbf{\eta }}_{k+1}=\frac{{\mathbb{E}}_{y|\mathbf{x}}\left[\left({\mathbf{g}}_y^T{\mathbf{\eta }}_k\right){\mathbf{g}}_y\right]}{\Vert {\mathbb{E}}_{y|\mathbf{x}}\left[\left({\mathbf{g}}_y^T{\mathbf{\eta }}_k\right){\mathbf{g}}_y\right]\Vert }\text{\hspace{1em}(20)}$$相似的方法可以用来计算前$m$个大的特征值和与之对应的特征向量。计算矩阵$G_x$的另一个难点在于求和计算需要依赖于分布$p(y|x)$，但是模拟一个类别很大的数据集的分布会比较困难。在实际中，对分布$p(y|x)$进行蒙特卡洛模拟来进而对积分进行近似求解。采样的数量是大约是类别的$\frac{1}{5}$，但是模拟估计的数值依旧准确。随机采样用到的方法是alias方法。具体的算法如下所示：

  OSSA算法在MNIST， CIFAR-10，ILSVRC-2012数据集上生成的对抗样本的可视化如下图所示：

几何解释

  研究对抗性样本的一个重要问题就是表征神经网络的脆弱性。在欧式度量下已经表明识别RELU网络中最坏对抗扰动是一个NP-hard问题。本论文从另一个不同的方面来解释深度学习的脆弱性，即在Fisher信息量度标准下，通过OSSA算法获得的对抗扰动不会经过神经网络而映射压缩掉，这导致了深度学习的脆弱性。其中，在不需要假设任何网络结构条件下由OSSA算法获得最优性对抗扰动的理论基础可以解释为过度线性解释的推广。这说明由Goodfellow(2014)提出的过度线性化的理论可能不是神经网络脆弱性的充分条件，并且使用OSSA算法可以在具有平滑激活的网络中再现对抗攻击，例如指数线性单位。

实验结果

白盒攻击算法性能比较

  本实验比较OSSA，FGM，OTCM这三种攻击算法的攻击模型的能力。如下图(a)所示，在单步攻击下，模型误分类率随着扰动大小的增加而增大，并且可知OSSA攻击算法在给定一个扰动下，它会以更快的速度达到一个高的攻击准确率。如下图(b)所示，在多步迭代攻击中，模型误分类率随着攻击的迭代次数的的增加而增大，并且可知OSSA算法在给定一个扰动下，能更快的收敛到一个较高的攻击准确率。

黑盒攻击迁移性探究

  本实验是探究由OSSA算法生成对抗样本在不同模型(尤其是通过对抗训练正则化的模型)中迁移性的情况，该实验是在MNIST上进行的，该网络具有四个不同的网络：LeNet，VGG及其对抗训练变体，在这里分别称为LeNet-adv和VGG-adv。实验结果如下表所示，对抗样本跨模型的迁移率在不同模型之间是不对称的，未经对抗训练的模型迁移到经过对抗训练的模型平均会产生22.51％的误分类率，而反之平均产生80.52％的误分类率。

表征多重对抗子空间

  Fisher信息度量可以用于测量模型局部鲁棒性，因此本实验来验证模型鲁棒性与Fisher信息矩阵的最大特征值之间的关系。如下图所示，显示了MNIST和CIFAR-10的验证集中的800个随机选择的样本的分散性，。横轴是特征值的对数，而纵轴是最小的对抗扰动大小。结果表明，特征值与模型易损性之间存在明显的相关性：最小扰动随特征值的指数增长线性减小。合理的解释是，特征值反映了Fisher信息量度下的扰动大小。根据最优性分析，较大的特征值会导致输出似然性的等距变化，从而更有可能以较小的扰动大小欺骗模型。

Fisher信息度量的对抗检测

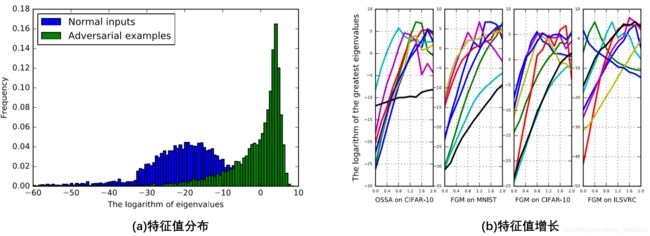
  本实验探究Fisher信息矩阵中的特征值是如何检测对抗攻击。如下图所示，图(a)显示了特征值分布的直方图，FGM为MNIST的样本生成对抗样本，并在FIM中评估其最大特征值。直方图显示正常样本和对抗样本的特征值分布大小不同。后者的特征值在较大的域中密集分布，而前者的分布近似为具有较小均值的高斯分布，但是通过添加更多特征值作为特征，可以大大增强对抗示例的可分离性。图(b)为特征值随扰动大小的增加而大，这表明与正常样本相比，对抗样本在Fisher信息矩阵中具有更高的特征值。

总结交流

  本文研究了基于信息几何的对抗攻击与检测，提出了一种将对抗性攻击与检测相结合的方法。对于攻击，本文证明了在Fisher信息度量下，最优对抗扰动是输入空间和输出空间之间的等距，这可以通过求解FIM的一个约束二次型得到。对于检测，Fisher信息矩阵的特征值能够很好地描述模型的局部脆弱性。这种特性能够建立机器学习分类器来检测具有特征值的对抗性攻击。实验结果表明，以特征值为特征的分类器对各种最新攻击的检测具有很好的鲁棒性。解决对抗性攻击问题通常是困难的。其中一个巨大的挑战是缺乏描述和分析深度学习模型的理论工具。黎曼几何学是一种很有前途的方法，可以更好地理解深度学习的脆弱性。
在本文中主要关注的是分类任务，其中模型的似然估计是离散分布。除了分类之外，还有许多其他的任务可以表示为统计问题，例如回归任务的高斯分布。因此，研究其他任务的对抗性攻击和防御将是一个有趣的未来方向。