python 之 numpy 模块详细讲解及其应用案例

python numpy 模块详细讲解及应用案例

博文简介

• 该博文总共介绍3个常用的numpy方法（array，linspace，arange），同时每个方法都会有一个应用举例，通过应用举例来更好地理解和使用这些方法
• 当然numpy还有一些数学上的操作方法，这个就是最熟悉的:
  sin(), cos(), log(),tan(),exp(),arctan(),arcsin(),arccos(),cot()等等
  大家懂得数学就一定会那些方法了，故在这里就不做介绍了

一、安装numpy

windows 系统：
1.windows + R 打开控制台;
2.pip install numpy。
结果如下所示：

二、最常用的方法

1、array方法

1.1 array（numpy.array）功能
生成数组（可以是一维数组，二维数组，甚至更高维度的数组）
数组与列表的区别：
数组必须是同样的数据类型；
而列表可以是不同数据类型。
在其他方面二者相差无几。
举例：

import numpy as np
"""
业界最通用的操作，声明一个别名np
"""
array_0 = np.array([0, 1, 2, 3, 4])
# 一维数组
array_1 = np.array([[0, 1, 2, 3],[4, 5, 6, 7]])
# 二维数组
array_2 = np.array([[[0, 1, 2],[3, 4, 5]],[[6, 7, 8],[9, 10, 11]]])
# 三维数组
# 更多维度的几乎不会使用到的
"""
这里注意：
数组必须是同一个数据类型的元素构成，
所以，当元素的数据类型不同时，
会发生强制准换！！
准换的优先级为：
字符串 > 浮点数 > 整型数
例如下面的举例：
"""
array_3 = np.array([1, 2.23, 4, 5])
# 会强制转换为浮点数
array_4 = np.array([1, 2.23, 4, 5, 'hello world !'])
# 会强制转换为字符串

# 打印结果
print(array_0)
print(array_1)
print(array_2)
print(array_3)
print(array_4)

运行的结果如下所示（output）：

[0 1 2 3 4]
# array_0

[[0 1 2 3]
 [4 5 6 7]]
# array_1
 
[[[ 0  1  2]
  [ 3  4  5]]

 [[ 6  7  8]
  [ 9 10 11]]]
# array_2

[1.   2.23 4.   5.  ]
# array_3

['1' '2.23' '4' '5' 'hello world !']
# array_4

总之就是说，numpy.array()是来生成数组的，其类型为：
（可以通过type（）方法来查看）。
另外，一个数组减去一个数字，例如：

array_0 = array_0 - 100
# 每个元素都减一百

意味着数组中的每一个元素都要减去100！
1.2 array方法的应用举例（可以处理图片）

import numpy as np
import matplotlib.pyplot as plt
# 这是一个绘图专用的模块，该模块的介绍将在另一篇博文中进行讲述
"""
同样是业界常用别称
"""

# 将图片转换为一个数组（三维数组）
array_img = plt.imread('./图片名称')
"""
例如：
array_img = plt.imread('./0065ErDtgy1geehlwnfb6j30p018g435.jpg')
"""
# 相当于是要输入一个图片文件的位置
# 得到的结果是一个三维数组
# 通过print查看
print(array_img)
# print(type(array_img))


# 利用绘图模块展示出来
plt.imshow(array_img)
# 实现一个数组减去一个数字：
plt.imshow(array_img - 100)
# 加一个数字也可以
plt.imshow(array_img + 200)

运行的结果如下所示（output）：
这里我是已经用了一张图片的， 原图如下，运行的效果请参见下方的下方：

此处展示图片：
1、对应于 array_img ： (没有变化)

2、对应于 array_img - 100 ：（把可爱的小姐姐变丑了，是我的过错，呜呜呜~~~）

3、对应于 array_img + 200 ：（又一次把小姐姐变丑了，呜呜呜~~~，先说声对不起~~，但似乎比前一个好一点啦~）

所以呢，其实那些修图软件就是将拍摄后的图片转换成为数组，然后通过特定的算法来实现美颜、瘦身等功能的。
比如：
对于常用的瘦脸功能，我们可以：
1、拍照；
2、识别人脸；
3、将整个图片转成数组；
4、利用特定的算法来处理人脸所对应的数组区域；
5、最后，显示处理后的图片（即，经过瘦脸后的图片）。
（在这里就不去实现这种复杂的功能了，有兴趣的大佬可以自己探索一下哦~）

2、linspace方法

2.1 linspace 方法的功能
linspace 方法的功能是产生一个一维数组，具体实现是将从起始位置开始到结束位置为止的区间，均匀地产生指定个数的数字，并将这些数字组成一个一维数组。

import numpy as np
array_0 = np.linspace(-10, 20, 30)
# 第一个参数：起始位置
# 第二个参数：结束为止
# 第三个参数：产生的一维数组的大小，即指定的数字个数
print(array_0)

输出结果：（相当于等差数列！！）

[-10.          -8.96551724  -7.93103448  -6.89655172  -5.86206897
  -4.82758621  -3.79310345  -2.75862069  -1.72413793  -0.68965517
   0.34482759   1.37931034   2.4137931    3.44827586   4.48275862
   5.51724138   6.55172414   7.5862069    8.62068966   9.65517241
  10.68965517  11.72413793  12.75862069  13.79310345  14.82758621
  15.86206897  16.89655172  17.93103448  18.96551724  20.        ]

（共有30个数字）
2.2 linspace 方法的应用举例
在这里举一个绘制图像的例子，绘制一个三维曲线

"""
绘制一个三维的曲线
所绘制的曲线为等距螺旋线
等距螺旋线绘制代码以及结果如下：
"""
import numpy as np
import matplotlib.pyplot as plt
# 导入库函数
fig = plt.figure()
# 建立一个三维坐标系
ax1 = plt.axes(projection='3d')
# 进行三维绘图
z = np.linspace(-5, 5, 50)
# 使用 linspace 方法定义z坐标
"""
从-5到5的区间，均分为50份进行描点绘图
描点！！
"""
x = 5 * np.sin(z)
y = 5 * np.cos(z)
# 定义x与y的坐标
ax1.plot3D(x, y, z, 'gray')
# 实现三维图的绘制
plt.show()
# 显示绘制的图像结果

结果展示如下所示：

以上便是linspace方法的一个简单介绍。

3、 arange方法

3.1 arange 方法的功能
产生一个从初始位置开始，到终止位置结束，以特定步长为差值的以为数组（也相当于等差数列）：

import numpy as np
array_0 = np.arange(-10, 10, 2)
# 使用arange方法
# 第一个参数：起始位置
# 第二个参数：终止位置
# 第三个参数：步长

# 打印
print(array_0)

运行结果如下所示：

[-10  -8  -6  -4  -2   0   2   4   6   8]

3.2 arange 方法的应用举例
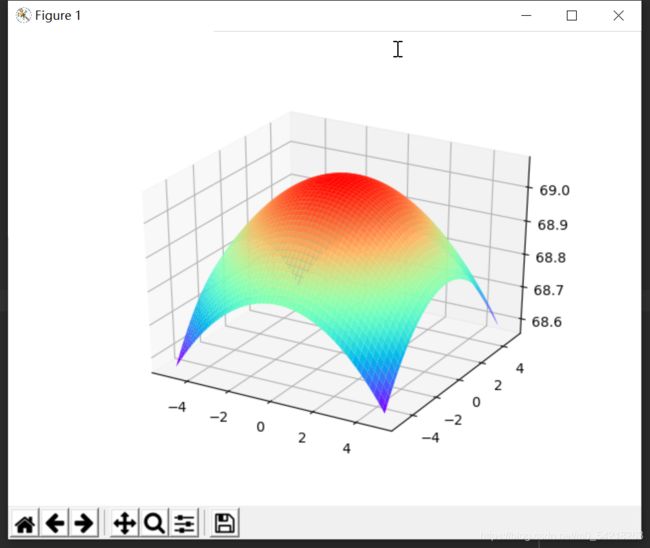
在这里我们绘制一张三维空间中的一个曲面图像，具体的代码实现如下：

"""
前四行代码与上一个例子相同！！
"""
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax3 = plt.axes(projection='3d')
# 定义x坐标--->生成数组
x = np.arange(-5, 5, 0.1)
# 定义y坐标--->生成数组
y = np.arange(-5, 5, 0.1)

# 在这里，生成一个二维的数组来存放坐标（二维坐标的存放 ！！）
# （meshgrid是另一个方法，在这里不多介绍，有兴趣可以查阅相关资料来学习。）
X, Y = np.meshgrid(x, y)
# Z 的函数关系式
Z = 10 * np.log(1000 - X ** 2 - Y ** 2)

# 显示图像，cmap参数是设置图形的样式的，rainbow为彩虹状
ax3.plot_surface(X, Y, Z, cmap='rainbow')
# 别忘了plt.show()!!
plt.show()

运行结果展示如下所示：

总结

综上所述：
numpy（np） 模块 的这三种方法就介绍到这里了啦~~~

当然以上介绍是不够的全面的，想要真正掌握这些模块，还是应该自己多练习、多实践，以此来增强自己的技能，此篇仅供大家参考所用~
要是喜欢的话可以点一个赞（么么哒），当然要是不喜欢的话也希望不要踩一下啦~