python列表与链表用处_浅谈Python的列表和链表

本文从实现原理的角度比较了python的列表和链表的性能差异, 并且通过LRU算法,实现一个最大堆等实例来阐明如何正确地使用它们.

一. 从归并排序说起

归并排序是分治法的一个经典实现案例, 我特别喜欢. 在维基百科里面, 使用python实现的归并排序实例如下:

defmergeSort(nums):if len(nums) < 2:returnnums

mid= len(nums) // 2left=mergeSort(nums[:mid])

right=mergeSort(nums[mid:])

result=[]while left andright:if left[0] <=right[0]:

result.append(left.pop(0))else:

result.append(right.pop(0))ifleft:

result+=leftifright:

result+=rightreturnresult

但是, 这个案例存在性能问题.现在, 我们重写一个归并排序函数, 然后测试二者的性能:

def myMergeSort(nums: [int]) ->[int]:#我们重写的归并排序算法

if len(nums) < 2:returnnums

mid= len(nums) // 2left=myMergeSort(nums[:mid])

right=myMergeSort(nums[mid:])

m, n=0, 0for i inrange(len(nums)):if n >= len(right) or (m < len(left) and left[m]

nums[i]=left[m]

m+= 1

else:

nums[i]=right[n]

n+= 1

returnnumsdef test(func: Callable[[List[int]], List[int]]) ->None:

li= list(range(int(1e5)))

ans=li[:]

random.shuffle(li)

start=time.time()assert func(li) ==ansprint('func: {}, time cost: {:.2f}s'.format(func.__name__, time.time() -start))if __name__ == '__main__':

test(mergeSort)

test(myMergeSort)

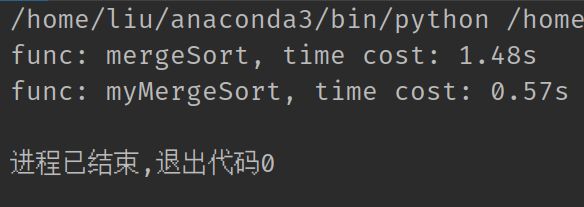
二者的执行用时如下:

可以看到, 我们写的归并函数明显性能更好, 这主要是由于, 我们在合并left和right两个列表时, 使用的是移动指针而非pop(0)操作, 后者的时间复杂度是O(n), 这直接把一个时间复杂度O(n log n)的算法优化到O(n³ log n).

二. 列表和链表的实现原理

1. 列表的储存原理

列表是在CPython的C层面实现的, 其本质上是一个数组, 数组的值为列表对应位置元素的指针. 对于一个数组来说, 它占有连续的内存空间:

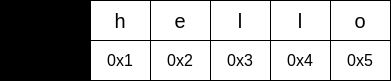
因此, 假如我们现在有一个python列表, 其值为['h', 'e', 'l', 'l', 'o'], 那么在内存空间中, 它大概是长这个样子的:

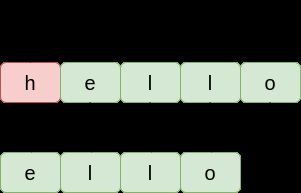
这样做的好处是便于寻址, 由于内存地址连续, 我们可以在常数级别的时间内获取到位置为i的元素. 但是, 假如我们要添加或者删除元素, 情况就不一样了. 比如对于刚才的数组, 我们执行pop(0)操作:

对于列表而言, 向i位置添加或删除一个元素, 在i之后的所有元素都要挪动位置. 这也就解答了上一章提出的问题: 为什么列表pop(0)的时间复杂度为O(n).

2. 列表的扩容机制

上一节讲到, python列表的底层实现是一个数组, 数组的值指向对应位置元素的指针. 但是, 数组的长度是固定的, 添加或删除元素很不方便. 为了应对这个问题, python使用扩容机制对列表进行了优化. 下面的代码展示了python的扩容机制:

from sys importgetsizeof

li=[]for _ in range(10):

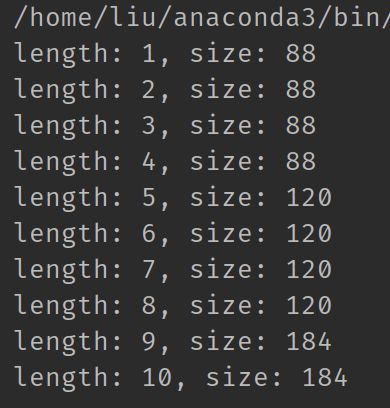
li.append(None)print(f'length: {len(li)}, size: {getsizeof(li)}')

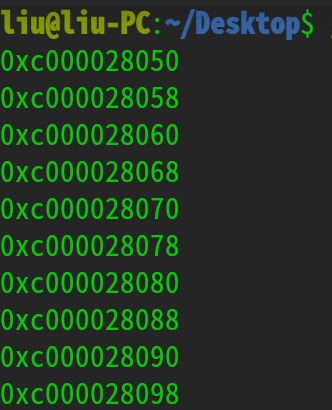
运行结果如下:

可以看到, 列表占用的内存并不是线性增长的. 以['h', 'e', 'l', 'l', 'o']这个数组为例, 它在底层长这样:

对于一个列表, CPython为其分配长度为4,8,16,25,35...的数组. 比如上面的这个列表长度为5, 那么其底层数组的长度为8. 这样做的好处是, 在调用append操作时, 如果数组还有闲置空间, 我们就不需要重新创建数组, 等列表长度超过8之后, 我们再创建一个长度为16的数组也不迟. 因此, 虽然数组扩容的时间复杂度为O(n), 但是python避免了频繁的扩容. 把开销分摊到每一次的append上, 时间复杂度就是O(1).

pop(-1)的机制同理, python不会频繁地缩减空间, 因此时间复杂度也是O(1).

3. 链表的实现原理

通过如下代码, 我们就能定义一个链表:

classLinkNode:def __init__(self, val: int = 0) ->None:

self.val=val

self.next=Nonedef __repr__(self) ->str:#别这么用,链表过长会超过递归层数

return f'{self.val}->{repr(self.next)}'@staticmethoddef make(arr: [int]) -> Optional['LinkNode']:

root=LinkNode()

node=rootfor num inarr:

node.next=LinkNode(num)

node=node.nextreturnroot.next

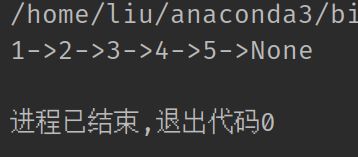
link= LinkNode.make([1, 2, 3, 4, 5])print(link)

运行结果如下:

如果没有特殊需求, 建议使用collections库中自带的deque链表, deque的文档

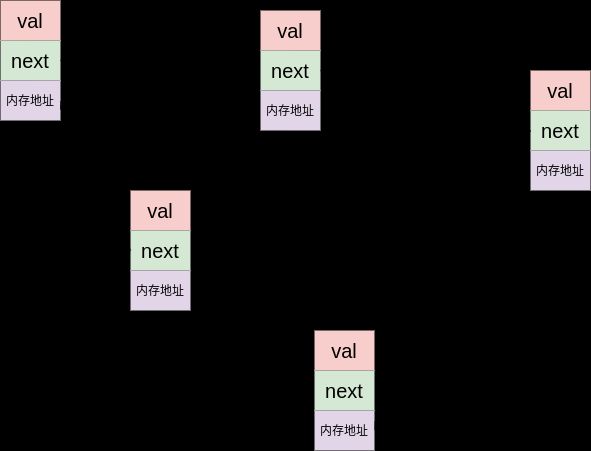
链表的最大特点是内存不连续, 每个节点储存着下一个节点的指针. 在内存中它大概长这样:

相对于列表来说, 链表不能迅速定位元素, 如果你想要找到一个节点, 你就首先得找到这个节点的上一个节点, 要找到上一个节点, 你就得找到上一个节点的上一个节点. 循环往复, 直到头节点为止.

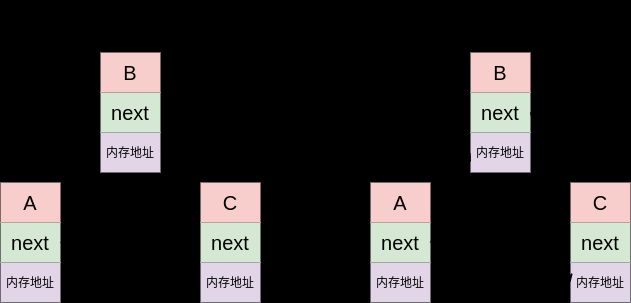
但是, 链表的这种数据结构也带来了插入和删除元素上的优势, 比如我们已经得到了A节点, 现在要在A节点之后插入B:

在上面的例子中, 我们只需要让A节点重新指向B, 然后让B指向C, 这样就完成了插入. 由于每个节点都只和它之前的一个节点有关联, 因此插入和删除节点的时间复杂度都是O(1).

4. 二者的性能对比和总结

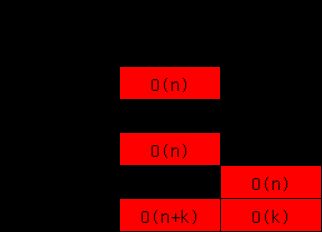
总的来说, 列表和链表的最大区别是前者的内存空间连续, 后者不连续. 因此列表寻址很快, 插入和删除数据慢, 而链表相反, 对于python自带的deque双向链表来说, 头尾部的插入和删除很快, 索引很慢. 二者常用操作的时间复杂度如下:

三. 一些应用实例

1. LRU算法

LRU即Least Recently Used, 翻译成中文就是最近最少使用. 简单点说, 假如我们有一摞书:

现在要看某一本的话, 就会把它抽出来, 看完后, 再放回这摞书的最顶端. 这样, 近期看得最少的书很难获得放在最顶端的机会, 它就会一直在最底端. 等书的数量增多, 书架放不下之后, 最底端的肯定是最不常看的, 我们就可以把它扔掉, 这就是LRU算法.

现在我们用python来实现这样一个数据结构: 它提供get和set两个接口, 当调用set时, 如果容量达到上限, 它会基于LRU算法删除不常用的数据:

classLRUCache:def __init__(self, capacity: int) ->None:

...def get(self, key: int) ->int:

...def set(self, key: int, value: int) ->None:

...

首先, 基于上面对LRU算法的分析, 我们可以用一个链表来存放数据, 当一个节点被外部访问时, 我们就把它移动到链表头部, 当容量达到上限时, 我们就把链表尾部的节点移除. 由于链表的特性, 上述这些操作的时间复杂度都是O(1).

LRU淘汰算法解决了, 下一个问题就是如何定位到节点. 理论上, 定位到链表节点需要的时间复杂度为O(n), 这显然是无法接受的. 一个常用的优化方式就是用一个哈希表储存所有的节点地址, 这样我们就可以在O(1)的时间内定位到任意节点.

基于以上的分析, 我们使用一个双向链表和一个哈希表来实现LRU算法, 其get和set操作的时间复杂度都是O(1):

classLinkNode:def __init__(self, key: int = 0, value: int = 0) ->None:

self.key=key

self.value=value#为了更方便,这里使用双向链表,两个指针分别指向前置节点和后置节点

self.prev =None

self.next=Nonedef connect(self, node: 'LinkNode') ->None:

self.next=node

node.prev=selfclassLRUCache:def __init__(self, capacity: int) ->None:

self.capacity=capacity

self.size=0#所有的节点都储存在头部和尾部之间

self.head =LinkNode()

self.tail=LinkNode()

self.head.connect(self.tail)#用一个字典来快速定位节点

self.nodes ={}def get(self, key: int) ->int:if key not inself.nodes.keys():return -1node=self.nodes[key]

self.add_to_head(node)returnnode.valuedef set(self, key: int, value: int) ->None:if key inself.nodes.keys():

self.nodes[key].value=valueelse:

self.nodes[key]=LinkNode(key, value)

self.size+= 1

if self.size >self.capacity:

last=self.tail.prevdelself.nodes[last.key]

last.prev.connect(self.tail)

self.add_to_head(self.nodes[key])def add_to_head(self, node: LinkNode) ->None:if node.prev andnode.next:

node.prev.connect(node.next)

node.connect(self.head.next)

self.head.connect(node)

此外, python的有序字典OrderedDict内部就是用一个双向链表来保持有序的, 因此我们也可以直接用它来实现LRU算法:

classLRU(OrderedDict):'Limit size, evicting the least recently looked-up key when full'

def __init__(self, maxsize=128, /, *args, **kwds):

self.maxsize=maxsize

super().__init__(*args, **kwds)def __getitem__(self, key):

value= super().__getitem__(key)

self.move_to_end(key)returnvaluedef __setitem__(self, key, value):if key inself:

self.move_to_end(key)

super().__setitem__(key, value)if len(self) >self.maxsize:

oldest=next(iter(self))del self[oldest]

2. 实现一个最大堆

这个内容有点多, 我单独写了一篇文章-> 用Python实现最大堆.

3. 列表当成字典用

python字典的本质是一个哈希表, 其具体实现原理可以看这篇文章. 考虑到哈希冲突, 字典取值可能需要额外时间. 而相对的, 列表寻址很快, 而且每个索引值(不考虑负值)都指向列表中独一无二的位置. 现在我们分别测试二者的性能:

importrandomimporttimeimportsys

n= 10000

#长度为n的字典, key值在[0, n - 1]之间, value为a-z的某个字母

dict = {k: chr(random.randrange(97, 123)) for k inrange(n)}#用列表来存放dic的所有信息

list = [None] * 10000

for k, v indict.items():

list[k]=vdeftest(data):print(type(data))print(f'size:{sys.getsizeof(data)}')

start=time.time()for _ in range(100):for key inrange(n):

value=data[key]print('time cost: {:.5f}s'.format(time.time() -start))

test(dict)

test(list)

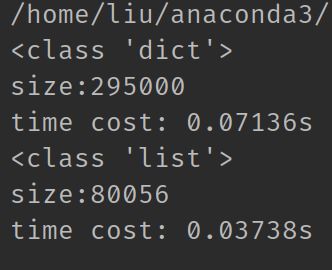
程序运行结果如下:

可以看到, 不管是内存占用还是取值需要时间, 列表都完胜字典.

基于以上, 在key值都是自然数的前提下, 列表是可以代替字典的, 其取值速度和内存占用都优于字典. 但是, 如果数据经常发生添加和删除等变动, 这时候列表就不占性能优势了. 因此, 是否用列表代替字典, 还得根据实际场景来定.

4. 小结

1. 链表的寻址很慢, 为了弥补这一劣势, 我们可以根据实际情况使用哈希表映射到链表节点, 降低寻址的时间复杂度;

2. 列表的索引机制给了它无限的可能, 它可以当二叉树用, 可以当字典用. 然而, 这些用法都有明显的局限性, 实际项目中还是得具体问题具体分析.