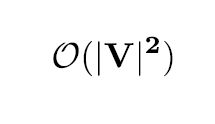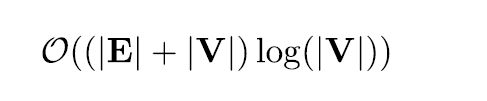运动规划（Motion planning）-Dijkstra算法

Hello,朋友们。第二篇博客我们还是接着聊运动规划算法。

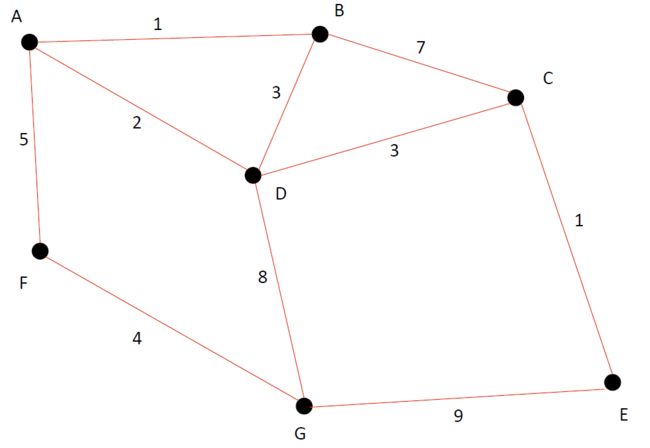
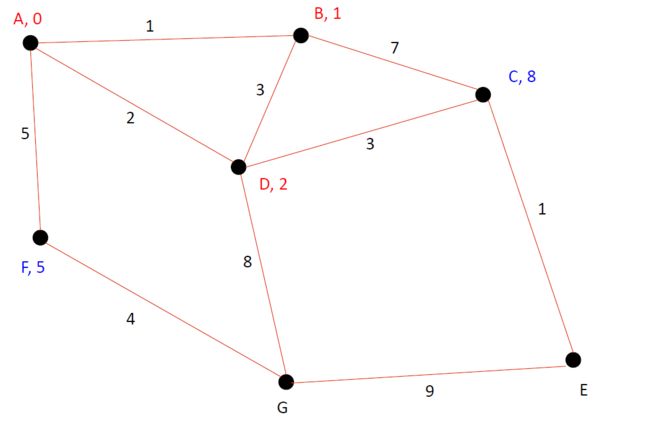
上图，图中字母表示不同的地点，数字表示两点之间的距离。我们要找到图中的最短路径，就拿A到E点做例子好了。

图1

我们的目标是：找到start-end之间的最短路径，如图所示

图2

来吧，Dijkstra-迪杰斯特拉算法，这是一种基于贪心策略的动态规划算法（后面解释这句话），可以用来解决最短路径问题。

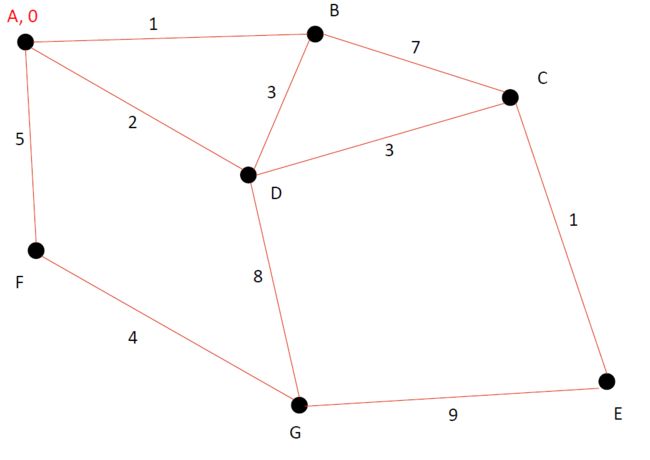
首先把起点的距离设定为0（A到A当然是0距离拉），然后把已经确认该点到起点之间的距离为最短距离的点标红（血统清晰）

图3

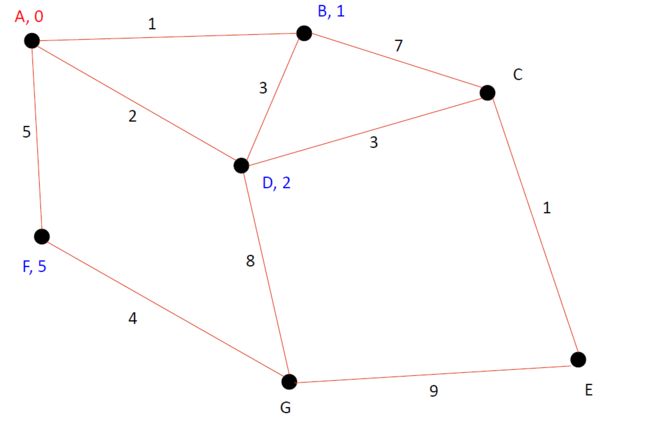
下一步，我们考虑和A相邻的点B，D， F ，把这些候选者们标蓝（血统不明）

图4

很快我们就确定了A-B之间的最短距离为1，然后呢我们考虑B的相邻下一站C。虽然A-C之间有3条路，A-B-C，A-D-C，A-B-D-C，但是目前我们只确定了A-B之间的最短距离，所以暂定A-C之间的距离为8

image.png

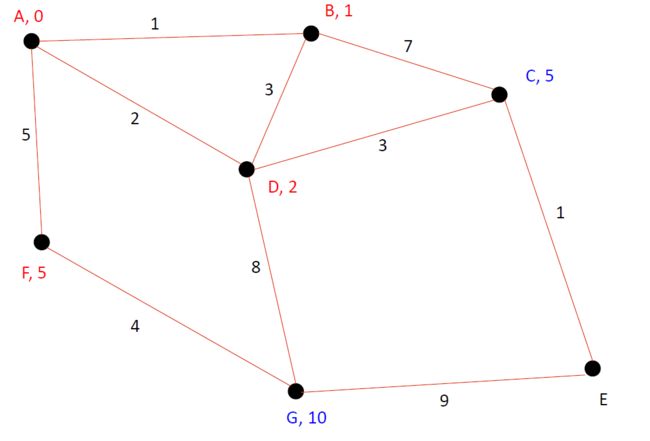
接下里，我们确认A-D最短距离为2。这时候A-C之间的已知的最短距离更新了，为5。感觉越来越接近真相了哈。

图5

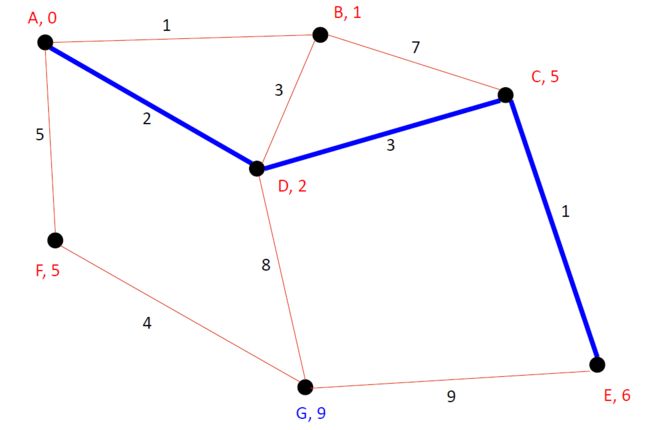
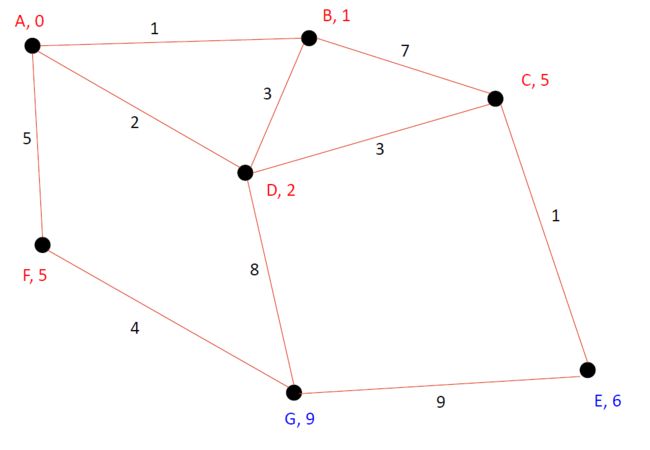
接下来我们再确定了G点和E点后

图6

我们最终确认A-E之间的最短距离为6，我们得到了我们的目标图。

图7

总结一下，事实总是逐渐揭露的，追随着永恒的脚步，我独自走在深蓝的的路上说的就是这种算法。

整个过程用伪代码表示就是：

image.png

这个算法计算复杂度的问题，从伪代码中我们可以看出，实现需要两层循环，第一层循环遍历所有的结点，第二层循环遍历每个节点周围的路径，所以，比较朴实的实现方法的话，计算复杂度为：

image.png

如果我们事先用优先队列PriorityQueue对节点进行排序，可以降低计算复杂度：

image.png

其中，V是图中节点的数量，E为路径条数。

一般意义上的贪心算法在对问题求解时，总是做出在当前看来是最好的选择，也就是做出局部最优解。迪杰斯特拉算法只考虑每个节点的最短路径，然后从中再考虑到达相邻节点的最短路径，这符合了贪心策略。同时待求解的问题分解为若干个子问题，前一子问题的解，为后一子问题的求解提供了有用的信息这又符合了动态规划的选择。所以迪杰斯特拉算法是基于贪心策略的动态规划算法，最后求出一定是整体最优解。

下面附上python代码：

from collections import defaultdict
class Graph:
  def __init__(self):
    self.nodes = set()
    self.edges = defaultdict(list)
    self.distances = {}

  def add_node(self, value):
    self.nodes.add(value)

  def add_edge(self, from_node, to_node, distance):
    self.edges[from_node].append(to_node)
    self.edges[to_node].append(from_node)
    self.distances[(from_node, to_node)] = distance
    self.distances[(to_node, from_node)] = distance


def dijsktra(graph, initial):
  visited = {initial: 0}
  path = {}

  nodes = set(graph.nodes)

  while nodes:
    min_node = None
    for node in nodes:
      if node in visited:
        if min_node is None:
          min_node = node
        elif visited[node] < visited[min_node]:
          min_node = node

    if min_node is None:
      break

    nodes.remove(min_node)
    current_weight = visited[min_node]

    for edge in graph.edges[min_node]:
      weight = current_weight + graph.distances[(min_node, edge)]
      if edge not in visited or weight < visited[edge]:
        visited[edge] = weight
        path[edge] = min_node

  return visited, path

g = Graph()

g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_node('D')
g.add_node('E')
g.add_node('F')
g.add_node('G')

g.add_edge('A','B',1)
g.add_edge('A','D',2)
g.add_edge('A','F',5)
g.add_edge('B','D',3)
g.add_edge('B','C',7)
g.add_edge('D','C',3)
g.add_edge('D','G',8)
g.add_edge('C','E',1)
g.add_edge('G','E',9)
g.add_edge('F','G',4)


print(dijsktra(g, 'E'))

({'E': 0, 'C': 1, 'G': 9, 'B': 7, 'D': 4, 'A': 6, 'F': 11}, {'C': 'E', 'G': 'E', 'B': 'D', 'D': 'C', 'A': 'D', 'F': 'A'})

另附github上很洋气的解法：

from collections import defaultdict
from heapq import *

def dijkstra(edges, f, t):
    g = defaultdict(list)
    for l,r,c in edges:
        g[l].append((c,r))

    q, seen = [(0,f,())], set()
    while q:
        (cost,v1,path) = heappop(q)
        if v1 not in seen:
            seen.add(v1)
            path = (v1, path)
            if v1 == t: return (cost, path)

            for c, v2 in g.get(v1, ()):
                if v2 not in seen:
                    heappush(q, (cost+c, v2, path))

    return float("inf")

if __name__ == "__main__":
    edges = [
        ('A', 'B', 1),
        ('A', 'D', 2),
        ('A', 'F', 5),
        ('B', 'D', 3),
        ('B', 'C', 7),
        ('D', 'C', 3),
        ('D', 'G', 8),
        ('C', 'E', 1),
        ('G', 'E', 9),
        ('F', 'G', 4)
    ]

    print ("=== Dijkstra ===")
    print (edges)
    print ("A -> E:")
    print (dijkstra(edges, "A", "E"))

=== Dijkstra ===
[('A', 'B', 1), ('A', 'D', 2), ('A', 'F', 5), ('B', 'D', 3), ('B', 'C', 7), ('D', 'C', 3), ('D', 'G', 8), ('C', 'E', 1), ('G', 'E', 9), ('F', 'G', 4)]
A -> E:
(6, ('E', ('C', ('D', ('A', ())))))