IOU,GIOU,DIOU,CIOU

IOU: https://www.jianshu.com/p/e3bf67cd4459

https://blog.csdn.net/leonardohaig/article/details/103394369?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase
IOU的优点：

IOU

IOU可以作为距离，loss=1-IOU。但是当两个物体不相交时无回传梯度。 (缺陷)
IOU对尺度变化具有不变性，即不受两个物体尺度大小的影响。
以A，B两个box重合的情况为例，若boxes1=[[0,0,10,10],[0,0,5,5]],boxes2=[[0,0,10,10],[0,0,5,5]],此时IOU=[1,1]
IOU的缺点：
无法衡量两框是相邻还是甚远
如下图2所示，两种情况下IOU均为0，(a)中两框距离较近，(b)中两框明显距离要远，但是仅从IOU数值上无法判断两者距离较近还是较远（两个物体不相交时无回传梯度）
IOU不能反映两个物体如何重叠（相交方式）。
如下图3所示，两种情况下的IOU均为0.1428，(a)中两框要比(b)中的相交更整齐一些，但是IOU并没有反映出这个特点。

为了解决这个问题,衍生出了GIOU

GIOU是为克服IOU的缺点同时充分利用优点而提出的

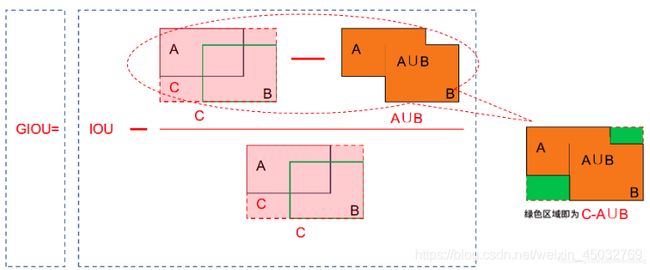
1.假设A为预测框，B为真实框，S是所有框的集合
2.不管A与B是否相交，C是包含A与B的最小框(包含A与B的最小凸闭合框)，C也属于S集合
3.首先计算IoU，A与B的交并比
4.再计算C框中没有A与B的面积，比上C框面积；
5.IoU减去前面算出的比；得到GIoU
6.Note：本文提出的例子中A、B均是矩形框，但是也可以为其他的。比如：A、B为椭圆形，那么此时C将是包含A、B的最小椭圆形；或者A、B均是3D box也可。

论文作者给出几个GIoU的性质：

对尺度的不变性
GIoU可认为是IoU的下界，小于等于IoU
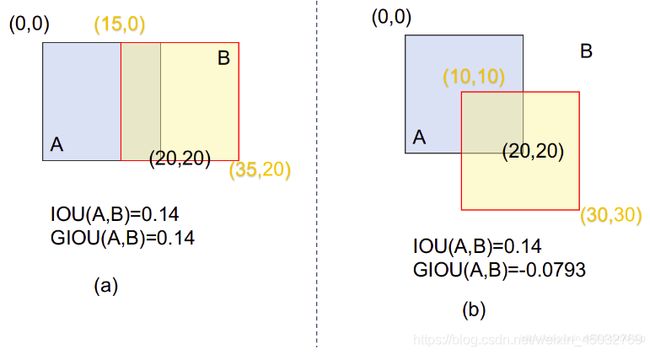
如boxes1=[0,0,10,10],boxes2=[0,0,10,10],此时IOU=1,GIOU=1,这种情况下A与B重合
boxes1=[0,0,10,10],boxes2=[0,10,10,20],此时IOU=0,GIOU=0
boxes1=[0,0,10,10],boxes2=[5,5,15,15],此时IOU=0.1428,GIOU=-0.07936
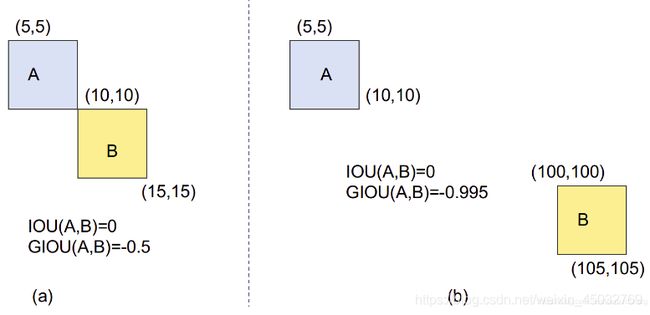
-1<=GIoU<=1，当A=B时，GIoU=IoU=1；当A与B不相交而且离得很远时，GIoU(A,B)趋向于-1。
如boxes1=[[10,10,15,15],[100,100,105,105]],boxes2=[5,5,10,10],计算的GIOU为[-0.5,-0.995],即A与B不相交，随着两者距离增加，GIOU值将趋向于-1，如下图6所示。
因此选用loss=1-GIoU
GIoU能够更好地反应相交情况。如上面图3所示，虽然两种情况下IOU一致，但是(a)中相交的更为整齐，因此GIOU要比(b)中大

GIoU最主要的作用：
(1)对于相交的框，IOU可以被反向传播，即它可以直接用作优化的目标函数。但是非相交的，梯度将会为0，无法优化。此时使用GIoU可以完全避免此问题。所以可以作为目标函数
(2)可以分辨框的对齐方式

目前最适用于损失计算和回归计算的DIOU

DIoU的优点如下：
1.与GIoU loss类似，DIoU loss在与目标框不重叠时，仍然可以为边界框提供移动方向。
2.DIoU loss可以直接最小化两个目标框的距离，而GIOU loss优化的是两个目标框之间的面积，因此比GIoU loss收敛快得多。
3.对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快，而GIoU损失几乎退化为IoU损失

def bboxes_diou(boxes1,boxes2):
    '''
    cal DIOU of two boxes or batch boxes
    :param boxes1:[xmin,ymin,xmax,ymax] or
                [[xmin,ymin,xmax,ymax],[xmin,ymin,xmax,ymax],...]
    :param boxes2:[xmin,ymin,xmax,ymax]
    :return:
    '''

    #cal the box's area of boxes1 and boxess
    boxes1Area = (boxes1[...,2]-boxes1[...,0])*(boxes1[...,3]-boxes1[...,1])
    boxes2Area = (boxes2[..., 2] - boxes2[..., 0]) * (boxes2[..., 3] - boxes2[..., 1])

    #cal Intersection
    left_up = np.maximum(boxes1[...,:2],boxes2[...,:2])
    right_down = np.minimum(boxes1[...,2:],boxes2[...,2:])

    inter_section = np.maximum(right_down-left_up,0.0)
    inter_area = inter_section[...,0] * inter_section[...,1]
    union_area = boxes1Area+boxes2Area-inter_area
    ious = np.maximum(1.0*inter_area/union_area,np.finfo(np.float32).eps)

    #cal outer boxes
    outer_left_up = np.minimum(boxes1[..., :2], boxes2[..., :2])
    outer_right_down = np.maximum(boxes1[..., 2:], boxes2[..., 2:])
    outer = np.maximum(outer_right_down - outer_left_up, 0.0)
    outer_diagonal_line = np.square(outer[...,0]) + np.square(outer[...,1])

    #cal center distance
    boxes1_center = (boxes1[..., :2] +  boxes1[...,2:]) * 0.5
    boxes2_center = (boxes2[..., :2] +  boxes2[...,2:]) * 0.5
    center_dis = np.square(boxes1_center[...,0]-boxes2_center[...,0]) +\
                 np.square(boxes1_center[...,1]-boxes2_center[...,1])

    #cal diou
    dious = ious - center_dis / outer_diagonal_line

    return dious