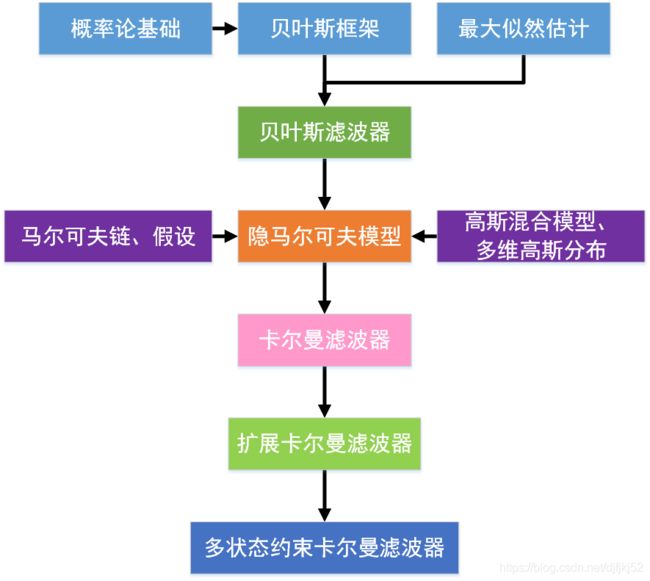
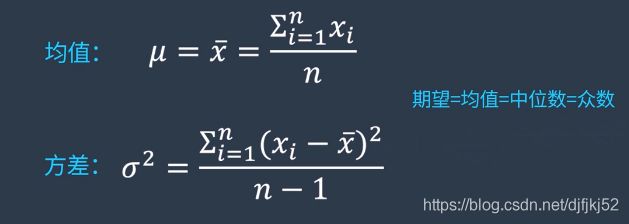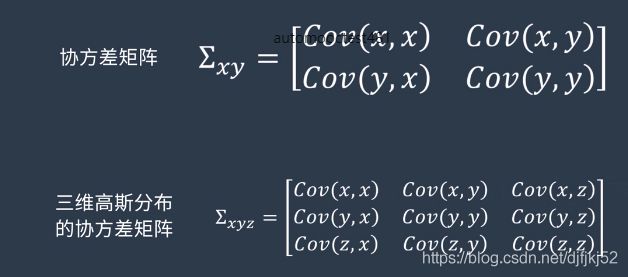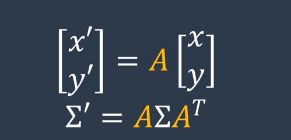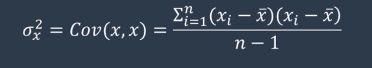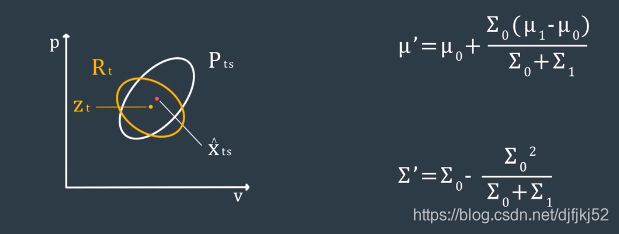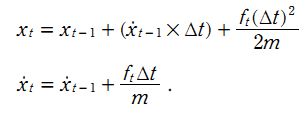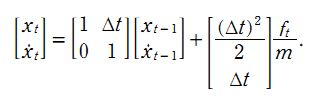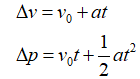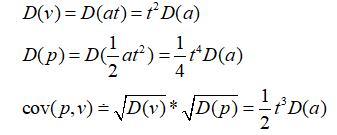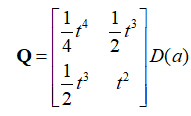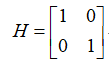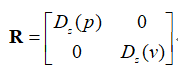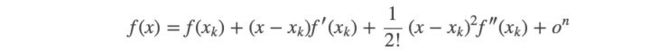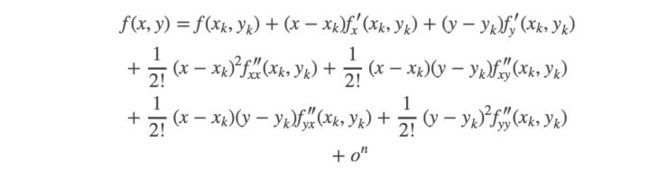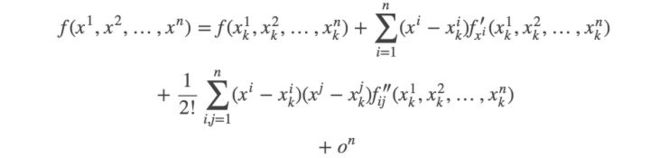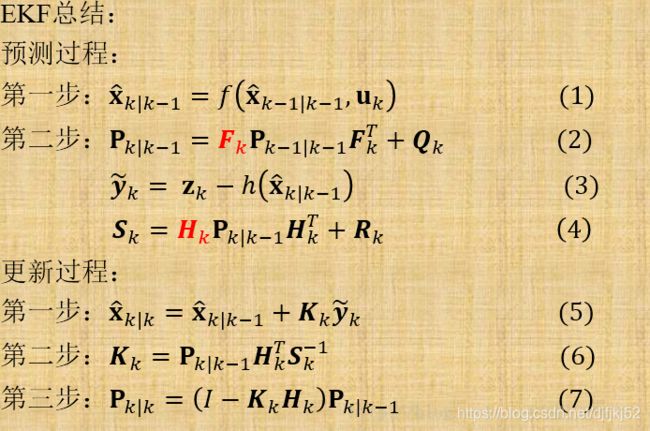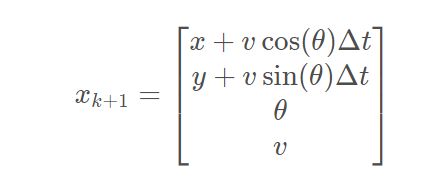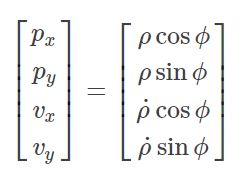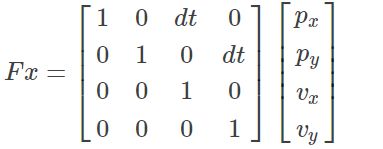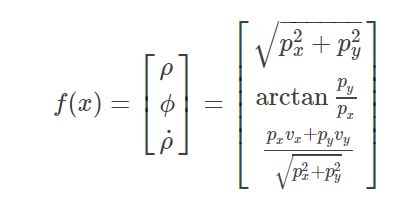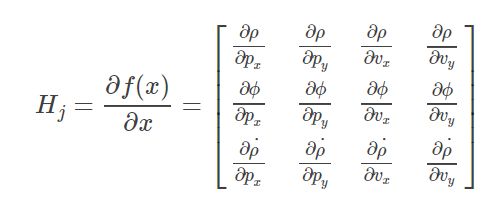3月15日 卡尔曼与多元传感器融合
文章目录
-
- bayes
- 卡尔曼推导(可以跳过)
-
- 1.0定义
- 2.0文献
- 3.0基本动态系统模型
- 3.1两个模型——状态转移和观测:
- 3.2纯粹的时域滤波器
- 3.3卡尔曼滤波器的状态
- 3.4直接点说,只要能写出B,Q,R,H和F矩阵的动态系统,都能用卡尔曼滤波解决动态状态估计问题。
- 3.5 过程一:预测
- 3.6过程二:更新
-
- 总结更新过程:
- 3.6.1 最优卡尔曼增益
- 3.7不变量(Invariant)
-
- 参考reference:
- 传统 KF 分析小车运动(不是多源融合)
-
- 1、运动与观测
- 2、对于状态方程中的系统噪声w和测量噪声v,假设服从如下多元高斯分布,并且w,v是相互独立的。其中Q,R为噪声变量的协方差矩阵。
- 3、初值 P K P_K PK
- 协方差矩阵的计算(可以了解)
- (四)总结
- 附上某bilibili课件图片
- CRTV等汽车运动模型
- 例子
- 多元高斯分布协方差矩阵
- 拓展卡尔曼
-
- 关于泰勒展开的故事:
-
- 泰勒展开,初值对估计的影响
- 推导过程(可以忽略)
- 言归正传:
- EKF的线性化采用一阶泰勒展开
- 实际上python中有专门计算梯度和雅克比矩阵的库numdifftools
- 过程总结
- EKF-近似最优卡尔曼增益
- 状态向量的选取经验(可以略过)
- EKF 例子
- 另一种EKF_error state KF
- 多传感器融合-lidar+Radar
-
- 初始化
- 预测
- 修正
-
- lidar使用了KF
- radar使用了EKF
- 传感器融合实例
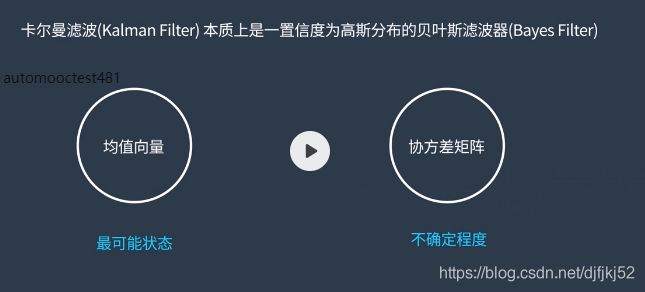
卡尔曼滤波器是在估计线性系统状态的过程中, 以最小均方误差为目的而推导出的几个递推数学等式。
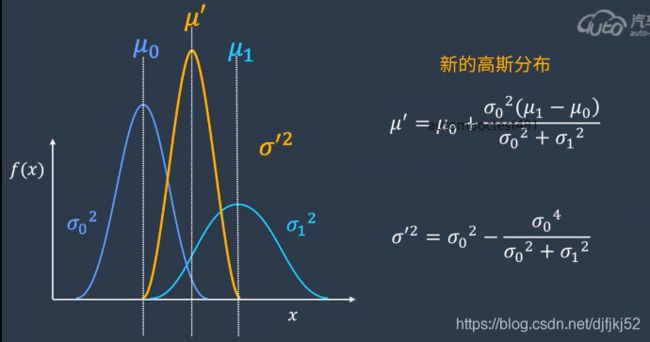
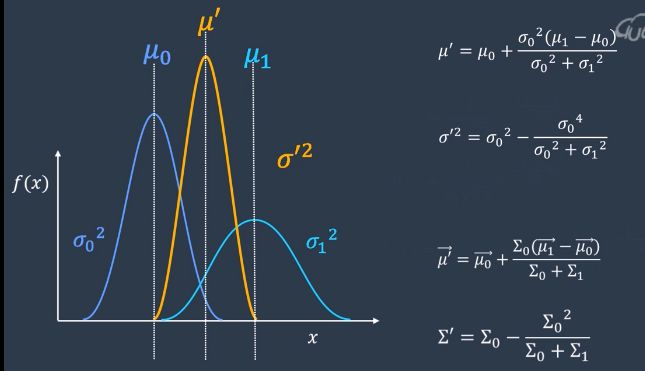
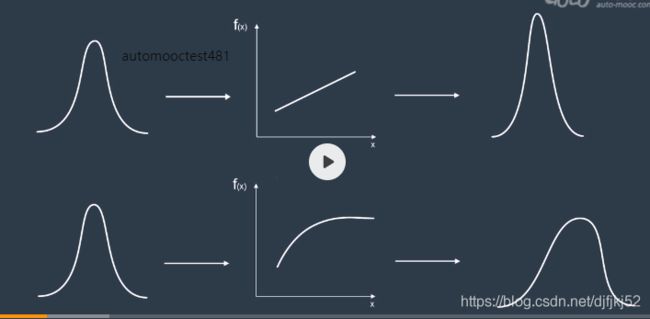
也可以从贝叶斯推断的角度来推导,如下图。
bayes
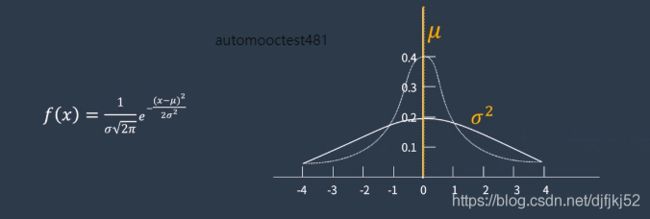
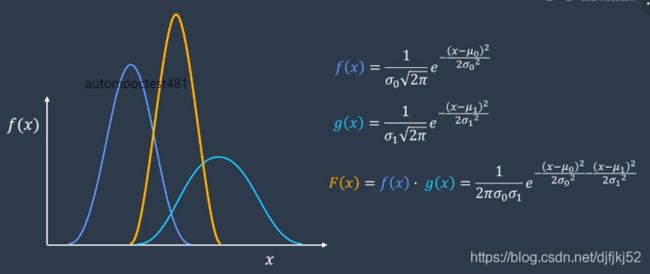
高斯分布
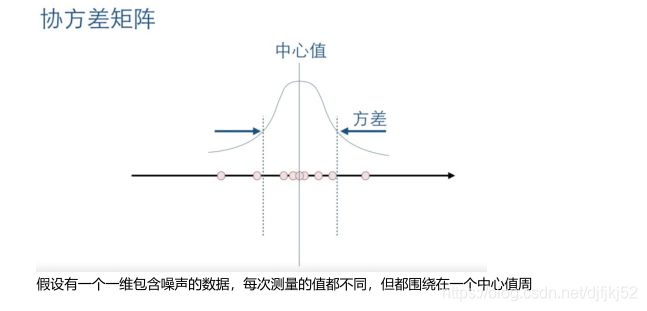
协方差在概率论和统计学中用于衡量两个变量的总体误差,其实方差就是协方差的一种特殊情况,可以理解为两个相同变量的协方差
对于两个相互独立的高斯分布,我们将他们的概率密度相乘
卡尔曼推导(可以跳过)
1.0定义
卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。这个估计可以是对当前目标位置的估计(滤波),也可以是对于将来位置的估计(预测),也可以是对过去位置的估计(插值或平滑)。——维基百科
2.0文献
http://www.cs.unc.edu/~welch/kalman/media/pdf/Kalman1960.pdf
3.0基本动态系统模型
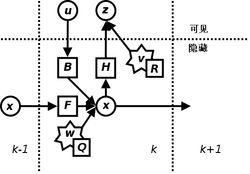
基本动态系统可以用一个马尔可夫链表示,该马尔可夫链建立在一个被高斯噪声(即正态分布的噪声)干扰的线性算子上的[1]。
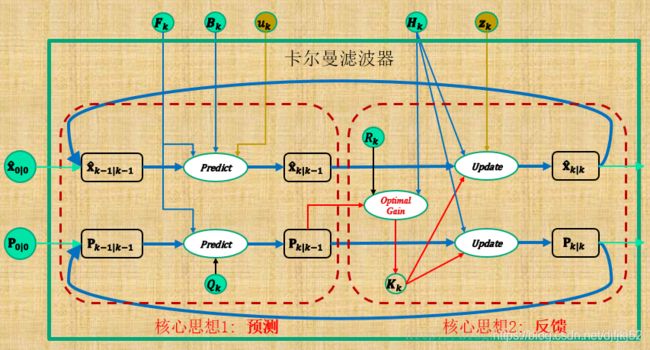
卡尔曼滤波器的模型。圆圈代表向量,方块代表矩阵,星号代表高斯噪声,其协方差矩阵在右下方标出。
从一系列有噪声的观察数据中用卡尔曼滤波器估计出被观察过程的内部状态.对于每一步k,定义矩阵 F k , H k , Q k , R k F_k, H_k, Q_k,R_k Fk,Hk,Qk,Rk,有时也需要定义 B k B_k Bk。
And,
F k F_k Fk是作用在 x k − 1 x_{k−1} xk−1上的状态变换模型(/矩阵/矢量)。
B k B_k Bk是作用在控制器向量 u k u_k uk上的输入-控制模型。
w k w_k wk是过程噪声,并假定其符合均值为零,协方差矩阵为 Q k Q_k Qk的多元正态分布。 W k N ( 0 , Q k ) W_k~N(0,Q_k) Wk N(0,Qk).
H k H_k Hk是观测模型,它把真实状态空间映射成观测空间, v k v_k vk是观测噪声,其均值为零,协方差矩阵为 R k R_k Rk,且服从正态分布。 V k N ( 0 , R k ) V_k~N(0,R_k) Vk N(0,Rk)
3.1两个模型——状态转移和观测:
假设 k k k时刻的真实状态是从 ( k − 1 ) (k − 1) (k−1)时刻的状态演化,[Control Model]
x k = F k x k − 1 + B k u k − 1 + w k − 1 x_k=F_kx_{k-1}+B_ku_{k-1}+w_{k-1} xk=Fkxk−1+Bkuk−1+wk−1
k k k时刻,对真实状态 x k x_k xk的一个测量 z k z_k zk满足下式:[Observation Model]
z k = H k x k + v k z_k=H_kx_k+v_k zk=Hkxk+vk
3.2纯粹的时域滤波器
卡尔曼滤波是一种递归的估计,即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值, 因此不需要记录观测或者估计的历史信息。卡尔曼滤波器与大多数滤波器不同之處,在於它是一种纯粹的时域滤波器,它不需要像低通滤波器等频域滤波器那样,需要在频域设计再转换到时域实现。
3.3卡尔曼滤波器的状态
卡尔曼滤波器的状态由以下两个变量表示:
x ^ k ∣ k \hat{x}_{k|k} x^k∣k:在时刻k的状态的估计;
P k ∣ k P_{k|k} Pk∣k:误差相关矩阵,度量估计值的精确程度。
3.4直接点说,只要能写出B,Q,R,H和F矩阵的动态系统,都能用卡尔曼滤波解决动态状态估计问题。
3.5 过程一:预测
卡尔曼滤波器的操作包括两个阶段:预测与更新。在预测阶段,滤波器使用上一状态的估计,做出对当前状态的估计。在更新阶段,滤波器利用对当前状态的观测值优化在预测阶段获得的预测值,以获得一个更精确的新估计值。
1.(预测状态)
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1 + B k u k \hat{x}_{k|k-1}=F_{k}\hat{x}_{k-1|k-1}+B_ku_{k} x^k∣k−1=Fkx^k−1∣k−1+Bkuk
2.(预测估计协方差矩阵)
P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k P_{k|k-1}=F_kP_{k-1|k-1}F_k^{T}+Q_k Pk∣k−1=FkPk−1∣k−1FkT+Qk
3.6过程二:更新
首先要算出以下三个量:
y ~ k = z k − H k x ^ k ∣ k − 1 \tilde{\textbf{y}}_{k} = \textbf{z}_{k} - \textbf{H}_{k}\hat{\textbf{x}}_{k|k-1} y~k=zk−Hkx^k∣k−1(测量余量,measurement residual)
S k = H k P k ∣ k − 1 H k T + R k \textbf{S}_{k} = \textbf{H}_{k}\textbf{P}_{k|k-1}\textbf{H}_{k}^{T} + \textbf{R}_{k} Sk=HkPk∣k−1HkT+Rk(测量余量协方差)
K k = P k ∣ k − 1 H k T S k − 1 \textbf{K}_{k} = \textbf{P}_{k|k-1}\textbf{H}_{k}^{T}\textbf{S}_{k}^{-1} Kk=Pk∣k−1HkTSk−1(最优卡尔曼增益)
然后用它们来更新滤波器变量 X k , P k X_k ,P_k Xk,Pk:
x ^ k ∣ k = x ^ k ∣ k − 1 + K k y ~ k \hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}_{k|k-1} + \textbf{K}_{k}\tilde{\textbf{y}}_{k} x^k∣k=x^k∣k−1+Kky~k(更新的状态估计)
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 \textbf{P}_{k|k} =(I - \textbf{K}_{k} \textbf{H}_{k}) \textbf{P}_{k|k-1} Pk∣k=(I−KkHk)Pk∣k−1(更新的协方差估计)
使用上述公式计算 P k ∣ k \textbf{P}_{k|k} Pk∣k仅在最优卡尔曼增益的时候有效。使用其他增益的话,公式要复杂一些。
高斯分布经过线性变换后还是高斯分布
高斯分布经过非线性变换后还是非高斯分布
总结更新过程:
x ^ k ∣ k = x ^ k ∣ k − 1 + K k y ~ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) = ( 1 − K k H k ) x ^ k ∣ k − 1 + K k z k \hat{ {x}}_{k|k} = \hat{ {x}}_{k|k-1} + {K}_{k}\tilde{ {y}}_{k}=\hat{ {x}}_{k|k-1} + {K}_{k}({z}_{k} - {H}_{k}\hat{ {x}}_{k|k-1})=(1- {K}_{k}{H}_{k})\hat{ {x}}_{k|k-1}+{K}_{k}{z}_{k} x^k∣k=x^k∣k−1+Kky~k=x^k∣k−1+Kk(zk−Hkx^k∣k−1)=(1−KkHk)x^k∣k−1+Kkzk
x ^ k ∣ k − 1 \hat{ {x}}_{k|k-1} x^k∣k−1是基于k-1时刻的最优估计和模型(先验分布)得到的预测值, z k {z}_{k} zk是k时刻的观测值,也就是说,我们的最优估计实际上是对测量值和预测值的一个加权平均,而 P k ∣ k {P}_{k|k} Pk∣k就是迭代过程中的最优加权系数(实际上是根据方差确定比例)。
3.6.1 最优卡尔曼增益
- https://blog.csdn.net/u013102281/article/details/59109566?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
最优卡尔曼增益, P k ∣ k = ( I − K k H k ) P k ∣ k − 1 \textbf{P}_{k|k} =(I - \textbf{K}_{k} \textbf{H}_{k}) \textbf{P}_{k|k-1} Pk∣k=(I−KkHk)Pk∣k−1(更新的协方差估计)这个公式的计算比较简单,所以实际中总是使用这个公式,但是需注意这公式仅在使用最优卡尔曼增益的时候它才成立。如果算术精度总是很低而导致数值稳定性出现问题,或者特意使用非最优卡尔曼增益,那么就不能使用这个简化;必须使用导出的后验误差协方差公式。
此式可以写作
P k ∣ k = ( I − K k H k ) cov ( x k − x ^ k ∣ k − 1 , I − K k H k ) T + K k cov ( v k ) K k T \textbf{P}_{k|k} =(I - \textbf{K}_k \textbf{H}_{k})\textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1},I - \textbf{K}_k \textbf{H}_{k})^{T} + \textbf{K}_k\textrm{cov}(\textbf{v}_k )\textbf{K}_k^{T} Pk∣k=(I−KkHk)cov(xk−x^k∣k−1,I−KkHk)T+Kkcov(vk)KkT
使用不变量 P k ∣ k − 1 P_{k|k-1} Pk∣k−1以及 R k R_k Rk的定义这一项可以写作 :
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T \textbf{P}_{k|k}=(I - \textbf{K}_k \textbf{H}_{k}) \textbf{P}_{k|k-1}(I - \textbf{K}_k \textbf{H}_{k})^T +\textbf{K}_k \textbf{R}_k \textbf{K}_k^T Pk∣k=(I−KkHk)Pk∣k−1(I−KkHk)T+KkRkKkT 这一公式对于任何卡尔曼增益 K k K_k Kk都成立。
参考:https://blog.csdn.net/DinnerHowe/article/details/79483194 推导 P k ∣ k P_{k|k} Pk∣k的过程。
3.7不变量(Invariant)
如果模型准确,而且 x ^ 0 ∣ 0 \hat{\textbf{x}}_{0|0} x^0∣0与 P 0 ∣ 0 \textbf{P}_{0|0} P0∣0的值准确的反映了最初状态的分布,那么以下不变量就保持不变:所有估计的误差均值为零
E [ x k − x ^ k ∣ k ] = E [ x k − x ^ k ∣ k − 1 ] = 0 \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0 E[xk−x^k∣k]=E[xk−x^k∣k−1]=0
E [ y ~ k ] = 0 \textrm{E}[\tilde{\textbf{y}}_k] = 0 E[y~k]=0
且协方差矩阵准确的反映了估计的协方差:
P k ∣ k = cov ( x k − x ^ k ∣ k ) \textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k}) Pk∣k=cov(xk−x^k∣k)
P k ∣ k − 1 = cov ( x k − x ^ k ∣ k − 1 ) \textbf{P}_{k|k-1} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}) Pk∣k−1=cov(xk−x^k∣k−1)
S k = cov ( y ~ k ) \textbf{S}_{k} = \textrm{cov}(\tilde{\textbf{y}}_k) Sk=cov(y~k)
请注意,其中 E [ a ] \textrm{E}[\textbf{a}] E[a]表示 a {a} a的期望值,
cov ( a ) = E [ a a T ] \textrm{cov}(\textbf{a}) = \textrm{E}[\textbf{a}\textbf{a}^T] cov(a)=E[aaT]。
参考reference:
[1]卡尔曼滤波算法原理以及python实例https://blog.csdn.net/DinnerHowe/article/details/79483194
[2]https://blog.csdn.net/banzhuan133/article/details/103570744
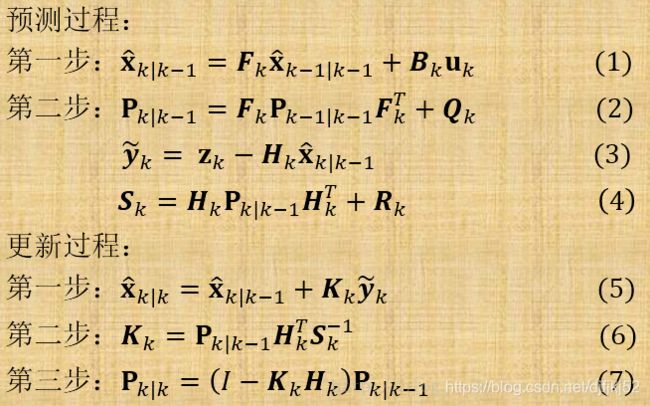
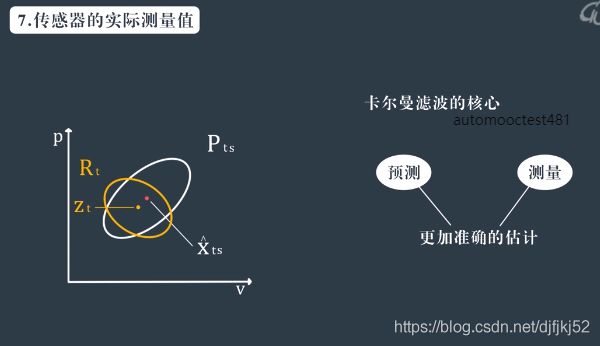
图源:https://blog.csdn.net/u013102281/article/details/59109566?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
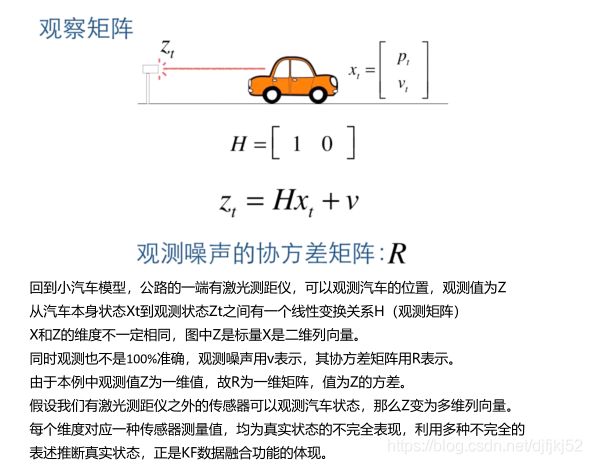
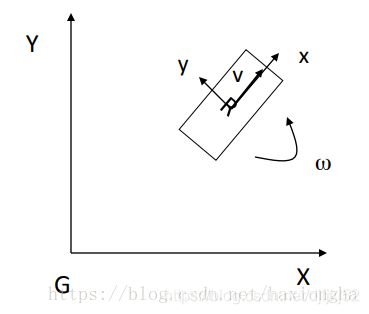
传统 KF 分析小车运动(不是多源融合)
有一个匀加速运动的小车,它受到的合力为 ft , 由匀加速运动的位移和速度公式,能得到由 t-1 到 t 时刻的位移和速度变化公式:
1、运动与观测
该系统系统的状态向量包括位移和速度,分别用 xt 和 xt的导数 表示。控制输入变量为u,也就是加速度,于是有如下形式:
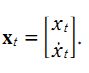
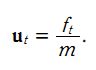
x k = F k x k − 1 + B k u k − 1 + w k − 1 x_k=F_kx_{k-1}+B_ku_{k-1}+w_{k-1} xk=Fkxk−1+Bkuk−1+wk−1
这里对应的的矩阵F大小为 2x2 ,矩阵B大小为 2x1。
用超声波仪器测量小车离我们的距离 :
z k = H k x k + v k z_k=H_kx_k+v_k zk=Hkxk+vk
2、对于状态方程中的系统噪声w和测量噪声v,假设服从如下多元高斯分布,并且w,v是相互独立的。其中Q,R为噪声变量的协方差矩阵。
w k — — N ( 0 , Q k ) w_k——N(0,Q_k) wk——N(0,Qk).
v k — — N ( 0 , R k ) v_k——N(0,R_k) vk——N(0,Rk)
对于小车匀加速运动的的模型,假设系统的噪声向量只存在速度分量上,且速度噪声的方差是一个常量0.01,位移分量上的系统噪声为0。Q中,叠加在速度上系统噪声方差为0.01,位移上的为0,它们间协方差为0,即噪声间没有关联。
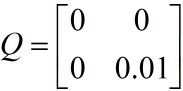
测量值只有位移,它的协方差矩阵大小是1*1,就是测量噪声的方差本身。
R = [ 0.1 ] 1 × 1 R=[0.1]_{1×1} R=[0.1]1×1
3、初值 P K P_K PK
估计值和真实值间误差的协方差矩阵 P k − 1 ∣ k − 1 P_{k-1|k-1} Pk−1∣k−1,协方差矩阵的对角线元素就是方差,求这个协方差矩阵,就是为了利用他的对角线元素的和计算得到均方差.
![]()
如果是匀加速运动模型里,ek便是由位移误差和速度误差,他们组成的协方差矩阵。
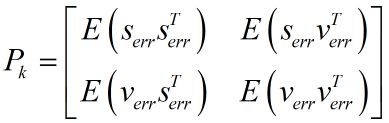
其中,Serr代表位移误差,Verr代表速度误差,对角线上就是各自的方差。
更新 P K P_K PK
P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k P_{k|k-1}=F_kP_{k-1|k-1}F_k^{T}+Q_k Pk∣k−1=FkPk−1∣k−1FkT+Qk
协方差矩阵的计算(可以了解)
- https://blog.csdn.net/u011362822/article/details/95905113
在整个kalmam滤波的操作过程中,有3个协方差矩阵是需要特殊注意的,也是很多人使用时不知如何设置和更新的,分别是状态协方差矩阵P,过程噪声协方差矩阵Q,测量噪声协方差矩阵R。
(一)状态协方差矩阵P
状态协方差矩阵P就是状态之间的协方差组成的矩阵,对角线元素是各个状态的方差,其余元素是相应元素的协方差,由此也能看出P是一个多维方阵,维度和状态数一致,且P是对称方阵。
比如状态X包含位置p和速度v两个量,则对应的协方差矩阵如下式所示:
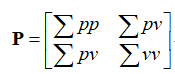
由于相同变量之间的协方差就是其方差,因此对角线上元素分别是p和v的方差,其余两个元素分别是两元素间的协方差,由于协方差部分次序,协方差矩阵式对称的。
在使用时协方差矩阵P是一个迭代更新的量,每一轮预测和更新后,P都会更新一个新的值,因此初始化时可以根据估计协定,不用太苛求初始化的精准度,因为随着几轮迭代会越来越趋紧真实值。
(二)过程误差协方差矩阵Q
该矩阵的每一个元素分别是状态X的元素误差之间的协方差,以上文中的状态X为例,其包含位置p和速度v两个元素,其误差状态为:
![]()
其Q矩阵可用下式表示:
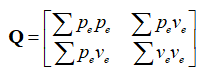
该矩阵是由不确定的噪声引起的,确定Q的各元素大小是不容易的,使用时都是具体问题具体分析。
比方说针对上文中的小车的状态,误差来源是移动中的打滑等,最底层的是由于力的变化导致的加速度的变化,因此我们找到了加速度方差,就可以推导出Q矩阵,假设加速度方差是D(a)。
(三)测量噪声协方差矩阵R
测量噪声协方差的来源是传感器误差,即传感器的不准确性,在使用时一般传感器都会给出精度指标,该指标就可以直接转化到矩阵R中。
还以上文小车为例,假设测量矩阵为下式所示:
表示状态X中的位置p和速度v均可以测量,观测误差协方差矩阵R用下式表示:

此时对角线上就是各测量量的测量方差,从传感器说明书上均可以读到,另外针对状态之间的协方差吐过确定不了就可以设为0,即可以如下设置:
(四)总结
P矩阵可以根据状态方差估计,不用太最求准确度,因为P矩阵会随着迭代次数的增加而收敛到准确值;
Q矩阵是状态转移预测过程由于外部干扰产生,移动机器人中可以运动加速度的方差来推导,此时只要估计一个加速度的方差即可;
R矩阵是传感器测量的不准确度,每个每个传感器都会给出测量对向的准确度,直接转换就能用。
附上某bilibili课件图片
CRTV等汽车运动模型
这里再扩展说一下模型的作用,模型决定了预测的计算公式。只要是模型就一定有误差,但ν~N(0,Q)可能不成立,那么就要找到平均值完成运算,并在末端加上ν~N(0,Q)。总之要明确把误差零均值化!!!(算标准差也是先零均值化的)然后基于ν~N(0,Q)完成P’预测。
- 对原始数据进行中心化(Zero-centered(零均值化)或者Mean-subtraction(subtraction表示减去))处理,中心化(零均值化)后的数据均值为零
- 对原始数据进行标准化(Standardization或Normalization(归一化))处理
- https://blog.csdn.net/GoodShot/article/details/80373372
- 图源:https://blog.csdn.net/qq_42258099/article/details/99601467
先说明Q,再说明一下 F P F T FPF^T FPFT。
前面说明了P是用来说明X的数值精确度以及参量之间的相关性。 P ‘ ( P ^ ) P‘(\hat{P}) P‘(P^)就是要更新P并考虑上预测误差。
已知ν~N(0,Q),v即为误差,那么根据协方差公式,求出Q,描述 X ^ \hat{X} X^的协方差矩阵,其中对角代表各参数值的精确度,越小越精确;对角外其他数值代表两个参数间的相关性,0代表不相关,数值越大相关性越强。
F P F T FPF^T FPFT,通过对比说明:
假设p~N(u,σ), X ^ \hat{X} X^就相当于这里的u均值,σ相当于 P ^ \hat{P} P^方差(协方差),表示p是关于X的方差为σ的分布
我们可以对于p进行拉伸、缩放、平移等操作,那么u,σ都会随之而变换,其中σ不会因平移而变化,但对于拉伸、缩放就会发生变化,而 F P F T FPF^T FPFT就是这样的作用,F是状态变化.
例子
% 初始化参数
delta_t=0.1; %采样时间
t=0:delta_t:5;
N = length(t); % 序列的长度
sz = [2,N]; % 信号需开辟的内存空间大小 2行*N列 2:为状态向量的维数n
g=10; %加速度值
x=1/2*g*t.^2; %实际真实位置
z = x + sqrt(10).*randn(1,N); % 测量时加入测量白噪声
Q =[0 0;0 9e-1]; %假设建立的模型 噪声方差叠加在速度上 大小为n*n方阵 n=状态向量的维数
R = 10; % 位置测量方差估计,可以改变它来看不同效果 m*m m=z(i)的维数
A=[1 delta_t;0 1]; % n*n
B=[1/2*delta_t^2;delta_t];
H=[1,0]; % m*n
n=size(Q); %n为一个1*2的向量 Q为方阵
m=size(R);
% 分配空间
xhat=zeros(sz); % x的后验估计
P=zeros(n); % 后验方差估计 n*n
xhatminus=zeros(sz); % x的先验估计
Pminus=zeros(n); % n*n
K=zeros(n(1),m(1)); % Kalman增益 n*m
I=eye(n);
% 估计的初始值都为默认的0,即P=[0 0;0 0],xhat=0
for k = 9:N %假设车子已经运动9个delta_T了,我们才开始估计
% 时间更新过程
xhatminus(:,k) = A*xhat(:,k-1)+B*g;
Pminus= A*P*A'+Q;
% 测量更新过程
K = Pminus*H'*inv( H*Pminus*H'+R );
xhat(:,k) = xhatminus(:,k)+K*(z(k)-H*xhatminus(:,k));
P = (I-K*H)*Pminus;
end
多元高斯分布协方差矩阵
两个随机变量的协方差表现的是两个变量之间的相关关系;自己跟自己的协方差就是方差。协方差可以求解相关系数。
独立关系:两个随机变量不存在任何关系(包括线性关系),独立必不相关
相关关系:存在线性关系。不相干未必独立
二维随机变量,4个二阶中心矩组成了协方差矩阵
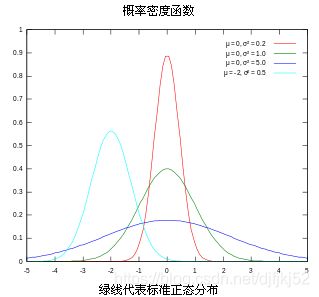
多元高斯分布,高斯公式中的方差也变成了协方差,对应上面三张图的协方差矩阵分别如下:
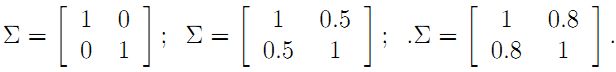
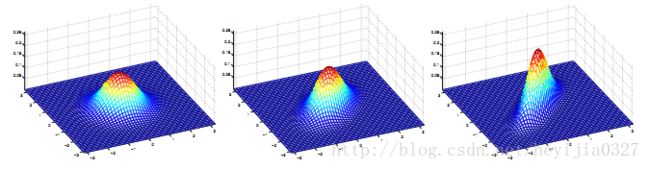
拓展卡尔曼
关于泰勒展开的故事:
- https://www.zhihu.com/question/25627482
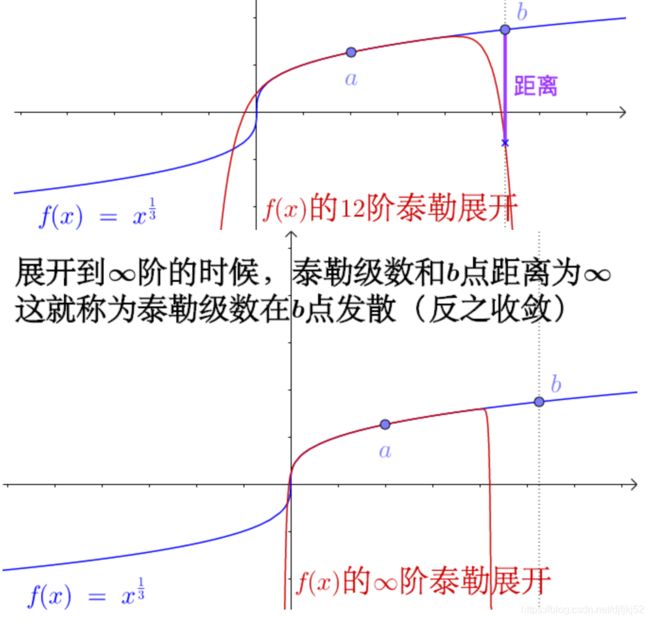
泰勒展开式就是把一个三角函数或者指数函数或者其他比较难缠的函数用多项式替换掉。
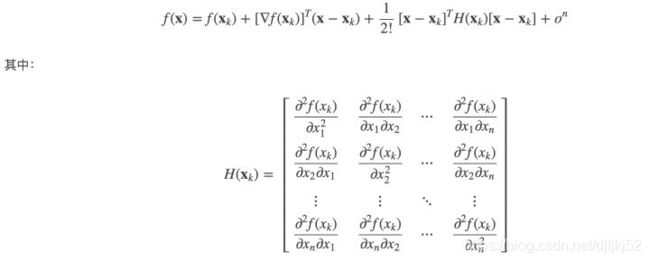
有一个原函数 f ( x ) f(x) f(x),我再造一个图像与原函数图像相似的多项式函数 g ( x ) g(x) g(x) ,为了保证相似,我只需要保证这俩函数在某一点 x 0 x_0 x0的初始值相等,1阶导数相等,2阶导数相等,……n阶导数相等。
麦克劳林级数 是 x 0 = 0 x_0=0 x0=0 的泰勒级数。我们上面的例子都是 麦克劳林级数。
泰勒展开,初值对估计的影响
推导过程(可以忽略)
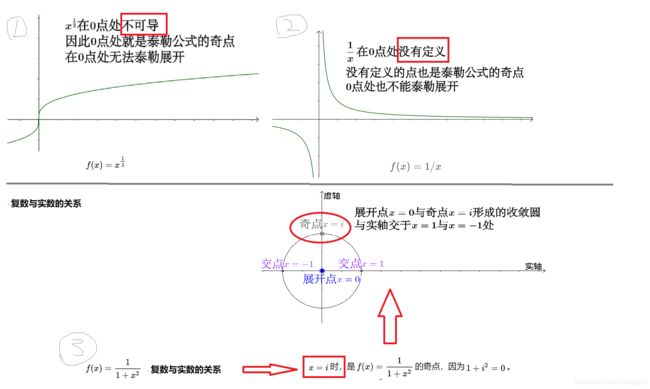
2、奇点
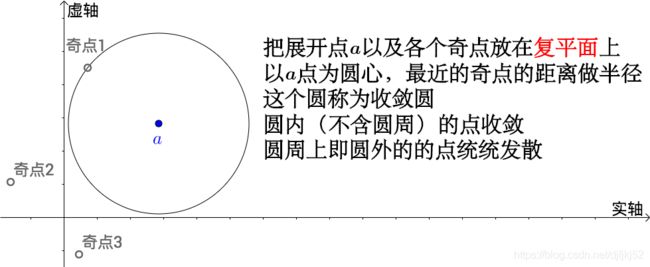
3、 奇点与收敛圆
通过奇点来判断泰勒级数的收敛,非常漂亮的数学结论,由柯西证明的泰勒级数的收敛半径:
言归正传:
卡尔曼滤波的优点有很多,但同样也有一个问题,只适用于线性模型,对上面几种模型来说,出现非线性项(比如cos, sin)时,就无法利用上面的结论了。处理非线性问题最常见的一种思路就是线性化,而对线性化我们有一种强大的工具-泰勒展开。
EKF的线性化采用一阶泰勒展开
KF与EKF的区别如下:
预测: x ^ = F x + u \hat{x}=Fx+u x^=Fx+u用 x ^ = f ( x , u ) \hat{x}=f(x,u) x^=f(x,u)代替;其余状态转移矩阵 F F F用雅克比矩阵 F j F_j Fj代替。
修正:将状态映射到测量的 H x ^ H\hat{x} Hx^用 h ( x ^ ) h(\hat{x}) h(x^)代替;其余观测矩阵 H H H用雅克比矩阵 H j H_j Hj。
假设状态有n维,则求法如下:
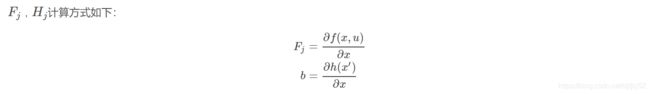
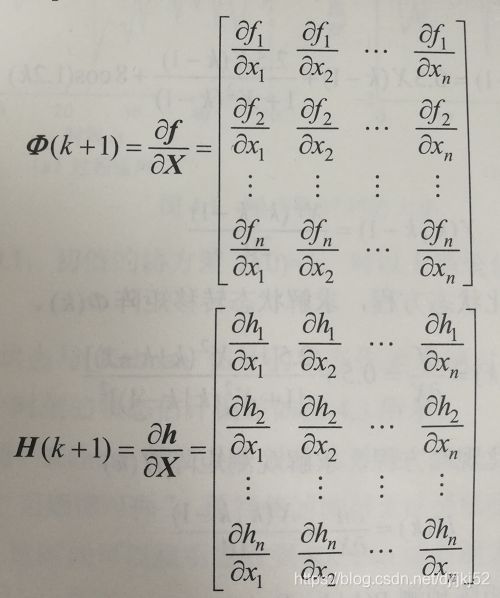
其中,
非线性函数 f ( x , u ) , h ( x ^ ) f(x,u),h(\hat{x}) f(x,u),h(x^)用非线性得到了更精准的状态预测值、映射后的测量值;
线性变换 F j , H j F_j,H_j Fj,Hj线性变换使得变换后的 x , z x,z x,z仍满足高斯分布的假设。
实际上python中有专门计算梯度和雅克比矩阵的库numdifftools
#! /usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
import math
import numdifftools as nd
dt = 0.5
def f(x):
return np.array([x[0]+math.cos(x[2])*x[3]*dt,
x[1]+math.sin(x[2])*x[3]*dt,
x[2], x[3]])
Jfun = nd.Jacobian(f)
print(Jfun([1,2,math.pi,3]))
过程总结
可以看出,EKF依然是在KF的框架内进行的改进,所以思路与KF是完全一致的。只是这里写 H j H_j Hj描述与这里写 F j F_j Fj描述的计算方法不同。
EKF-近似最优卡尔曼增益
此处为什么是近似最优卡尔曼增益而不是最优卡尔曼增益。这是因为计算 H j H_j Hj和 F j F_j Fj的时候理论上应该计算函数 H j H_j Hj和 F j F_j Fj的雅可比矩阵。但是实际操作起来非常困难,特别是对于一些复杂的非线性系统。因此往往采用泰勒展开去一阶线性的部分。由于近似,得到的卡尔曼在增益也就不是最优卡尔曼增益,而是近似最优卡尔曼增益。这就直接导致了EKF在高度非线性系统下性能锐减的必然结果。而且系统初始状态估计错误或者说建模不正确,EKF也会迅速发散。
状态向量的选取经验(可以略过)
EKF 例子
对应的雅克比矩阵为:
由于是匀速过程,那么这里 u k = 0 u_k=0 uk=0对于过程噪声,实际上就是车子加速度 a a a,因此可以认为协方差矩阵Q满足 Q = E ( v v T ) Q=E(vv^T) Q=E(vvT) ,其中
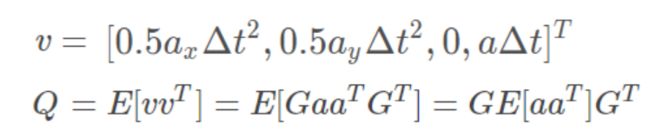
对于观测矩阵,一般汽车就只能读到实时速度,因此 H = [ 0 , 0 , 0 , 1 ] H=[0,0,0,1] H=[0,0,0,1] ,对应的协方差矩阵为 R = δ v 2 R=δ^2_v R=δv2 ,R为观测噪声
在测量值只有速度,存在过程噪声和测量噪声的情况下,利用卡尔曼滤波去得到一个最优的状态估计
#! /usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import math
## x,p,dt,theta,v参数
x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T #状态变量[x, y, theta, v]
P = np.diag([1.0, 1.0, 1.0, 1.0]) #误差矩阵
dt = 0.1 # 时间间隔
theta = math.pi/6
v = 10 # 速度,匀速运动
F = np.matrix([[1.0, 0.0, -v * math.sin(theta) * dt, math.cos(theta) * dt],
[0.0, 1.0, v * math.cos(theta) * dt, math.sin(theta) * dt],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]]) #状态转移矩阵
H = np.matrix([[0.0, 0.0, 0.0, 1.0]]) #观测矩阵
R = 0.25 # 观测方差
deltav = 0.5
v = np.matrix([[0.5*dt**2],
[0.5*dt**2],
[0],
[dt]])
Q = v*v.T*deltav**2 #过程协方差矩阵
I = np.eye(4)
m = 200 # 测量数据数
## 数据存储变量
xt = []
yt = []
thetat= []
vt= [] #v估计值
Zv = [] #v观测值
## 保存过程变量
def saveStates(x, Z):
xt.append(float(x[0]))
yt.append(float(x[1]))
thetat.append(float(x[2]))
vt.append(float(x[3]))
Zv.append(float(Z[0]))
## 滤波
def KFfilter():
global x, P, S, K, Z, y
for n in range(m):
## 预测过程
x = F*x
P = F*P*F.T + Q
S = H*P*H.T + R
K = (P*H.T) * np.linalg.pinv(S)
# 更新过程
Z = v + np.random.randn(1) # 测量值
y = Z - (H*x)
x = x + (K*y)
P = (I - (K*H))*P
saveStates(x, Z)
def plot_x():
fig = plt.figure(figsize=(16,9))
plt.plot(range(m),vt, label='$estimateV$')
plt.plot(range(m),Zv, label='$measurementV$')
plt.axhline(v, color = 'red', label='$trueV$')
plt.xlabel('Filter Step')
plt.title('KF Filter')
plt.legend(loc='best')
plt.ylim([5, 15])
plt.ylabel('Velocity')
plt.show()
if __name__ =='__main__':
KFfilter()
plot_x()
另一种EKF_error state KF
error state KF 非线性卡尔曼是对状态误差的转移。

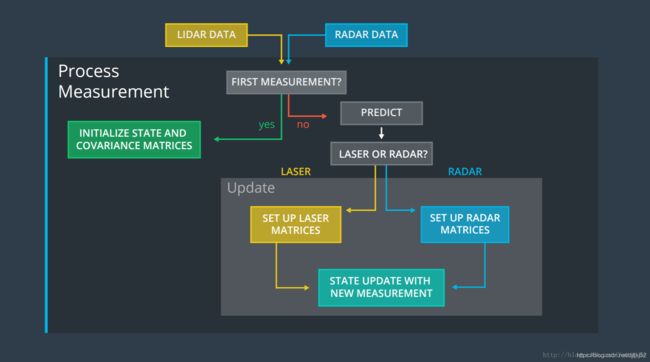
多传感器融合-lidar+Radar
- 链接:https://blog.csdn.net/Young_Gy/article/details/78468153
本文将以汽车跟踪为例,目标是知道汽车时刻的状态 x = ( p x , p y , v x , v y ) x=(p_x,p_y,v_x,v_y) x=(px,py,vx,vy)。已知的传感器有lidar、radar。
lidar:笛卡尔坐标系。可检测到位置,没有速度信息。其测量值 z = ( p x , p y ) z=(p_x,p_y) z=(px,py)。
radar:极坐标系。可检测到距离,角度,速度信息,但是精度较低。其测量值 z = ( ρ , ϕ , ρ ˙ ) z=(ρ,ϕ,ρ˙) z=(ρ,ϕ,ρ˙),图示如下。

初始化
初始化,指在收到第一个测量值后,对状态 x x x进行初始化。初始化如下,同时加上对时间的更新。
对于radar来说,
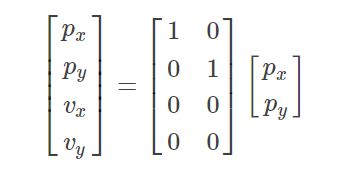
对于lidar来说,
预测
预测主要涉及的公式是:
x ^ = F x \hat{x}=Fx x^=Fx
P k = F P k − 1 F T + Q {P_k}=FP_{k-1}F^T+Q Pk=FPk−1FT+Q
需要求解的有三个变量:F、P、Q。
P表明了系统状态的不确定性程度,用x的协方差表示,这里自己指定为
Q表明了 x ^ = F x \hat{x}=Fx x^=Fx未能刻画的其他外界干扰。本例子使用线性模型,因此加速度变成了干扰项。 x ^ = F x \hat{x}=Fx x^=Fx中未衡量的额外项目v为:
修正
lidar使用了KF
修正当下这里牵涉到的公式主要是:
y ~ = z − H x ^ \tilde{y}=z−H\hat{x} y~=z−Hx^
S = H P k − 1 H T + R S=HP_{k-1}H^T+R S=HPk−1HT+R
K = P k − 1 H T S − 1 K=P_{k-1}H^TS^{−1} K=Pk−1HTS−1
x ^ = x ^ + K y ~ \hat{x}=\hat{x}+K\tilde{y} x^=x^+Ky~
P k = ( I − K H ) P k − 1 P_{k}=(I−KH)P_{k-1} Pk=(I−KH)Pk−1
需要求解的有两个变量:H、R。
R表示了测量值的不确定度,一般由传感器的厂家提供,这里lidar参考如下:
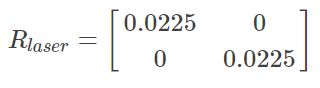
radar使用了EKF
修正当下这里牵涉到的公式主要是:
y ~ = z − f ( x ^ ) \tilde{y}=z−f(\hat{x}) y~=z−f(x^)
S = H j P H j T + R S=H_jPH^T_j+R S=HjPHjT+R
K = P H j T S − 1 K=PH^T_jS^{−1} K=PHjTS−1
x ^ = x ^ + K y ~ \hat{x}=\hat{x}+K\tilde{y} x^=x^+Ky~
P k = ( I − K H j ) P k − 1 P_k=(I−KH_j)P_{k-1} Pk=(I−KHj)Pk−1
区别与上面lidar的主要有:
- 状态空间到测量空间的非线性映射f(x)
- 非线性映射线性化后的Jacob矩阵
- radar的 R r a d a r R_radar Rradar
R 表示了测量值的不确定度,一般由传感器的厂家提供,这里radar参考如下:

传感器融合实例
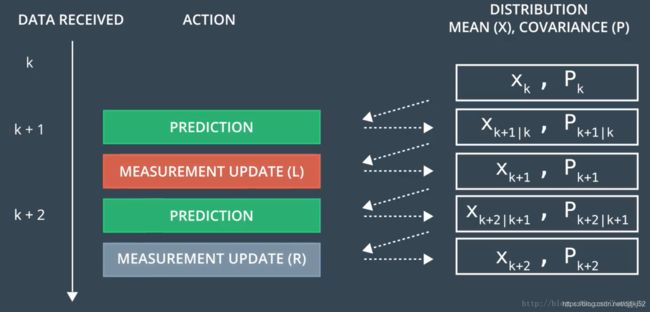
多传感器融合的示例如下,需要注意的有:
- lidar和radar的预测部分是完全相同的
- lidar和radar的参数更新部分是不同的,不同的原因是不同传感器收到的测量值是不同的
- 当收到lidar或radar的测量值,依次执行预测、更新步骤
- 当同时收到lidar和radar的测量值,依次执行预测、更新1、更新2步骤