欢迎关注博主主页,学习python视频资源,还有大量免费python经典文章
![]()
sklearn实战-乳腺癌细胞数据挖掘(博主亲自录制视频教程)
https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share
![]()
最新版本代码
# -*- coding: utf-8 -*-
'''
Author:Toby
QQ:231469242,all right reversed,no commercial use
'''
import scipy
from scipy.stats import f
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# additional packages
from statsmodels.stats.diagnostic import lillifors
group1=[2,3,7,2,6]
group2=[10,8,7,5,10]
group3=[10,13,14,13,15]
list_groups=[group1,group2,group3]
list_total=group1+group2+group3
#正态分布测试
def check_normality(testData):
#20<样本数<50用normal test算法检验正态分布性
if 20=len(testData) >=50:
p_value= lillifors(testData)[1]
if p_value<0.05:
print "use lillifors:"
print "data are not normal distributed"
return False
else:
print "use lillifors:"
print "data are normal distributed"
return True
if len(testData) >300:
p_value= stats.kstest(testData,'norm')[1]
if p_value<0.05:
print "use kstest:"
print "data are not normal distributed"
return False
else:
print "use kstest:"
print "data are normal distributed"
return True
#对所有样本组进行正态性检验
def NormalTest(list_groups):
for group in list_groups:
#正态性检验
status=check_normality(group1)
if status==False :
return False
#对所有样本组进行正态性检验
NormalTest(list_groups)
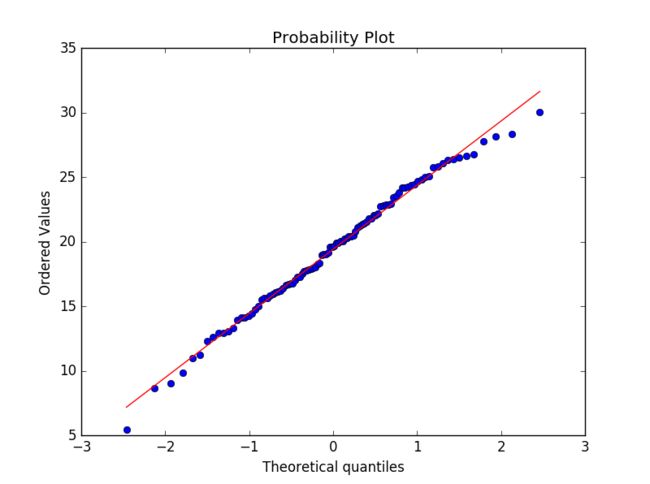
pp-plot和qq-plot结论都很类似。如果数据服从正太分布,生成的点会很好依附在y=x直线上
In all three cases the results are similar: if the two distributions being compared
are similar, the points will approximately lie on the line y D x. If the distributions
are linearly related, the points will approximately lie on a line, but not necessarily
on the line y D x (Fig. 7.1).
In Python, a probability plot can be generated with the command
stats.probplot(data, plot=plt)
https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.probplot.html
sample distribution
In statistics different tools are available for the visual assessments of distributions.
A number of graphical methods exist for comparing two probability distributions by plotting their quantiles, or closely related parameters, against each other:
# -*- coding: utf-8 -*-
import numpy as np
import pylab
import scipy.stats as stats
measurements = np.random.normal(loc = 20, scale = 5, size=100)
stats.probplot(measurements, dist="norm", plot=pylab)
pylab.show()
check for normality of a
http://baike.baidu.com/link?url=o9Z7vr6VdvGAtTRO3RYxQbVu56U_XDaSdibPeVcidMJQ7B6LcAUBHcIro4tLf5BSI5Pu-59W4SPNZ-zRFJ8_FgL3dxJLaUdY0JiB2xUmqie
QQPlot图是用于直观验证一组数据是否来自某个分布,或者验证某两组数据是否来自同一(族)分布。在教学和软件中常用的是检验数据是否来自于正态分布。
# -*- coding: utf-8 -*-
import numpy as np
import statsmodels.api as sm
import pylab
test = np.random.normal(0,1, 1000)
sm.qqplot(test, line='45')
pylab.show()
QQ图显示1000个点很好落在y=x直线附近,所以这些数据有很好正态性。
# -*- coding: utf-8 -*-
from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
nsample = 100
np.random.seed(7654321)
ax1 = plt.subplot(221)
#A t distribution with small degrees of freedom:
#生成自由度3,样本量100的t分布数据,自由度太小,正态分布性较差
x = stats.t.rvs(3, size=nsample)
res = stats.probplot(x, plot=plt)
#A t distribution with larger degrees of freedom:
#自由度大,数据接近正态分布
ax2 = plt.subplot(222)
x2 = stats.t.rvs(25, size=nsample)
res1 = stats.probplot(x2, plot=plt)
#A mixture of two normal distributions with broadcasting:
ax3 = plt.subplot(223)
x3 = stats.norm.rvs(loc=[0,5], scale=[1,1.5],
size=(nsample/2.,2)).ravel()
res = stats.probplot(x3, plot=plt)
#A standard normal distribution:标准正太分布,pp-plot正态性较好
ax4 = plt.subplot(224)
x4 = stats.norm.rvs(loc=0, scale=1, size=nsample)
res = stats.probplot(x4, plot=plt)
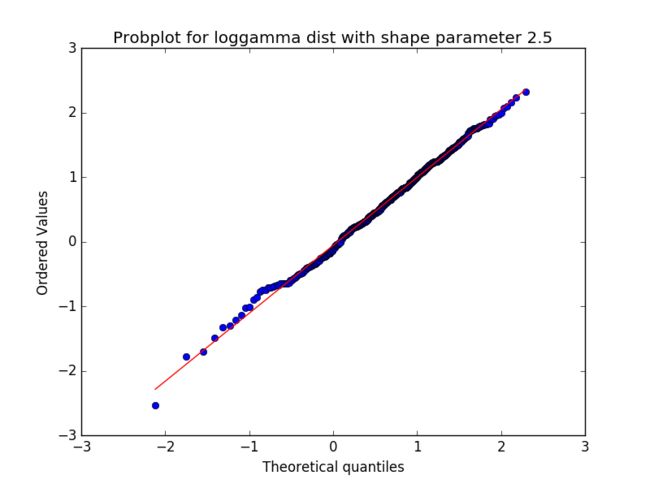
#Produce a new figure with a loggamma distribution, using the dist and sparams keywords:
fig = plt.figure()
ax = fig.add_subplot(111)
x = stats.loggamma.rvs(c=2.5, size=500)
stats.probplot(x, dist=stats.loggamma, sparams=(2.5,), plot=ax)
ax.set_title("Probplot for loggamma dist with shape parameter 2.5")
plt.show()
may be available, while other times one may have many data, but some extremely
outlying values. To cope with the different situations different tests for normality
have been developed. These tests to evaluate normality (or similarity to some
specific distribution) can be broadly divided into two categories:
1. Tests based on comparison (“best fit”) with a given distribution, often specified
in terms of its CDF. Examples are the Kolmogorov–Smirnov test, the Lilliefors
test, the Anderson–Darling test, the Cramer–von Mises criterion, as well as the
Shapiro–Wilk and Shapiro–Francia tests.
2. Tests based on descriptive statistics of the sample. Examples are the skewness
test, the kurtosis test, the D’Agostino–Pearson omnibus test, or the Jarque–Bera
test.
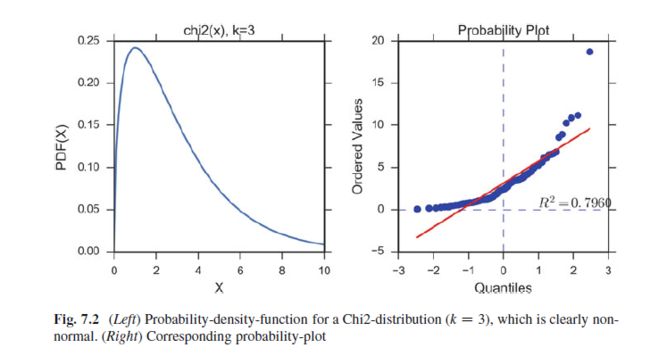
For example, the Lilliefors test, which is based on the Kolmogorov–Smirnov
test, quantifies a distance between the empirical distribution function of the sample
and the cumulative distribution function of the reference distribution (Fig. 7.3),
or between the empirical distribution functions of two samples. (The original
Kolmogorov–Smirnov test should not be used if the number of samples is ca. 300.)
The Shapiro–Wilk W test, which depends on the covariance matrix between the
order statistics of the observations, can also be used with 50 samples, and has been
recommended by Altman (1999) and by Ghasemi and Zahediasl (2012).
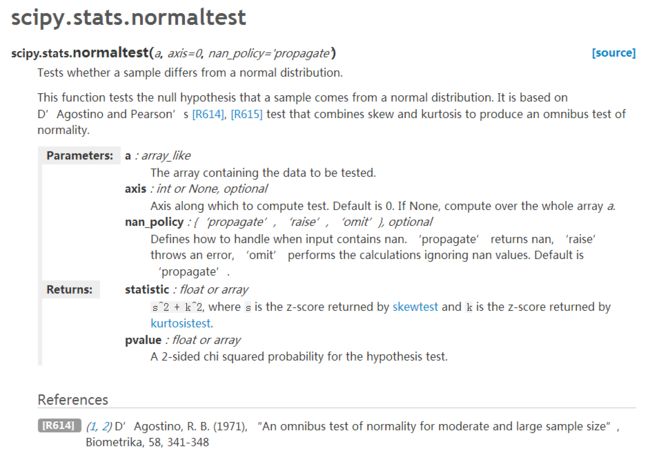
The Python command stats.normaltest(x) uses the D’Agostino–Pearson
omnibus test. This test combines a skewness and kurtosis test to produce a single,
global “omnibus” statistic.
# -*- coding: utf-8 -*-
#bug report [email protected]
'''
Graphical and quantitative check, if a given distribution is normal.
- For small sample-numbers (<50), you should use the Shapiro-Wilk test or the "normaltest"
- for intermediate sample numbers, the Lilliefors-test is good since the original Kolmogorov-Smirnov-test is unreliable when mean and std of the distribution
are not known.
- the Kolmogorov-Smirnov(Kolmogorov-Smirnov) test should only be used for large sample numbers (>300)
'''
# Copyright(c) 2015, Thomas Haslwanter. All rights reserved, under the CC BY-SA 4.0 International License
# Import standard packages
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas as pd
# additional packages
from statsmodels.stats.diagnostic import lillifors
def check_normality():
'''Check if the distribution is normal.'''
# Set the parameters
numData = 1000
myMean = 0
mySD = 3
# To get reproducable values, I provide a seed value
np.random.seed(1234)
# Generate and show random data
data = stats.norm.rvs(myMean, mySD, size=numData)
fewData = data[:100]
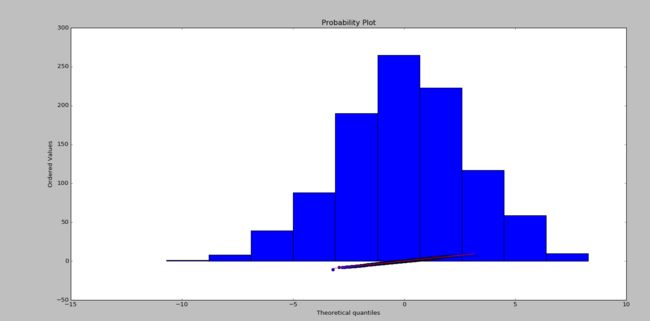
plt.hist(data)
plt.show()
# --- >>> START stats <<< ---
# Graphical test: if the data lie on a line, they are pretty much
# normally distributed
_ = stats.probplot(data, plot=plt)
plt.show()
pVals = pd.Series()
pFewVals = pd.Series()
# The scipy normaltest is based on D-Agostino and Pearsons test that
# combines skew and kurtosis to produce an omnibus test of normality.
_, pVals['Omnibus'] = stats.normaltest(data)
_, pFewVals['Omnibus'] = stats.normaltest(fewData)
# Shapiro-Wilk test
_, pVals['Shapiro-Wilk'] = stats.shapiro(data)
_, pFewVals['Shapiro-Wilk'] = stats.shapiro(fewData)
# Or you can check for normality with Lilliefors-test
_, pVals['Lilliefors'] = lillifors(data)
_, pFewVals['Lilliefors'] = lillifors(fewData)
# Alternatively with original Kolmogorov-Smirnov test
_, pVals['Kolmogorov-Smirnov'] = stats.kstest((data-np.mean(data))/np.std(data,ddof=1), 'norm')
_, pFewVals['Kolmogorov-Smirnov'] = stats.kstest((fewData-np.mean(fewData))/np.std(fewData,ddof=1), 'norm')
print('p-values for all {0} data points: ----------------'.format(len(data)))
print(pVals)
print('p-values for the first 100 data points: ----------------')
print(pFewVals)
if pVals['Omnibus'] > 0.05:
print('Data are normally distributed')
# --- >>> STOP stats <<< ---
return pVals['Kolmogorov-Smirnov']
if __name__ == '__main__':
p = check_normality()
print(p)
normaltest
If my understanding is correct, it indicates how likely the input data is in normal distribution. I had expected that all the pvalues generated by the above code very close to 1.
Your understanding is incorrect, I'm afraid. The p-value is the probability to get a result that is at least as extreme as the observation under the null hypothesis (i.e. under the assumption that the data is actually normal distributed). It does not need to be close to 1. Usually, p-values greater than 0.05 are considered not significant, which means that normality has not been disproved by the test.
As pointed out by Victor Chubukov, you can get low p-values simply by chance, even if the data is really normally distributed.
Statistical hypothesis testing is rather complex and can appear somewhat counter intuitive. If you need to know more details, Cross Validated is the place to get more detailed answers.
# -*- coding: utf-8 -*-
'''
样本量必须大于等于20
UserWarning: kurtosistest only valid for n>=20
'''
import numpy
from numpy import random
from scipy import stats
d = numpy.random.normal(size=1000)
n = stats.normaltest(d)
print (n)
# -*- coding: utf-8 -*-
import numpy,scipy
from numpy import random
from scipy import stats
for i in range(0, 10):
d = numpy.random.normal(size=50000)
n = scipy.stats.normaltest(d)
print (n)
H0:样本服从正太分布
- For small sample-numbers (<50), you should use the Shapiro-Wilk test or the "normaltest"
# -*- coding: utf-8 -*-
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
x = stats.norm.rvs(loc=5, scale=3, size=49)
stats.shapiro(x)
'''
p值大于0.05,H0成立,数据呈现正态分布
Out[9]: (0.9735164046287537, 0.3322194814682007)
'''
plt.hist(x)
Lilliefors-test
适用于中等样本数据
- for intermediate sample numbers, the Lilliefors-test is good since the original Kolmogorov-Smirnov-test is unreliable when mean and std of the distribution are not known.
In statistics, the Lilliefors test, named after Hubert Lilliefors, professor of statistics at George Washington University, is a normality test based on the Kolmogorov–Smirnov test. It is used to test the null hypothesis that data come from a normally distributed population, when the null hypothesis does not specify which normal distribution; i.e., it does not specify the expected value and variance of the distribution.
statsmodels.stats.diagnostic.lilliefors
-
http://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.lilliefors.html
-
lilliefors test for normality,
Kolmogorov Smirnov test with estimated mean and variance
Parameters: x : array_like, 1d
data series, sample
pvalmethod : ‘approx’, ‘table’
‘approx’ uses the approximation formula of Dalal and Wilkinson, valid for pvalues < 0.1. If the pvalue is larger than 0.1, then the result of table is returned ‘table’ uses the table from Dalal and Wilkinson, which is available for pvalues between 0.001 and 0.2, and the formula of Lilliefors for large n (n>900). Values in the table are linearly interpolated. Values outside the range will be returned as bounds, 0.2 for large and 0.001 for small pvalues.
Returns: ksstat : float
Kolmogorov-Smirnov test statistic with estimated mean and variance.
pvalue : float
If the pvalue is lower than some threshold, e.g. 0.05, then we can reject the Null hypothesis that the sample comes from a normal distribution
Notes
Reported power to distinguish normal from some other distributions is lower than with the Anderson-Darling test.
could be vectorized
statsmodels.stats.diagnostic.
lilliefors
(x, pvalmethod='approx')
# -*- coding: utf-8 -*-
'''
样本量必须大于等于20
UserWarning: kurtosistest only valid for n>=20
'''
import numpy
from numpy import random
from statsmodels.stats.diagnostic import lillifors
d = numpy.random.normal(size=200)
n = lillifors(d)
print (n)
'''
(0.047470987201221337, 0.3052490552871156)
'''
Kolmogorov-Smirnov(Kolmogorov-Smirnov) test
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kstest.html#scipy.stats.kstest
- the Kolmogorov-Smirnov(Kolmogorov-Smirnov) test should only be used for large sample numbers (>300)
# -*- coding: utf-8 -*-
'''
样本量必须大于等于20
UserWarning: kurtosistest only valid for n>=20
'''
import numpy
from numpy import random
from scipy import stats
d = numpy.random.normal(size=1000)
n = stats.kstest(d,'norm')
print (n)
'''
KstestResult(statistic=0.028620435047503723, pvalue=0.38131540630243177)
'''
http://jingyan.baidu.com/article/86112f135cf84c27379787cb.html
K-S检验是以两位苏联数学家Kolmogorov和Smirnov的名字命名的,它是一个拟合优度检验。K-S检验通过对两个分布之间的差异的分析,判断样本的观察结果是否来自制定分布的总体。
-
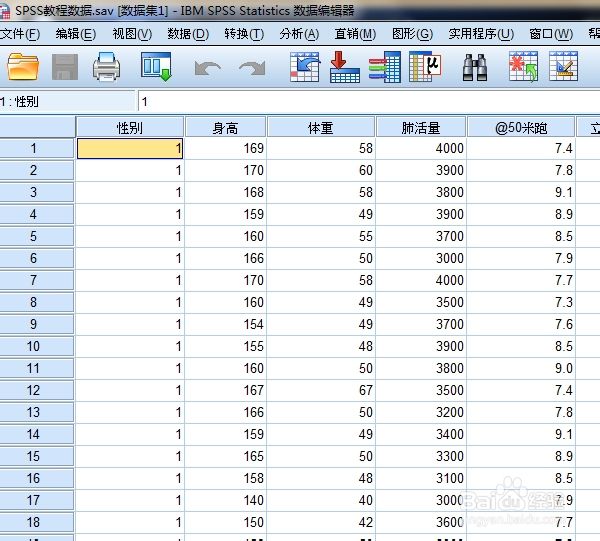
数据录入
首先把要分析的数据导入到SPSS软件中,如图所示:
-
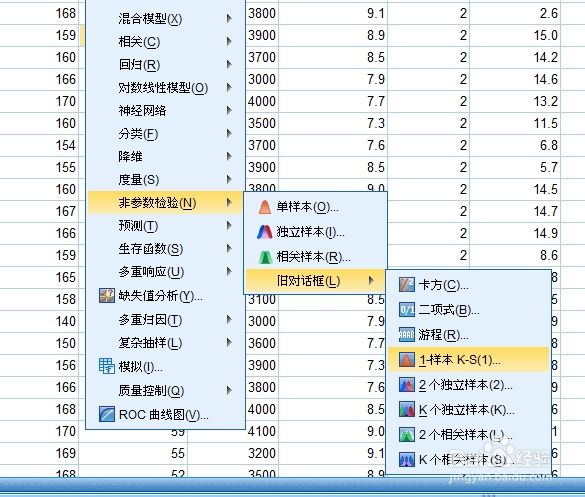
步骤1
点击“分析”,然后选择“非参数检验(N)”,选择“旧对话框”中的“1-样本K-S(1)”,如图所示。
-
步骤2
这里,我们只对“身高”和“体重”进行检验,所以把两变量导入到“检验变量列表(T)”,如图所示。
-
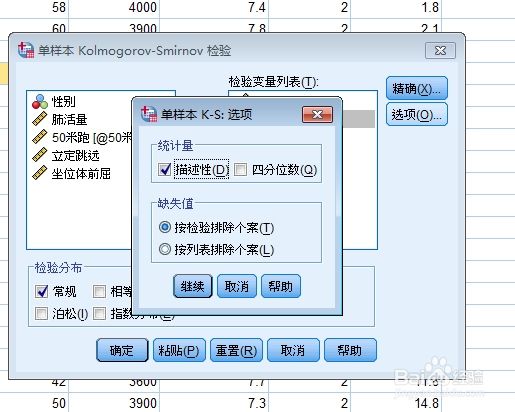
步骤3
然后点击“选项”,选择“描述性(D)”,点击“继续”。如图所示。
-
结果分析
点击“确定”,即可得到以下结果。
由于身高和体重的双侧显著性取值均小于0.10,故否定零假设,即认为初中生的身高和体重不服从正态分布。
柯尔莫哥洛夫-斯米尔诺夫检验(Колмогоров-Смирнов检验)基于累计分布函数,用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。
在进行 cumulative probability统计(如下图)的时候,你怎么知道组之间是否有显著性差异?有人首先想到单因素方差分析或双尾检验(2 tailed TEST)。其实这些是不准确的,最好采用Kolmogorov-Smirnov test(柯尔莫诺夫-斯米尔诺夫检验)来分析变量是否符合某种分布或比较两组之间有无显著性差异。
在统计学中,柯尔莫可洛夫-斯米洛夫检验基于累计分布函数,用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。
在进行累计概率(cumulative probability)统计的时候,你怎么知道组之间是否有显著性差异?有人首先想到单因素方差分析或双尾检验(2 tailedTEST)。其实这些是不准确的,最好采用Kolmogorov-Smirnov test(柯尔莫诺夫-斯米尔诺夫检验)来分析变量是否符合某种分布或比较两组之间有无显著性差异。
分类:
1、Single sample Kolmogorov-Smirnov goodness-of-fit hypothesis test.
采用柯尔莫诺夫-斯米尔诺夫检验来分析变量是否符合某种分布,可以检验的分布有正态分布、均匀分布、Poission分布和指数分布。指令如下:
>> H = KSTEST(X,CDF,ALPHA,TAIL) % X为待检测样本,CDF可选:如果空缺,则默认为检测标准正态分布;
如果填写两列的矩阵,第一列是x的可能的值,第二列是相应的假设累计概率分布函数的值G(x)。ALPHA是显著性水平(默认0.05)。TAIL是表示检验的类型(默认unequal,不平衡)。还有larger,smaller可以选择。
如果,H=1 则否定无效假设; H=0,不否定无效假设(在alpha水平上)
例如,
x = -2:1:4
x =
-2 -1 0 1 2 3 4
[h,p,k,c] = kstest(x,[],0.05,0)
h =
0
p =
0.13632
k =
0.41277
c =
0.48342
The test fails to reject the null hypothesis that the values come from a standard normal distribution.
2、Two-sample Kolmogorov-Smirnov test
检验两个数据向量之间的分布的。
>>[h,p,ks2stat] = kstest2(x1,x2,alpha,tail)
% x1,x2都为向量,ALPHA是显著性水平(默认0.05)。TAIL是表示检验的类型(默认unequal,不平衡)。
例如,x = -1:1:5
y = randn(20,1);
[h,p,k] = kstest2(x,y)
h =
0
p =
0.0774
k =
0.5214
Kolmogorov–Smirnov test (K–S test)
wiki翻译起来太麻烦,还有可能曲解本意,最好看原版解释。
In statistics, the Kolmogorov–Smirnov test (K–S test) is a form of minimum distance estimation used as a nonparametric test of equality of one-dimensional probability distributions used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). The Kolmogorov–Smirnov statistic quantifies a distance between theempirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distribution of this statistic is calculated under the null hypothesis that the samples are drawn from the same distribution (in the two-sample case) or that the sample is drawn from the reference distribution (in the one-sample case). In each case, the distributions considered under the null hypothesis are continuous distributions but are otherwise unrestricted.
The two-sample KS test is one of the most useful and general nonparametric methods for comparing two samples, as it is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.
The Kolmogorov–Smirnov test can be modified to serve as a goodness of fit test. In the special case of testing for normality of the distribution, samples are standardized and compared with a standard normal distribution. This is equivalent to setting the mean and variance of the reference distribution equal to the sample estimates, and it is known that using the sample to modify the null hypothesis reduces the power of a test. Correcting for this bias leads to theLilliefors test. However, even Lilliefors' modification is less powerful than the Shapiro–Wilk test or Anderson–Darling test for testing normality.[1]
python风控评分卡建模和风控常识
https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share
![]()