十进制系统
十进制系统即The Decimal System
在日常生活中，我们每天都在使用逢十进一的数位（0、1、2、3、4、5、6、7、8、9）来表示数字，这种数制叫做十进制。
考察数字83的意义，可以表示成：
83 = (8 × 10) + 3
即八个10再加上一个3；
考察数字4728的意义，可以表示成：
4728 = (4 × 1000) + (7 × 100) + (2 × 10) + 8
即四个1000加上七个100再加上两个10再加上一个8。
从上得知，我们可以说，十进制的基数（base/radix）为10。也即，十进制数是由每个数位的数字乘以10的n次幂，n与数位的位置相关。例如：
83 = (8 × 101) + (3 × 100)
83是由两个数位构成，最左边的数位为最高（有效）数位，这里是8；最右边的数位是最低（有效）数位，这里是3。最低数位的位置所对应的10的幂为0，从右往左依次加一。即，数位3为最低数位，故其10的幂为0，表示为3×100；往左移动一位，数位为8，其10的幂为1，表示为8×101，将所有数位相加得到的和即该十进制数，也即，8×101+ 3×100= 83
使用同样的方法拆解数字4728，表示如下：
4728 = (4 × 103) + (7 × 102) + (2 × 101) + (8 × 02)
我们使用同样的方法表示小数部分，只不过小数部分数位的10的幂为负数。其最大的数位的10的幂为-1，从左向右其数位的10的幂依次减1。例如：
0.256 = (2 × 10-1) + (5 × 10-2) + (6 × 10-3)
在一个既有整数部分又有小数部分的十进制数中，其数位的10的幂也既有正数又有负数：
442.256 = (4 × 102) + (4 × 101) + (2 × 100) + (2 × 10-1) + (5 × 10-2) + (6 × 10-3)
使用表格表示上述数字的数位位置和其10的幂的关系：
| 4 | 7 | 2 | 2 | 5 | 6 |
|---|---|---|---|---|---|
| 百位 | 十位 | 个位 | 十分位 | 百分位 | 千分位 |
| 102 | 101 | 100 | 10-1 | 10-2 | 10-3 |
| position 2 | position 1 | position 0 | position -1 | position -2 | position -3 |
一般的，十进制数使用X来表示：
$$X = \{...d_2d_1d_0d_{-1}d_{-2}d_{-3}...\}$$
X的值为：
$$X=\sum_{i}(d_i×10^i)$$
按位计数系统
按位计数系统即Positional Number Systems
十进制系统是按位计数系统的一种。
在一个按位计数系统中，每个数字（Number）的数位（Digit）的位置使用i表示，数位的权用ri表示。其中，r为数字的基数（base/radix）。
一般的，在该系统中，一个数字可表示为：
$$(...a_3a_2a_1a_0a_{-1}a_{-2}a_{-3}...)_r$$
其中，每一个数位ai都是一个整数，且0≤ai≤r
该数字的值为：
$$ ... + a_3r^3 + a_2r^2 + a_1r^1 + a_0r^0 + a_{-1}r^{-1} + a_{-2}r^{-2} + a_{-3}r^{-3} + ... = \sum_i(a_i × r^i) $$
二进制系统
二进制系统即The Binary System
在十进制系统中，每个数位有十个数可以表示，即0~9。在二进制系统中，每个数位只有0或者1这两个数来表示。
为了避免在表达过程中引起的数制概念混乱，我们给每个数字加上数制下标。例如，十进制数83和4728，我们使用8310和472810表示。
二进制数中的1和0在十进制中的意义相同：
02 = 010
12 = 110
如果要使用二进制数字表示十进制数字中更大的数字（>2），明显的，在二进制中则需要进位了：
$$ 10_2 = (1 × 2^1) + (0 × 2^0) = 2_{10} \\ 11_2 = (1 × 2^1) + (1 × 2^0) = 3_{10} \\ 100_2 = (1 × 2^2) + (0 × 2^1) + (0 × 2^0) = 4_{10} $$
小数部分依然使用10的负次幂表示，这里不再举例。
一般的，使用二进制表示数字：
$$ Y = \{...b_2b_1b_0b_{-1}b_{-2}b_{-3}...\} $$
则Y的值为：
$$ Y = \sum_i(b_i × 2^i) $$
二进制和十进制的转换
将二进制数转换为十进制数非常容易，上述的笔记中已经有很多例子。
而要将十进制数字转换为二进制数字，整数部分和小数部分则需要分开处理。
整数部分
如上述笔记所叙，在二进制中，整数部分可表示为：
$$ b_{m-1}b_{m-2}...b_2b_1b_0\quad(b_i=0或1) $$
该数字的值为：
$$ (b_{m-1} × 2^{m-1}) + (b_{m-2} × 2^{m-2}) + ... + (b_1 × 2^1) + b_0 $$
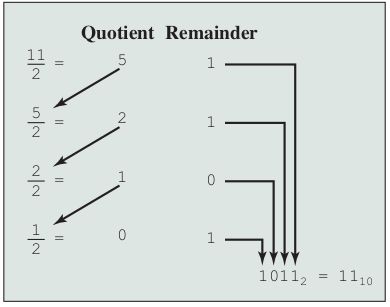
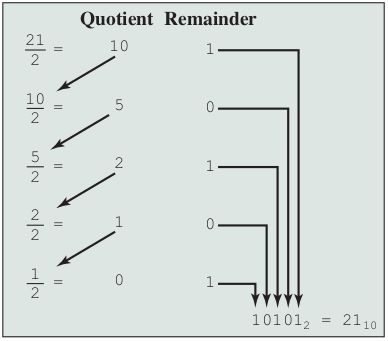
假设我们需要将十进制的整数N转换为二进制，可以将N除以2，将得到一个商N1和余数R0，记为：
$$ N = 2 × N_1 + R_0\quad(R_0=0或1) $$
接着，我们将商N1继续除以2。令其新的商记为N2，新的余数记为R1，则：
$$ N_1 = 2 × N_2 + R_1\quad(R_1=0或1) $$
那么有：
$$ N = 2(2N_2 + R_1) + R_0 = (N_2 × 2^2) + (R_1 × 2^1) + R_0 $$
我们可以将得到的商继续往下除以2，由于N > N1 > N2...，最终会得到商：Nm-1 = 1（010和110除外）以及余数Rm-2 = 0或1，那么我们可以得到：
$$ N = (1 × 2^{m-1}) + (R_{m-2} × 2^{m-2}) + ... + (R_2 × 2^2) + (R_1 × 2^1) + R_0 $$
即N的二进制形式。
因此，将十进制数的整数部分转换为二进制数，只需将数字不断除以2即可，将得到的余数（非0即1）逆序排列，就得到了二进制的整数部分。
例1：将1110转换为二进制。
解：
例2：将2110转换为二进制。
解：
小数部分
如上述笔记所叙，在二进制中，整数部分可表示为：
$$ b_{-1}b_{-2}b_{-3}...\quad(b_i=0或1) $$
该数字的值为：
$$ (b_{-1} × 2^{-1}) + (b_{-2} × 2^{-2}) + (b_{-3} × 2^{-3})... $$
也可以记为：
$$ 2_{-1} × (b_{-1} × 2^{-1} × (b_{-2} × 2^{-1} × (b_{-3} + ...)...)) $$
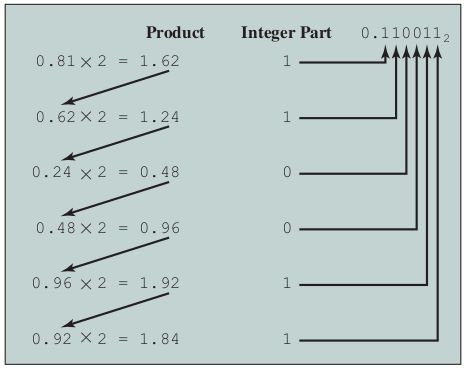
上一个表达式正好提供了一个转换的思路。假设我们要将数字F(0＜F＜1)由十进制转换为二进制。由上可知，数字F可以表示为：
$$ F = 2^{-1} × (b_{-1} + 2^{-1} × (b_{-2} + 2^{-1} × (b_{-3} + ...)...)) $$
等式两边同乘以2得：
$$ 2F = b_{-1} + 2^{-1} × (b_{-2} + 2^{-1} × (b_{-3} + ...)...) $$
由于0＜F＜1，显然的，2F的整数部分b-1∈{0, 1}。我们将剩余的小数部分记为F1，且0＜F1＜1，可得：
$$ F_1 = 2^{-1} × (b_{-2} + 2^{-1} × (b_{-3} + ...)...) $$
为了求b-1，我们可重复上述步骤。以此类推，小数部分的转换算法即将小数不断乘以2即可。算法中每一步的被乘数都是上一步的积的小数部分，且积的整数部分一定是0或1，其构成之正序序列即二进制的小数部分。然而，这个算法是不精确的，因为该算法的精确停止条件是直到积的小数部分等于0为止，而有时该算法可能会一直循环下去。因此，我们需要另一个停止条件：将算法运行到我们所需要的一定精度即可。
例1：将0.8110转换为二进制。
解：
例2：将0.2510转换为二进制。
解：