单目标:鹅优化算法

一、简介

鹅优化算法（GOOSE Algorithm，GO）是2024年由Rebwar Khalid Hamad提出的一种群智能优化算法，该成果发表在知名SCI期刊JCQ3区 Evolving Systems 上。这是一种基于鹅的休息和觅食行为的新型元启发式算法。

二、仿生学原理

1.鹅的休息行为

鹅休息时会成群聚集，其中一只用单腿保持平衡，守护群体。并且偶尔这只守护鹅会抬起一条腿，扛起一块小石头，睡着时石头掉落它就会醒来。

2.鹅的预警行为

当鹅听到任何奇怪的声音或动作时，它们会发出响亮的声音来唤醒群中的个体，并保证它们的安全，在种群中营造一种有吸引力的保护氛围。

三、数理原理

1. 开发阶段

开发阶段模拟守护鹅的行为机制。首先需要估计鹅脚里石头的重量，其重量在5到25公斤之间，通过特定公式可以在任意迭代中随机求出石头的重量，该变量指示迭代的次数。接着，要找到当石头落下时到达地球所需的时间t，它是随机的，取值范围在1到循环中每次迭代的维数之间。之后，计算物体撞击地面并发出声音并传递给群中每只鹅的时间 T。再找出声音在整个迭代过程中传播并到达群中单个鹅所需的总时间，将维度除以总时间量，为了得到所需的平均时间，将总时间除以2。有一个随机变量负责开发和探索阶段的分布，值在(0,1)范围内随机选取。

2. 探索阶段

探索阶段模拟鹅群在觅食等活动中的随机搜索行为。通过一些随机因素和规则，使得鹅个体能够在更大的解空间中进行搜索，避免陷入局部最优解。例如，在某些情况下，鹅个体可能会远离当前的群体位置，去探索新的区域，寻找可能存在的更好的“食物源”（对应优化问题中的更优解）。

四、实现步骤

1.初始化鹅群体

在解空间中随机生成若干个鹅个体，每个个体代表优化问题的一个潜在解。这些初始解构成了算法搜索的起点。

2.评估适应度

根据目标函数对每个鹅个体进行适应度评估。目标函数是衡量解优劣的标准，适应度值越高（或越低，根据具体问题）表示该解越接近最优解。

3.更新位置

通过模仿鹅群体的行为，如觅食和迁徙等，更新每个个体的位置。这一步是算法的核心，通过特定的规则和公式，依据鹅个体当前的位置、群体中其他个体的位置以及一些随机因素，来决定每个个体下一步的移动方向和距离。

4.选择最优解

在更新过程中，保留适应度最高的个体，作为当前最优解。随着迭代的进行，这个最优解会不断进化，逐渐接近全局最优解。

5.终止条件

根据设定的终止条件（如迭代次数达到上限或适应度阈值满足要求），决定是否停止优化。当满足终止条件时，算法输出当前找到的最优解。

五、鹅优化算法的优点

1.收敛速度快

鹅优化算法通过独特的行为模拟机制，能够快速地缩小搜索范围，向最优解靠近。在开发阶段，对守护鹅行为的模拟使得算法能够集中精力在当前可能存在最优解的区域进行搜索；在探索阶段，随机搜索行为也有助于快速发现新的潜在区域，避免陷入局部最优。

2.求解精度高

通过不断地更新个体位置和选择最优解，该算法能够在复杂的解空间中找到精度较高的最优解。其对鹅群体行为的细致模拟，使得算法在搜索过程中能够充分利用群体的信息，从而提高求解的准确性。

六、鹅优化算法的应用

1.工程优化
在焊接梁设计、经济负荷分配问题、压力容器设计问题等工程领域，鹅优化算法都能发挥作用。通过对这些实际问题进行建模，将其转化为优化问题，利用鹅优化算法寻找最优的设计参数或分配方案，以达到提高产品性能、降低成本等目的。

2.神经网络优化

可以用于优化神经网络的参数，如优化RBF神经网络的扩散速度相关参数、优化BP神经网络用于回归预测等。通过优化神经网络的参数，能够提高神经网络的性能，如提高函数逼近能力、加快训练速度、增强泛化能力等。

八、结论

有博主将GOOSE算法在多个知名的基准测试函数上进行了基准测试，包括19个知名的基准测试函数、10个现代基准函数以及5个经典基准函数。并分别与遗传算法(GA)、粒子群算法(PSO)、蜻蜓算法(DA)、适应度依赖优化器(FDO)、鲸鱼优化算法(WOA)、salp swarm算法(SSA)、蝴蝶优化算法(BOA)、黑猩猩优化算法(ChOA)等多种算法进行了对比研究。所取得的结果证明，与目前研究中使用的其他算法相比，鹅优化算法具有优越的性能。

鹅优化算法作为一种新型的群智能优化算法，凭借其独特的灵感来源、有效的搜索机制、良好的性能特点以及广泛的应用前景，在优化算法领域展现出了巨大的潜力，为解决各种复杂的优化问题提供了新的有力工具。

clc;

clear;

close all;

% Change these details with respect to your problem

sums=0;

avgs=0;

for i=1:30    

SearchAgents_no=10;            % Number of search agents

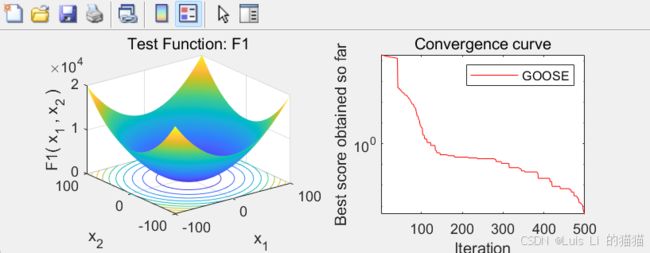
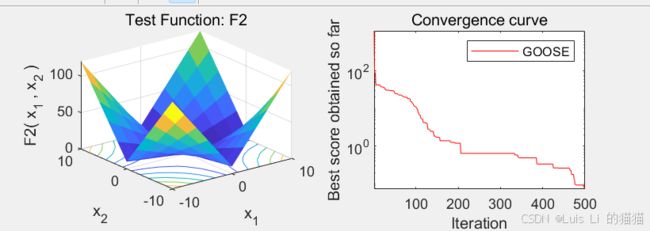
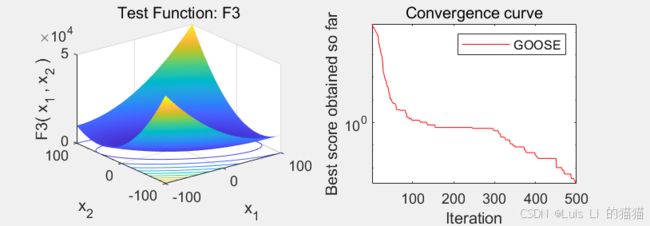
Function_name='F1';            % Name of the test function that can be chnage..

Max_IT=500;                    % Maximum number of iterations

% Load details of the selected benchmark function

[lb,ub,dim,fobj]=Get_Functions_details(Function_name);           %where lb is the lower bound of variable, ub is the upper bound of variable and dim is the number of dimension

[Best_score,Best_pos,Cong_Curve]=GOOSE(SearchAgents_no,Max_IT,lb,ub,dim,fobj);

display( num2str(Best_score));      

sums=sums+Best_score;

end

avgs=sums/30;

[avgs]

display( num2str(avgs));

% Draw chart

figure('Position',[400 400 560 190])

%Draw search space

subplot(1,2,1);

func_plot(Function_name);

title(['Test Function: ',Function_name])

xlabel('x_1');

ylabel('x_2');

zlabel([Function_name,'( x_1 , x_2 )'])

grid on

%Draw objective space

subplot(1,2,2);

semilogy(Cong_Curve,'Color','r')

title('Convergence curve')

xlabel('Iteration');

ylabel('Best score obtained so far');

axis tight

grid off

box on

legend('GOOSE')

鹅优化算法求解

function [Best_score,Best_pos,Cong_Curve]=GOOSE(SearchAgents_no,Max_IT,lb,ub,dim,fobj)

Best_pos=zeros(1,dim);

Best_score=inf;                          %change this to -inf for maximization problems

M_T=inf;

Cong_Curve=zeros(1,Max_IT);

%Initialize the positions of search agents

X=initialization(SearchAgents_no,dim,ub,lb);

Distance_Goose=zeros(SearchAgents_no,dim);

loop=0;                                               % Loop counter

% Main loop

while loop

   for i=1:size(X,1)  

      % Return back the search agents that go beyond the boundaries of the search space

       Flag4ub=X(i,:)>ub;

       Flag4lb=X(i,:)

       X(i,:)=(X(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;              

       % Calculate objective function for each search agent

       fitness=fobj(X(i,:));

           if fitness

              Best_score=fitness;          

              Best_pos=X(i,:);                          

           end

           end    

   for i=1:size(X,1)        

       pro=rand;

     rnd=rand;

      coe=rand();

      if(coe<=0.17)

          coe;

      else

          coe=0.17;

      end

     S_W(i,:)=randi([5,25],1,1);                                         %Eq.(3.1)

     % Time of Arrive object to earth.

     T_o_A_O(i,:)=rand(1,dim);                                           %Eq.(3.2)

     % Time of Arrive Sound to Groups

     T_o_A_S(i,:)=rand(1,dim);                                           %Eq.(3.3)        

     T_T=sum(T_o_A_S(i,:))/dim;                                          %Eq.(3.4)

     % Determine Time Average

     T_A=T_T/2;                                                          %Eq.(3.5)

     if rnd>=0.5

         if pro>0.2              

                 if S_W>=12

                       %  Calculate Free Fall Speed

                       F_F_S=T_o_A_O(i,:) *(sqrt(S_W(i,:))/ 9.81);       %Eq.(3.6)  

                       S_S=343.2;

                       D_S_T(i,:)=S_S* T_o_A_S(i,:);                     %Eq.(3.7)

                       D_G(i,:)=0.5* D_S_T(i,:);                         %Eq.(3.8)

                     X(i,:)=F_F_S + D_G(i,:)* T_A^2;                     %Eq.(3.9)

                   elseif S_W<12

            elseif pro<=0.2

                       %  Calculate Free Fall Speed

                       F_F_S=T_o_A_O(i,:) *(S_W(i,:)/ 9.81);             %Eq.(3.10)

                       S_S=343.2;

                       D_S_T(i,:)=S_S* T_o_A_S(i,:);                     %Eq.(3.7)

                       D_G(i,:)=0.5* D_S_T(i,:);                         %Eq.(3.8)

                     X(i,:)=F_F_S.*D_G(i,:)* T_A^2*coe;                  %Eq.(3.11)          

                    end

             end

                    else

                       if M_T>T_T

                         M_T=T_T;

                       end

                    alpha=(2-(loop/(Max_IT/2)));                         %Eq.(3.12)

                    %random an awakening

                    % exploring wakeup without holding stone.

                    X(i,:)=randn(1,dim).*(M_T*alpha)+Best_pos;           %Eq.(3.13)

       end

   end

   loop=loop+1;

   Cong_Curve(loop)=Best_score;

end

适应度函数

function [lb,ub,dim,fobj] = Get_Functions_details(F)

switch F

   case 'F1'

       fobj = @F1;

       lb=-100;

       ub=100;

       dim=30;

   case 'F2'

       fobj = @F2;

       lb=-10;

       ub=10;

       dim=30;

   case 'F3'

       fobj = @F3;

       lb=-100;

       ub=100;

       dim=30;

end

end

% F1

function o = F1(x)

o=sum(x.^2);

end

% F2

function o = F2(x)

o=sum(abs(x))+prod(abs(x));

end

% F3

function o = F3(x)

dim=size(x,2);

o=0;

for i=1:dim

   o=o+sum(x(1:i))^2;

end

end

绘图函数

function func_plot(func_name)

[lb,ub,dim,fobj]=Get_Functions_details(func_name);

switch func_name 

    case 'F1' 

        x=-100:2:100; y=x; %[-100,100]

    case 'F2' 

        x=-100:2:100; y=x; %[-10,10]

    case 'F3' 

        x=-100:2:100; y=x; %[-100,100]

end    

L=length(x);

f=[];

for i=1:L

    for j=1:L

        if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0

            f(i,j)=fobj([x(i),y(j)]);

        end

        if strcmp(func_name,'F15')==1

            f(i,j)=fobj([x(i),y(j),0,0]);

        end

        if strcmp(func_name,'F19')==1

            f(i,j)=fobj([x(i),y(j),0]);

        end

        if strcmp(func_name,'F20')==1

            f(i,j)=fobj([x(i),y(j),0,0,0,0]);

        end       

        if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1

            f(i,j)=fobj([x(i),y(j),0,0]);

        end          

    end

end

surfc(x,y,f,'LineStyle','none');

end

 （出处：Hamad, R.K., Rashid, T.A. GOOSE algorithm: a powerful optimization tool for real-world engineering challenges and beyond. Evolving Systems (2024). https://doi.org/10.1007/s12530-023-09553-6）