理解Silverlight的路径填充规则

这个可以扩展到矢量图中路径的填充规则，因为所有矢量图都采用这个规则来填充封闭路径的内部，在这里只以Silverlight为例。

在网上找了很久关于填充规则的介绍，经过了几天的阅读和自己理解还有亲自尝试，现在终于能说出过所以然来了，立马分享给大家。

 

矢量路径的填充规则有两种方式，EvenOdd 和 NonZero，下面是我自己总结的中文解释（挺拗口的）。

 

EvenOdd 方式是指从路径内部到外部经过了与路径有偶数个交叉点的那些点被认为在路径之外，有奇数个交叉点的那些点被认为在路径之内并且会被填充。

 

NonZero 方式是指从路径内部到外部经过的那些路径中从左到右和从右到左的数量不相同(差不为0)的那些点会被填充。

 

事实上并没有那么复杂，来看一个实际的例子吧：

 

1 < Path  Fill ="Yellow"
2   Stroke ="Blue"  StrokeThickness ="3"
3   Data ="F1 M 420,200 L 750,200 L 460,300 L 650,100 L 550,350 L 450,150 L 700,350 L 550,150 Z"
4 />

 

 运行之后的图形如下，顶点作了标记：

 

 

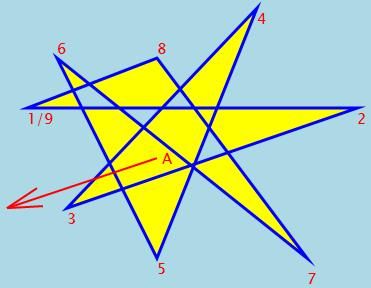
注意上图是NonZero填充。图中A点向外部可以看出经过了2个从左到右（3->4, 5->6，这里方向是从1到9。你也可以从9到1算方向）的路径，但没经过从右到左的路径，所以这两个值的差不为0，所以A点应该被填充。

 

下面是默认的EvenOdd填充效果：

 

 

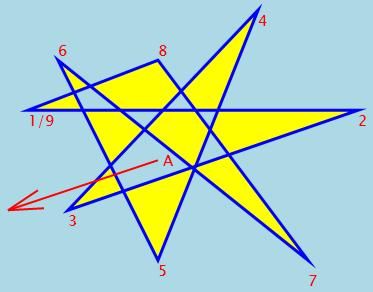
A点向外经过了2个与路径的交叉点，所以被认为在路径之外，所以就不填充。你也可以向反方向画线，但仍然是偶数个交叉点。

 

PS，Path的Data里的命令是区分大小写的，带坐标的命令如果是大写，则用绝对坐标，小写则用相对坐标，要注意噢！