介绍
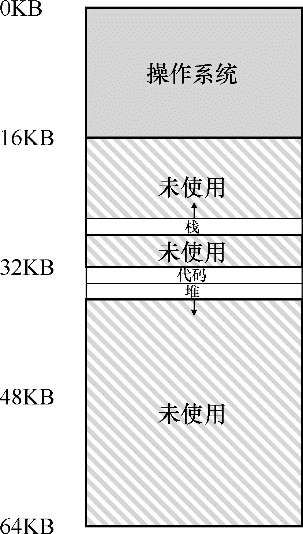
利用基址和界限寄存器,操作系统很容易将不同进程重定位到不同的物理内存区域。但是,对于这些内存区域,栈和堆之间,有一大块“空闲”空间。栈和堆之间的空间并没有被进程使用,却依然占用了实际的物理内存。因此,简单的通过基址寄存器和界限寄存器实现的虚拟内存很浪费。
泛化的基址/界限
为了解决这个问题,分段(segmentation)的概念应运而生。这个想法很简单,在MMU中引入不止一个基址和界限寄存器对,而是给地址空间内的每个逻辑段(segment)一对。一个段只是地址空间里的一个连续定长的区域,在典型的地址空间里有3个逻辑不同的段:代码、栈和堆。分段的机制使得操作系统能够将不同的段放到不同的物理内存区域,从而避免了虚拟地址空间中的未使用部分占用物理内存。
我们来看一个例子,如图所示,64KB的物理内存中放置了3个段。
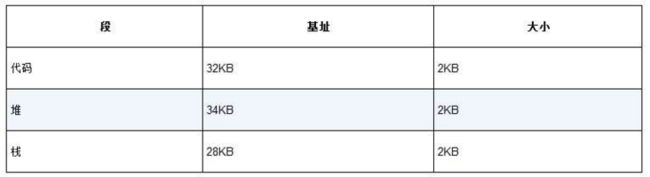
你会想到,需要MMU中的硬件结构来支持分段:在这种情况下,需要一组3对基址和界限寄存器。下表展示了上面的例子中的寄存器值,每个界限寄存器记录了一个段的大小。
引用的是哪个段
硬件在地址转换时使用段寄存器。它如何知道段内的偏移量,以及地址引用了哪个段?
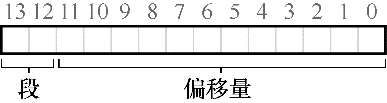
一种常见的方式,有时称为显式(explicit)方式,就是用虚拟地址的开头几位来标识不同的段。在我们之前的例子中,有3个段,因此需要两位来标识。如果我们用14位虚拟地址的前两位来标识,那么虚拟地址如下所示:
前两位告诉硬件我们引用哪个段,剩下的12位是段内偏移。因此,硬件就用前两位来决定使用哪个段寄存器,然后用后12位作为段内偏移。偏移量与基址寄存器相加,硬件就得到了最终的物理地址。请注意,偏移量也简化了对段边界的判断。我们只要检查偏移量是否小于界限,大于界限的为非法地址。
上面使用两位来区分段,但实际只有3个段(代码、堆、栈),因此有一个段的地址空间被浪费。因此有些系统中会将堆和栈当作同一个段,因此只需要一位来做标识。
硬件还有其他方法来决定特定地址在哪个段。在隐式(implicit)方式中,硬件通过地址产生的方式来确定段。例如,如果地址由程序计数器产生(即它是指令获取),那么地址在代码段。如果基于栈或基址指针,它一定在栈段。其他地址则在堆段。
栈的问题
栈和其他的内存段有一点关键区别,就是它反向增长,因此地址转换必须有所不同。首先,我们需要一点硬件支持。除了基址和界限外,硬件还需要知道段的增长方向(用一位区分,比如1代表自小而大增长,0反之)。
支持共享
随着分段机制的不断改进,人们很快意识到,通过再多一点的硬件支持,就能实现新的效率提升。具体来说,要节省内存,有时候在地址空间之间共享(share)某些内存段是有用的。
为了支持共享,需要一些额外的硬件支持,这就是保护位(protection bit)。基本上就是为每个段增加了几个位,标识程序是否能够读写该段,或执行其中的代码。通过将代码段标记为只读,同样的代码可以被多个进程共享,而不用担心破坏隔离。虽然每个进程都认为自己独占这块内存,但操作系统秘密地共享了内存,进程不能修改这些内存,所以假象得以保持。
有了保护位,前面描述的硬件算法也必须改变。除了检查虚拟地址是否越界,硬件还需要检查特定访问是否允许。如果用户进程试图写入只读段,或从非执行段执行指令,硬件会触发异常,让操作系统来处理出错进程。
操作系统支持
分段也带来了一些新的问题。第一个是老问题:操作系统在上下文切换时应该做什么?答案显而易见:各个段寄存器中的内容必须保存和恢复。每个进程都有自己独立的虚拟地址空间,操作系统必须在进程运行前,确保这些寄存器被正确地赋值。
第二个问题更重要,即管理物理内存的空闲空间。新的地址空间被创建时,操作系统需要在物理内存中为它的段找到空间。之前,我们假设所有的地址空间大小相同,物理内存可以被认为是一些槽块,进程可以放进去。现在,每个进程都有一些段,每个段的大小也可能不同。
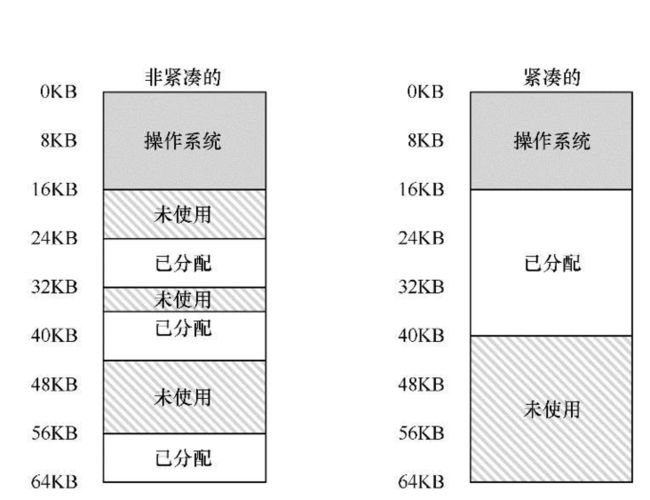
一般会遇到的问题是,物理内存很快充满了许多空闲空间的小洞,因而很难分配给新的段,或扩大已有的段。这种问题被称为外部碎片(external fragmentation)[R69],如图所示。
该问题的一种解决方案是紧凑(compact)物理内存,重新安排原有的段。例如,操作系统先终止运行的进程,将它们的数据复制到连续的内存区域中去,改变它们的段寄存器中的值,指向新的物理地址,从而得到了足够大的连续空闲空间。但是,内存紧凑成本很高,因为拷贝段是内存密集型的,一般会占用大量的处理器时间。
一种更简单的做法是利用空闲列表管理算法,试图保留大的内存块用于分配。相关的算法可能有成百上千种,包括传统的最优匹配(best-fit,从空闲链表中找最接近需要分配空间的空闲块返回)、最坏匹配(worst-fit)、首次匹配(first-fit)以及像伙伴算法(buddy algorithm)这样更复杂的算法。但遗憾的是,无论算法多么精妙,都无法完全消除外部碎片,因此,好的算法只是试图减小它。
空闲空间管理
我们暂且将对虚拟内存的讨论放在一边,先来讨论空闲空间管理(free-space management)的一些问题。在操作系统用分段(segmentation)的方式实现虚拟内存时,以及在用户级的内存分配库(如malloc()和free())中,需要管理的空闲空间由大小不同的单元构成。在这两种情况下,会出现外部碎片的问题,让管理变得较为困难。
假设
首先,我们假定基本的接口就像malloc()和free()提供的那样。具体来说,void * malloc(size t size)需要一个参数size,它是应用程序请求的字节数。函数返回一个指针,指向这样大小的一块空间。对应的函数void free(void *ptr)函数接受一个指针,释放对应的内存块。
进一步假设,我们主要关心的是外部碎片的问题,先将内部碎片问题置之脑后。我们还假设,内存一旦被分配给客户,就不可以被重定位到其他位置。最后我们假设,分配程序所管理的是连续的一块字节区域。
底层机制
分隔与合并
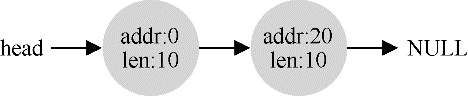
空闲列表包含一组元素,记录了堆中的哪些空间还没有分配。假设有下面的30字节的堆:
这个堆对应的空闲列表如下:
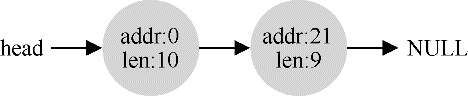
可以看出,任何大于10字节的分配请求都会失败(返回NULL),因为没有足够的连续可用空间。但是,如果申请小于10字节空间,会发生什么?假设我们只申请一个字节的内存,此时分配程序会执行所谓的分割(splitting)动作:它找到一块可以满足请求的空闲空间,将其分割,第一块返回给用户,第二块留在空闲列表中。在我们的例子中,假设这时遇到申请一个字节的请求,分配程序选择使用第二块空闲空间,对malloc()的调用会返回20(1字节分配区域的地址),空闲列表会变成这样:
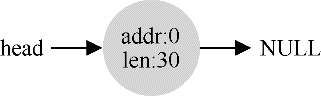
许多分配程序中也有一种机制,名为合并(coalescing)。如果应用程序调用free(10),归还堆中间的空间,会发生什么?分配程序不只是简单地将这块空闲空间加入空闲列表,还会在释放一块内存时合并可用空间。通过合并,最后空闲列表应该像这样:
追踪已分配空间的大小
可以看到,free(void *ptr)接口没有块大小的参数。要完成这个任务,大多数分配程序都会在头结构(header)中保存一点额外的信息,它在内存中的位置通常就在返回的内存块之前。该头块中至少包含所分配空间的大小,它也可能包含一些额外的指针来加速空间释放,包含一个幻数来提供完整性检查,以及其他信息。我们假定,一个简单的头块包含了分配空间的大小和一个幻数:
typedef struct header_t {
int size;
int magic;
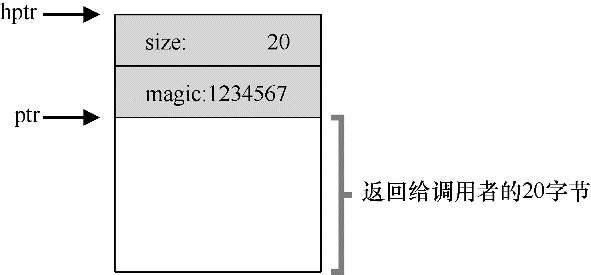
} header_t;在内存中看起来像是这样:
用户调用free(ptr)时,库会通过简单的指针运算得到头块的位置。获得头块的指针后,库可以很容易地确定幻数是否符合预期的值,作为正常性检查(assert(hptr->magic == 1234567)),并简单计算要释放的空间大小(即头块的大小加区域长度)。因此,如果用户请求N字节的内存,库不是寻找大小为N的空闲块,而是寻找N加上头块大小的空闲块。
让堆增长
大多数传统的分配程序会从很小的堆开始,当空间耗尽时,再向操作系统申请更大的空间。通常,这意味着它们进行了某种系统调用(例如,大多数UNIX系统中的sbrk),让堆增长。操作系统在执行sbrk系统调用时,会找到空闲的物理内存页,将它们映射到请求进程的地址空间中去,并返回新的堆的末尾地址。这时,就有了更大的堆,请求就可以成功满足。
基本策略
理想的分配程序可以同时保证快速和碎片最小化。遗憾的是,由于分配及释放的请求序列是任意的,任何策略在某些特定的输入下都会变得非常差。
最优匹配
最优匹配(best fit)策略非常简单:首先遍历整个空闲列表,找到和请求大小一样或更大的空闲块,然后返回这组候选者中最小的一块。最优匹配背后的想法很简单:选择最接近用户请求大小的块,从而尽量避免空间浪费。然而,简单的实现在遍历查找正确的空闲块时,要付出较高的性能代价。
最差匹配
最差匹配(worst fit)方法与最优匹配相反,它尝试找最大的空闲块,分割并满足用户需求后,将剩余的块加入空闲列表。最差匹配尝试在空闲列表中保留较大的块,而不是像最优匹配那样可能剩下很多难以利用的小块。最差匹配同样需要遍历整个空闲列表,大多数研究表明它的表现非常差,导致过量的碎片,同时还有很高的开销。
首次匹配
首次匹配(first fit)策略就是找到第一个足够大的块,将请求的空间返回给用户。首次匹配有速度优势(不需要遍历所有空闲块),但有时会让空闲列表开头的部分有很多小块。因此,分配程序如何管理空闲列表的顺序就变得很重要。一种方式是基于地址排序(address-basedordering),通过保持空闲块按内存地址有序,合并操作会很容易,从而减少了内存碎片。
下次匹配
不同于首次匹配每次都从列表的开始查找,下次匹配(next fit)算法多维护一个指针,指向上一次查找结束的位置。其想法是将对空闲空间的查找操作扩散到整个列表中去,避免对列表开头频繁的分割。这种策略的性能与首次匹配很接近,同样避免了遍历查找。
其他方式
除了上述基本策略外,人们还提出了许多技术和算法,来改进内存分配。
分离空闲列表
它的基本想法很简单:如果某个应用程序经常申请一种(或几种)大小的内存空间,那就用一个独立的列表,只管理这样大小的对象。其他大小的请求都交给更通用的内存分配程序。
这种方法的好处显而易见。通过拿出一部分内存专门满足某种大小的请求,碎片就不再是问题了。而且,由于没有复杂的列表查找过程,这种特定大小的内存分配和释放都很快。
不过这种方式也为系统引入了新的复杂性。例如,应该拿出多少内存来专门为某种大小的请求服务,而将剩余的用来满足一般请求?Solaris系统内核设计的厚块分配程序(slab allocator),很优雅地处理了这个问题。
具体来说,在内核启动时,它为可能频繁请求的内核对象创建一些对象缓存(object cache),如锁和文件系统inode等。这些的对象缓存每个分离了特定大小的空闲列表,因此能够很快地响应内存请求和释放。如果某个缓存中的空闲空间快耗尽时,它就向通用内存分配程序申请一些内存厚块(slab)(总量是页大小和对象大小的公倍数)。相反,如果给定厚块中对象的引用计数变为0,通用的内存分配程序可以从专门的分配程序中回收这些空间,这通常发生在虚拟内存系统需要更多的空间的时候。
厚块分配程序比大多数分离空闲列表做得更多,它将列表中的空闲对象保持在预初始化的状态。数据结构的初始化和销毁的开销很大,通过将空闲对象保持在初始化状态,厚块分配程序避免了频繁的初始化和销毁,从而显著降低了开销。
伙伴系统
因为合并对分配程序很关键,所以人们设计了一些方法,让合并变得简单,一个好例子就是二分伙伴分配程序(binary buddy allocator)。
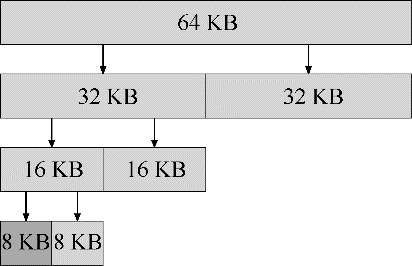
在这种系统中,空闲空间首先从概念上被看成大小为2ⁿ的大空间。当有一个内存分配请求时,空闲空间被递归地一分为二,直到刚好可以满足请求的大小。这时,请求的块被返回给用户。在下面的例子中,一个64KB大小的空闲空间被切分,以便提供7KB的块:
请注意,这种分配策略只允许分配2的整数次幂大小的空闲块,因此会有内部碎片(internal fragment)的麻烦。
伙伴系统的精髓在于内存被释放的时候。如果将这个8KB的块归还给空闲列表,分配程序会检查“伙伴”8KB是否空闲。如果是,就合二为一,变成16KB的块。然后会检查这个16KB块的伙伴是否空闲,如果是,就合并这两块。这个递归合并过程继续上溯,直到合并整个内存区域,或者某一个块的伙伴还没有被释放。
伙伴系统运转良好的原因,在于很容易确定某个块的伙伴。仔细观察的话,就会发现每对互为伙伴的块只有一位不同,正是这一位决定了它们在整个伙伴树中的层次。
其他想法
上面提到的众多方法都有一个重要的问题,缺乏可扩展性(scaling)。具体来说,就是查找列表可能很慢。因此,更先进的分配程序采用更复杂的数据结构来优化这个开销,牺牲简单性来换取性能。例子包括平衡二叉树、伸展树和偏序树。
考虑到现代操作系统通常会有多核,同时会运行多线程的程序,因此人们做了许多工作,提升分配程序在多核系统上的表现。感兴趣的话可以深入阅读glibc分配程序的工作原理。