数学之路(3)-机器学习(3)-机器学习算法-最小二乘法与回归[4]

多元线性回归

一元线性回归是一个主要影响因素作为自变量来解释因变量的变化，在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元性回归。

 

设y为因变量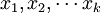，为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

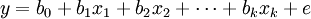
python实现后效果如下：

参数项矩阵为[[ 3.]
 [ 2.]
 [ 1.]]
http://blog.csdn.net/u010255642
3.000000*x1+2.000000*x2+1.000000*x3+-0.000000
>>> 

 

本博客所有内容是原创，未经书面许可，严禁任何形式的转载

http://blog.csdn.net/u010255642

 

 

python代码如下：

 

#!/usr/bin/env python

# -*- coding: utf-8 -*-

#最小二乘法，多变量线性回归

#麦好:[email protected]

#http://blog.csdn.net/u010255642

 

import numpy as np



x =np.matrix([[7,2,3],[3,7,17],[11,3,5]],dtype=np.float64)

y =np.matrix([28,40,44],dtype=np.float64).T

b=(x.T*x).I*x.T*y

print u"参数项矩阵为{0}".format(b)

i=0

cb=[]

while  i<3:

    cb.append(b[i,0])

    i+=1

temp_e=y-x*b

mye=temp_e.sum()/temp_e.size

e=np.matrix([mye,mye,mye]).T

print "http://blog.csdn.net/u010255642"

print "%f*x1+%f*x2+%f*x3+%f"%(cb[0],cb[1],cb[2],mye)

 

多元非线性回归

 

如果自变数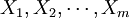与依变数Y皆具非线性关系，或者有的为非线性有的为线性，则选用多元非线性回归方程是恰当的。

（1）一元三次回归方程

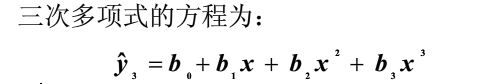
部分python代码如下：

#!/usr/bin/env python

# -*- coding: utf-8 -*-

#最小二乘法，非线性回归,单变量多项式回归

#麦好:[email protected]

#http://blog.csdn.net/u010255642

#y=b1*x+b2*(x^2)+b3*(x^3)

..................

z=np.matrix([3,1.4,1.9]).T

myx =np.matrix([[4],[3],[5]],dtype=np.float64)

x = np.matrix([[myx[0,0],myx[0,0]**2,myx[0,0]**3],\

               [myx[1,0],myx[1,0]**2,myx[0,0]**3],\

               [myx[2,0],myx[2,0]**2,myx[0,0]**3]],\

               dtype=np.float64)

...........

mye=temp_e.sum()/temp_e.size

e=np.matrix([mye,mye,mye]).T

print "http://blog.csdn.net/u010255642"

print "%f*x+%f*x^2+%f*x^3+%f"%(cb[0],cb[1],cb[2],mye)

pltx=np.linspace(0,10,1000)

plty=cb[0]*pltx+cb[1]*(pltx**2)+cb[2]*(pltx**3)+mye

plt.plot(myx,y,"*")

plt.plot(pltx,plty)

plt.show()

 

 

效果:

>>> 

参数项矩阵为[[ 3. ]

 [ 1.4]

 [ 1.9]]

http://blog.csdn.net/u010255642

3.000000*x+1.400000*x^2+1.900000*x^3+0.000000

>>> 

 

(2)二元二次多项式回归方程为：

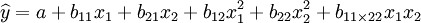
令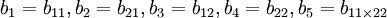,及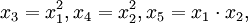于是上式化为五元一次线性回归方程：

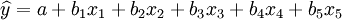
建立二元二次多项式回归方程。

 

 

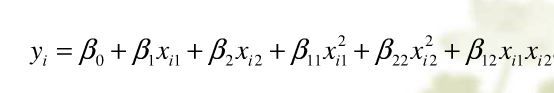
python代码同（1）差不多

执行效果

 

参数项矩阵为[[ 3. ]
 [ 1.4]
 [ 1.9]]
http://blog.csdn.net/u010255642
3.000000*x1+1.400000*x2^2+1.900000*x1*x2+0.000000