前言
没有必要过度关注本文中二叉树的增删改导致的结构改变,规则操作什么的了解一下就好,看不下去就跳过,本文过多的XX树操作图片纯粹是为了作为规则记录,该文章主要目的是增强下个人对各种常用XX树的设计及缘由的了解,也从中了解到常用的实现案例使用XX树实现的原因。
数据在计算机中的存储结构主要为顺序存储结构、链式存储结构、索引存储结构、散列存储结构,其中链式存储结构最常见的示例是链表与树,链式存储结构主要有以下特点:
优点:逻辑相邻的节点物理上不必相邻,插入、删除灵活,只需改变节点中的指针指向
缺点:存储空间利用率低,需通过指针维护节点间的逻辑关系;查找效率比顺序存储慢
度:当前节点下的子节点个数
二叉树
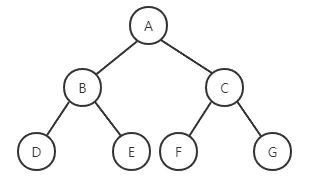
二叉树是每个节点最多有两个子树的树结构,左侧子树节点称为“左子树”(left subtree),右侧子树节点称为“右子树”(right subtree)。每个节点最多有2个子节点的树(即每个定点的度小于3)。
二叉树的特点
至少有一个节点(根节点)
每个节点最多有两颗子树,即每个节点的度小于3。
左子树和右子树是有顺序的,次序不能任意颠倒。
即使树中某节点只有一棵子树,也要区分它是左子树还是右子树。
满二叉树
除了叶子节点外每一个节点都有两个子节点,且所有叶子节点都在二叉树的同一高度上。
完全二叉树
如果二叉树中除去底层节点后为满二叉树,且底层节点依次从左到右分布,则此二叉树被称为完全二叉树。
二叉查找树(Binary Search Tree - BST,又称二叉排序树、二叉搜索树)
二叉查找树根节点的值大于其左子树中任意一个节点的值,小于其右子树中任意一节点的值,且该规则适用于树中的每一个节点。
二叉查找树的查询效率介于O(log n)~O(n)之间,理想的排序情况下查询效率为O(log n),极端情况下BST就是一个链表结构(如下图),此时元素查找的效率相等于链表查询O(n)。
二叉查找树需要注意的是删除节点操作时的不同情况,删除节点根据节点位置会有以下三种情况:
删除节点的度为0,则直接删除
删除节点的度为1,则该子节点替代删除节点
删除节点的度为2,则从左子树中寻找值最大的节点替代删除节点。对树结构改动最少、节点值最进行删除节点值的必然是左子树中的最大叶子节点值与右子树中的最小叶子节点值
为什么不用右子树中的最小叶子节点值取代删除节点?个人认为是为了维持范围值(纯属臆测):
右子树中的最小叶子节点值大于删除节点左子树中的所有节点,但若该叶子节点比删除节点大很多,这将会大大扩大左子树的范围值,左子树可插入的范围值也会大大增大,对左子树的查询效率造成较大的影响 左子树中的最大叶子节点值也大于删除节点左子树中其它所有的节点,虽然是使用该节点替代删除节点会缩小的左子树的值范围,但也减少左子树的插入范围值,对左子树的查询影响不大
由上可以看出,二叉查找树(BST)无法根据节点的结构改变(添加或删除)动态平衡树的排序结构,也因此对某些操作的效率造成一定的影响,而AVL树在BST的结构特点基础上添加了旋转平衡功能解决了这些问题。
平衡二叉搜索树 (Balanced binary search trees,又称AVL树、平衡二叉查找树)
AVL树是最早被发明的自平衡二叉搜索树,树中任一节点的两个子树的高度差最大为1,所以它也被称为高度平衡树,其查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n)。
平衡二叉搜索树由Adelson-Velskii和Landis在1962年提出,因此又被命名为AVL树。平衡因子(平衡系数)是AVL树用于旋转平衡的判断因子,某节点的左子树与右子树的高度(深度)差值即为该节点的平衡因子。
AVL树的特点
具有二叉查找树的特点(左子树任一节点小于父节点,右子树任一节点大于父节点),任何一个节点的左子树与右子树都是平衡二叉树
任一节点的左右子树高度差小于1,即平衡因子为范围为[-1,1] 如上左图根节点平衡因子=1,为AVL树;右图根节点平衡因子=2,固非AVL树,只是BST。
为什么选择AVL树而不是BST?
大多数BST操作(如搜索、最大值、最小值、插入、删除等)的时间复杂度为O(h),其中h是BST的高度。对于极端情况下的二叉树,这些操作的成本可能变为O(n)。如果确保每次插入和删除后树的高度都保持O(log n),则可以保证所有这些操作的效率都是O(log n)。
节点插入、旋转
AVL树插入节点的如下:
根据BST入逻辑将新节点插入树中
从新节点往上遍历检查每个节点的平衡因子,若发现有节点平衡因子不在[-1,1]范围内(即失衡节点u),则通过旋转重新平衡以u为根的子树
旋转的方式:
左旋转:用于平衡RR情况,对失衡节点u(unbalanced)及子树进行左旋
右旋转:用于平衡LL情况,对失衡节点u及子树进行右旋
左右旋转:用于平衡LR情况,对失衡节点失衡u的左子节点ul左旋,再对失衡节点u右旋
右左旋转:用于平衡情况,对失衡节点u失衡方向的右子节点ur右旋,再对失衡节点u左旋
LL - 插入节点是失衡节点u左子节点ul上的左子树节点
gif图中的高度是从叶子节点开始计算的,因为插入节点后是从下往上检测节点的平衡因子,所以叶子节点高度恒为1更方便平衡因子的运算
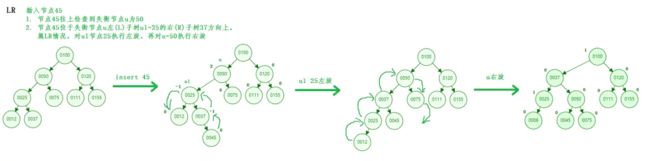
LR - 插入节点是失衡节点u左子节点ul上的右子树节点
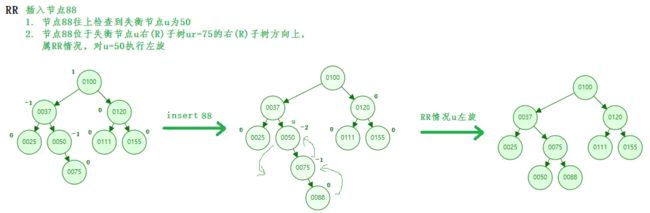
RR - 插入节点是失衡节点u右子节点ur上的右子树节点
RL - 插入节点是失衡节点u右子节点ur上的左子树节点
规律总结:
失衡节点到其最底部叶子节点的高度不会超过4
失衡节点哪里不平衡就会往哪里的反向旋转
添加的节点到失衡节点的路径如果是一条直线(即LL或RR),则只需对失衡节点u进行反向旋转
添加的节点到失衡节点的路径如果是一条曲线(即LR或RL),则需先对该路径上失衡节点u的子节点(ul/ur)进行旋转,再对失衡节点进行旋转
失衡节点u旋转后会成为它原来子树(ul/ur)中的一颗子树,如果u旋转时替代u的子树已有u旋转方向上的子树,那么该子树会断裂成为u的子树(如下LR的u右旋,uls已有右子树T2,故会T2断裂以BST的规则重新插入成为u的子树)
uu uls/\ / \ / \ ulT3 Left Rotate (us) uls T3 Right Rotate(u) ul u/\ - - - - - - - - -> / \ - - - - - - - -> / / \
T1 uls ul T2 T1 T2 T3\ / T2T1 复制代码
节点删除步骤
对删除节点D根据BST规则执行删除
选择平衡,该步骤与插入区别不大,从D节点往上遍历检查每个节点的平衡因子,若发现有节点失衡,则通过旋转重新平衡以u为根的子树
例子:
根据BST规则删除节点133,155替代133位置
从155位置往上检测到100为失衡节点u,左高右低为LR情况,对u左子节点ul=37左旋,再对u节点执行右旋(可以看成对50同时插入2个子节点导致100节点失衡)
AVL树伪代码
红黑树(Red - Black Tree)
红黑树是一种自平衡二叉搜索树(BST),且红黑树节点遵循以下规则:
每个节点只能是红色或黑色
根节点总是黑色的
红色节点的父或子节点都必然是黑色的(两个红色的节点不会相连)
任一节点到其所有后代NULL节点的每条路径都具有相同数量的黑色节点
每个Null节点都是黑色的
相比AVL树
AVL树比红黑树更加平衡,但AVL树可能在插入和删除过程中引起更多旋转。因此,如果应用程序涉及许多频繁的插入和删除操作,则应首选Red Black树(如 Java 1.8中的HashMap)。如果插入和删除操作的频率较低,而搜索操作的频率较高,则AVL树应优先于红黑树。
个人引申的疑问
为什么红黑树也算平衡树呢?它的平衡因子是什么?
为什么AVL比红黑树更平衡?为什么AVL树插入和删除会引起更多选择呢?
原因可从后续的插入步骤与演示案例得出
插入节点
红黑树插入节点后违反的主要规则是两个连续的红色节点。
插入步骤:
将新节点n根据BST规则插入,且新使节点颜色为红色
根据n的父节点p情况执行不同的操作 2.1 n没有父节点p,即N为根,将n的颜色更改为黑色 2.2 p为黑色,直接插入 2.3 p为红色,则根据不同的情况执行操作 2.3.1:n的uncle节点u是红色(uncle节点:父节点p父节点下的另一节点|n祖父节点g的另一子节点) a. 将节点p与节点u改为黑色 b. 将g的颜色改为红色 c. 将祖父节点g当成节点n,对n重复b、c步骤 2.3.2:n的uncle节点n是黑色,则会有以下案例(类同AVL树,g=avl.u,p=avl.ul|ur): LL:p是g左节点,x是p的左节点,对g进行右旋 LR:p是g的左节点,x是p的右节点 RL:p是g的右节点,x是p的右节点 RR:p是g的右节点,x是p的左节点 调整旋转了的节点颜色
检查根节点,根节点为红色则染黑
演示案例
插入12:父节点25是红色节点,uncle节点75是红色节点,属插入的2.3.1情况,将父节点25改为黑色,将祖父节g点改为红色,最后将根节点g即改为黑色
插入35:父节点25是黑节点,属2.2,直接插入
插入42:父节点35是红色节点,uncle节点12是红色节点,属2.3.1,将父节点35改为黑色,祖父节点25改为红色,根节点保持黑色
插入38:父节点42是红色节点,uncle节点是黑色的空节点,属2.3.2,42(p)是35(g)的右节点,38(n)是42的左节点,为RL情况,对42(p=avl.ur)右旋,再对35(g=avl.u)左旋
引申疑问自答
红黑树是根据节点的值与颜色维持平衡的,即可把颜色看成平衡因子,所以即使左右子树的高度差>=2也不一定像AVL树一样为了保持平衡而旋转
AVL树的结构主要是围绕节点值与左右子树高度来保持平衡的,从节点值的角度考虑自然比红黑树更平衡,且值搜索时AVL的效率更高,但插入与删除较多时AVL树旋转操作会比红黑树更多,效率自然更慢
以上也是Java 8的HashMap中树节点实现结构采用红黑树而不是AVL树的原因
删除节点
删除节点主要违反的规则是子树中黑色高度的更改,导致根节点到叶子路径的黑色高度降低。
红黑树删除时一个比较复杂的过程,为了更容易的理解删除过程,可以使用双黑概念去简化理解该过程。 双黑概念指当删除黑色节点后使用了另一个黑色节点替代删除节点的位置(也可以当成有两个null的黑色叶子节点因删除重叠成1个),这也意味着根节点到替代节点的原路径上少了一个黑色节点导致违反了到任一叶子节点路径上含相同的黑色节点数的节点规则(黑色)。当删除时出现双黑情况,则需要通过旋转将节点转换为单黑色(重叠的两个黑色null节点重新铺展为2个)。
删除步骤
执行标准的BST删除,设删除节点为d(delete),替代节点为r(replace)
如果替换节点r或删除节点d其中一个为红色,则将替换节点r标记为黑色(因d是r的父级,红黑树不允许两个连续红色节点),结束删除流程,否则进行步骤3
r和d都是黑色,则按以下步骤进行操作 3.1 将r涂为双黑色(注:如果d是含值叶子节点,那么Null节点替代也是双黑) 3.2 若r不是根节点,设d的同级兄弟节点为b(brother,类似avl.ul|avl.ur),b的父节点为p(parent,类似avl.u),根据以下三种不同的情况进行相应的操作: d兄弟b是黑色,且b至少有1个红色的子节点,则对b进行旋转(规律类同)。设b的红色子节点为r(类似avl的插入节点),根据b和r的位置,可以将这种情况分为四个子情况(LL、LR、RL、RR): LL:b是其父节点(类似avl.u)的左子节点(类似avl.ul),r是b的左子节点或b的两个子节点都是红色,则对p进行右旋 LR:b是其父节点的左子节点(类似avl.ul),r是b的右子节点,则对b进行左旋,再对p进行右旋 RR:b是其父节点的右子节点(类似avl.ur),r是b的右子节点,则对p进行左旋 RL:b是其父节点的右子节点(类似avl.ur),r是b的左子节点,则对b进行右旋,再对p进行左旋 d兄弟b是黑色,且b的子节点都是黑色,则执行重新着色 a. 如果父节点是黑色的,则由父节点开始往下重新着色 b. 如果b父节点p是红色的,则不需要为p之前的节点重新着色,只需将节点p改为黑色(红+双黑=单黑) d兄弟b是红色,则将b向上移动(b左旋或右旋),并为b与父节点重新p着色 如果正常顺序添加上图节点删除节点d的兄弟b只会是黑色,需对其子节点添加一节点再删除添加的节点是可使b变红。 3.3 如果以上操作后u为根,则将其设为黑色,然后返回(完整树的黑色高度减少1)。
B-Tree(B树)
大多数自平衡搜索树(如AVL和红黑树)都会假定所有数据都在主内存中,但我们必须考虑无法容纳在主内存中的大量数据。当键的数量很大时,将以块形式从磁盘读取数据,与主存储器访问时间相比,磁盘访问时间非常高。 B树是一种自平衡搜索树,设计的主要思想是减少磁盘访问次数。大多数树操作(增、删、查、最大值、最小值等)都需要都需要O(h)磁盘访问,h为树的高度。B树通过在节点中放置最大可能的键来保持B树的高度较低。通常,B树节点的大小保持与磁盘块大小相等。由于B树的高度较低,因此与平衡的二叉搜索树(如AVL树、红黑树等)相比,大多数操作的磁盘访问次数显著减少。
磁盘块是一个虚拟的概念, 是操作系统(软件)中最小的逻辑存储单位,操作系统与磁盘打交道的最小单位是磁盘块。
一颗m阶(m指一个节点中最多包含的子节点数)B树特点如下:
所有叶子处于同一水平位置
除根节点外的每个节点都必须至少包含m/2-1个key,并且最多具有m-1个key,除根以外的所有非叶子节点必须至少具有m/2个子节点
节点的子节点数等于节点的key数加1
节点的所有key都按键值升序排序,两个键k1和k2之间的子key包含k1和k2范围内的所有键
与其他平衡二叉搜索树一样,搜索、插入和删除的时间复杂度为O(log n) p.s:B树由术语最小度t定义,t的值取决于磁盘块的大小,数值上m = 2t。
搜索
B-树搜索类似于搜索二叉树,算法与递归算法相似。在B树中,搜索过程也是从根节点开始,通过与节点key值比较进行搜索,搜索操作的时间复杂度为O(log n)。具体的搜索步骤如下:
将搜索值与树中根节点的第一个key进行比较
匹配则显示“找到给定节点”并结束搜索,否则进入步骤3
检查搜索值是大于还是小于当前key值 搜索值小于当前key:左子树中获取第一个key进行比较,重复2、3步骤 搜索值大于当前key:将搜索值与同一节点中的下一个key进行比较,重复2、3步骤,直到精确匹配,或搜索值与叶子节点中的最后一个key值相比较
如果叶节点中的最后一个键值也不匹配,则显示“找不到元素”并结束搜索
插入
设B树的阶为m,则插入流程如下:
如果树为空,则创建一个具有新键值的新节点,并将其作为根节点插入到树中,结束插入流程。
如果树不为空,则从根节点开始根据BST逻辑找到适合添加新键值的节点P,根据节点P的键空间情况(key数量 < m - 1,则key未满)进行不同的操作 2.1 节点P键未满:将新元素由小到大升序排序的方式添加到节点P的key中,结束插入流程 2.2 节点P键已满,则根据P是否为根节点进行相应的操作: a. 节点P非根节点:向父节点插入P的key中间值来拆分节点P(中间值按最小的发送),重复该操作,直到将发送值固定到节点中为止。若发送到根节点使根节点键溢出,则执行步骤b b. 节点P为根节点:根节点P的中间key值将成为树的新根节点,该key左右的key值成为根节点的左右子树,树的高度将增加一
4阶B树插入示例
以下示例皆为4阶B树(m=4),则有以下规则:
4阶B树的每个节点的最多key数目为3,最小key数目为1(m = 4, max_key_num = m - 1 =3, min_key_num = m/2 - 1 =1)
除根节点外的每个节点至少包含2个子节点,最多包含4个子节点(m = 4, min_sub_num = m/2 = 2)
插入流程 2.1 & 2.2.b 示例
插入125(插入流程2.1):根节点P未满,按升序将50插入到P
插入50(插入流程2.2.b):根节点P已满,将最小的中间值100独立为新的根节点,小于100的成为左子树,大于100的成为右子树
插入流程2.2.a 示例
插入115,插入节点后键溢出,取中间值114插入到父节点
根节点key数量溢出,取中间值112成为新的根节点,小于112的key作为112根节点的左子节点,大于112的key作为112根节点的右子节点,原插入节点位置的水平子树成为根节点左右子节点的子节点
删除
B树的删除比插入要复杂得多,因为我们可以从任何节点(不仅是叶子)中删除key,而且从内部节点删除key时,我们将不得不重新排列节点的子节点。 从B树中删除键的各种情况(设删除键k所在节点为n):
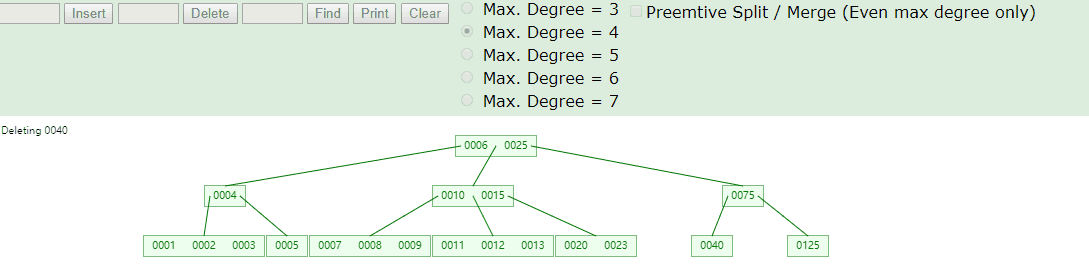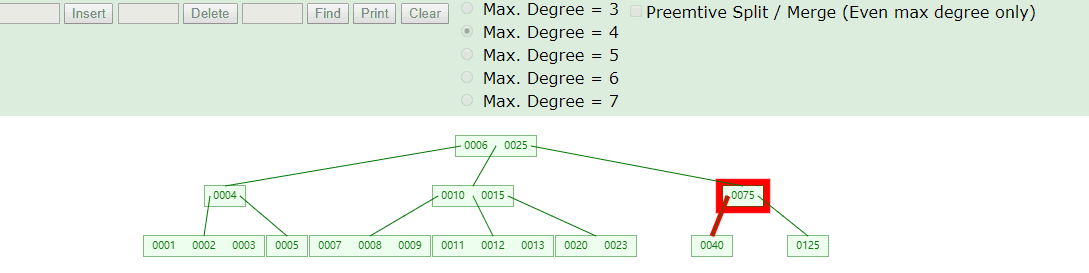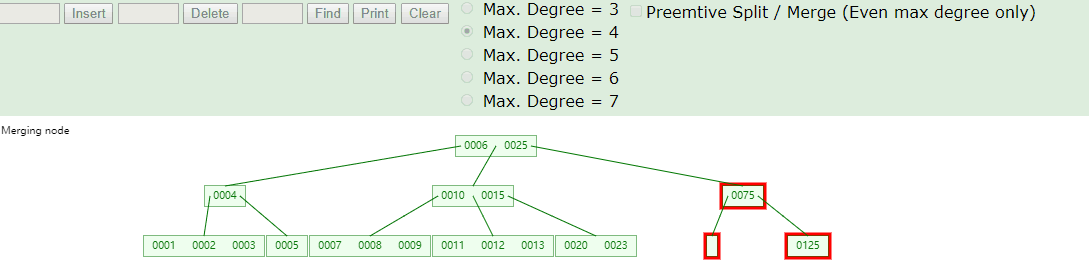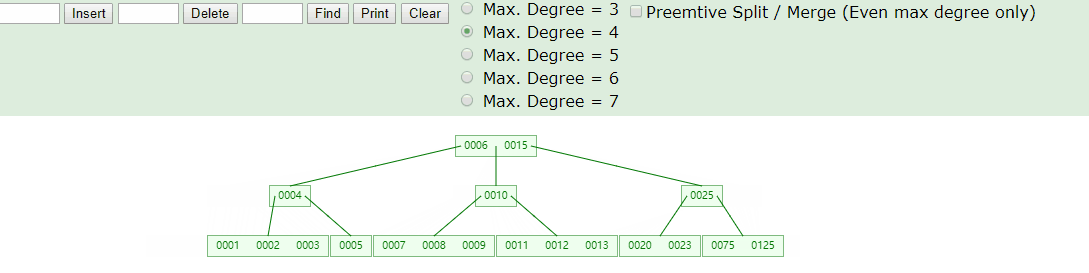
k所在节点n为树中节点(非叶子节点也非根节点),则根据以下不同的情况执行子节点key上移或合并完成删除操作 a. 节点n中在k之前的子节点kln(key left node)键数至少有m/2个,则在kln节点中查找最接近k的键k0,将k0替换k,结束删除操作。图例:m=4, m/2=2 , 删除k=75,k0=55 b. 节点n中在k之前的子节点kln键数少于m/2个,且k后的子节点krn(key的右侧节点)键数至少有m/2个,则在krn节点中查找最接近k的键k0,将k0替换k,结束删除操作。图例:m=4, m/2=2 , 删除k=55,k0=88 c. nkl与nkr键数都少于m/2个,则合并nkl与nkr为一个节点,删除k,结束删除操作。图例:m=4, m/2=2 , 删除k=99, k左侧与右侧子节点都小于m/2=2,合并两个子节点45与100
k所在节点n为叶子节点,则根据叶子节点n的key数是否少于m/2进行不同的删除操作 2.1 n.key数 >= m/2:则直接删除k(B树非根节点需至少包含m/2-1个key),结束删除流程。图例:m=4,m/2=2,删除k=5,所在节点n,key数=2,删除后节点key数为1,符合至少m/2-1个key规则 2.2 n.key数 < m/2 , 即n.key数=m/2 -1:删除key,删除后检查父节点与同父节点的相邻节点key数目进行相应的节点迁移以确保所有节点符合至少m/2-1个key规则,。 2.2.1 n的左侧节点nl.key数 >= m/2:取删除key指向的父节点左侧key下移到删除key位置,从n的左侧节点取最大的key上移到父节点np.key位置 2.2.2 n的左侧节点nl.key数 < m/2且右侧节点nr.key数 >= m/2:取删除key指向的父节点右侧key下移到删除key位置,从n的右侧节点取最小的key上移到父节点np.key位置,相当于2.2.1的镜像操作 2.2.3 nl.key数 < m/2 && nr.key数 < m/2 && np.key数 >= m/2:取删除key指向的父节点左侧key下移到删除key位置,将节点n与nl合并,若n为父节点下的最左侧节点,则n与nr合并。 2.2.4 nl.key数 < m/2 && nr.key数 < m/2 && np.key数 = m/2 -1:最麻烦的一种情况,具体步骤如下。 a. 取删除key指向的父节点np.key下移到删除key位置,将节点n与同父节点np下的相邻节点合并 b. 下移后父节点np.key数必然少于m/2-1,np从其父节点ng获取最接近下移np.key的键ng.key c. ng.key下移后会导致ng与np节点的相连key缺失,根据BST规则父节点的key比np及其子节点下的key值都要大或都要小,从np同父节点ng下的key数>2的相邻节点且npb(先左后右)取靠近np一侧的npb.key替代ng的缺失key;若npg.key数 < m/2,则将npg与n节点合并,结束删除流程,反之进入步骤c d. npb的key上移到ng后同样会使key缺失,n节点合并后也会导致np的子节点缺1,将npb缺失key连接的节点迁移到np缺失的子节点位置。若ng出现与np的情况,则以操作np的方式往上递归操作ng。
B+ Tree(B+树)
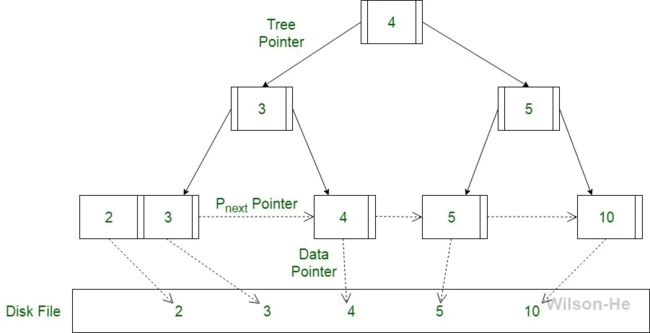
实现动态多级索引时,通常会采用B树和B+树的数据结构。但是,B树有一个缺点是它将与特定键值对应的数据指针(指向包含键值的磁盘文件块的指针)以及该键值存储在B树的节点中。该设计大大减少了可压缩到B树节点中的条目数,从而增加了B树中级别数与记录的搜索时间。 B+树通过仅在树的叶节点处存储数据指针来消除上述B树的缺点,因而B+树的叶节点结构与B树的内部节点结构完全不同。数据指针在B+树中仅存在于叶节点,因此叶节点必须将所有键值及其对应的数据指针存储到磁盘文件块以便访问。此外,叶节点也用于链接以提供对记录的有序访问。因此,叶节点才是第一级索引,而内部节点只是索引到其它级别索引的多层索引。叶节点的一些键值也出现在内部节点中,主要是作为简化搜索记录的一种媒介。 B+树与具有同级的B树相比,具有同级的B+树可以在其内部节点中存储更多键,显着改善对任何给定关键字的搜索时间,同样的键数B+树级别较低且含指向下一个节点的指针P的存在使B+树在从磁盘访问记录时非常快速有效。如设B树与B+树某一级别内部节点都有100K的容量,由于B树的节点除了存键和数据指针,所以实际存的键容量连一半50K可能都没有,但B+树的100K容量都用于存键了,所以索引自然更高效。
B树与B+树的区别:
B树 B+树 所有节点都有数据指针 数据指针集中在叶节点 叶节点不存储为链表结构 叶节点存储为链表结构 并非所有键都在叶节点上,搜索需花费更多时间(重复中序遍历) 所有键都在叶节点上,搜索更快更准确(根据key找到大致叶节点后基于叶节点的链表查询) 树中不会有重复键 键重复出现,且所有key、数据节点都在叶子上 没有多余的搜索键 可能存在冗余搜索键 内部节点的删除非常复杂,并且树必须进行大量转换 删除任何节点都很容易,因为所有节点都可以在叶子上找到 插入会花费更多时间,有时无法预测 插入更容易,结果始终相同
XX树实现案例
数据结构 实现案例 理由 红黑树 JDK 1.8的HashMap HashMap的增删操作多,相比AVL树使用红黑树实现可以减少树的旋转操作 B-Tree MongoDB索引 1. 普通的二叉树或平衡树无法支撑数据库的大数据量(参考B-Tree简介)
2. MongoDB是非关系型聚合数据库,B树恰好将键字段和数据字段聚合在一起,而B+树中的内部节点不存储数据,叶节点间链表连接的优势在MongoDB的JSON数据格式面前也不明显
3. B树所有节点都有数据指针,MongoDB存Mongodb使用B树只要找到指定的索引,就可进行数据访问,避免了叶节点的访问。 B+Tree MySQL索引 关系型数据库最常用的是数据遍历与范围操作,基于B-Tree的设计理由与B-Tree的缺点,B+树所有数据都存储在叶节点中,并且通过指针串在一起,因此很容易进行间隔遍历甚至或遍历
B-Tree缘由:大多数自平衡搜索树(如AVL和红黑树)都会假定所有数据都在主内存中,但我们必须考虑无法容纳在主内存中的大量数据。当键的数量很大时,将以块形式从磁盘读取数据,与主存储器访问时间相比,磁盘访问时间非常高。
结语
搞图搞得最多最耗时的一次笔记如有错误,还请指出。
作者:WilsonHe
链接:https://juejin.im/post/5efc04c7e51d45347c1b6efa
来源:掘金