Android 贝赛尔曲线

版权归作者所有，转发请注明出处：https://www.jianshu.com/p/6f2955dc821d

什么是贝塞尔曲线？

是应用于二维图形应用程序的数学曲线一般在软件开发中我们使用它进行精确的绘制平滑的曲线。

如何绘制一条简单的曲线?

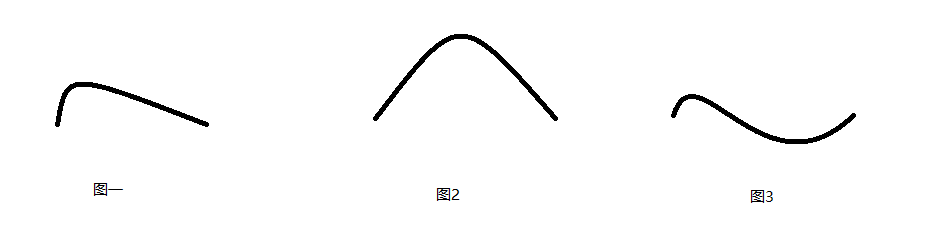
首先我们来看看一些简单的图形

Bizer案例

我们可以看到上面三张图片都是一些比较简单的曲线,那么我们如何使用编程的方式将其是现在界面上了,首先我们对这几张图片进行分析

控制点

我们发现所有曲线都由起始点,控制点(可以有多个),结束点三个部分组成,只要我们能够在显示器上精确的定位这三个部分就能实现曲线的绘制

Android对贝塞尔曲线的支持

在Android中的Path类对贝塞尔曲线进行支持

1 . 对于单个控制点的贝塞尔曲线:

/**
     * Add a quadratic bezier from the last point, approaching control point
     * (x1,y1), and ending at (x2,y2). If no moveTo() call has been made for
     * this contour, the first point is automatically set to (0,0).
     *
     * @param x1 The x-coordinate of the control point on a quadratic curve
     * @param y1 The y-coordinate of the control point on a quadratic curve
     * @param x2 The x-coordinate of the end point on a quadratic curve
     * @param y2 The y-coordinate of the end point on a quadratic curve
     */
    public void quadTo(float x1, float y1, float x2, float y2) {
        isSimplePath = false;
        native_quadTo(mNativePath, x1, y1, x2, y2);
    }

其中起始点为此Path的上一个连接点,x1,y1为此曲线的控制点,x2,y2为结束点

2 . 对于多个控制点的贝塞尔曲线:

/**
     * Add a cubic bezier from the last point, approaching control points
     * (x1,y1) and (x2,y2), and ending at (x3,y3). If no moveTo() call has been
     * made for this contour, the first point is automatically set to (0,0).
     *
     * @param x1 The x-coordinate of the 1st control point on a cubic curve
     * @param y1 The y-coordinate of the 1st control point on a cubic curve
     * @param x2 The x-coordinate of the 2nd control point on a cubic curve
     * @param y2 The y-coordinate of the 2nd control point on a cubic curve
     * @param x3 The x-coordinate of the end point on a cubic curve
     * @param y3 The y-coordinate of the end point on a cubic curve
     */
    public void cubicTo(float x1, float y1, float x2, float y2,
                        float x3, float y3) {
        isSimplePath = false;
        native_cubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
    }

其中起始点为此Path的上一个连接点,x1,y1为此曲线的第一个控制点,x2,y2为第二个控制点,x3,y3为结束点

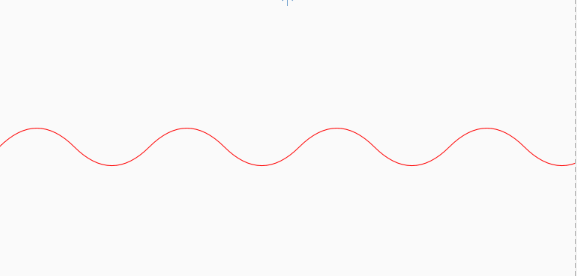
3 .实现案例一

Bizer4

案例分析:
1.我们可以将此效果看为是一个波形图
波峰波长
2.是由多个贝塞尔曲线链接的效果
案例实现:

1.新建一个自定义View，并且重写onDraw方法

public class TestBizerView extends View {

    public TestBizerView(Context context) {
        this(context,null);
    }

    public TestBizerView(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs,0);
    }

    public TestBizerView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
    }
}

2.重写onDraw方法并且初始化画笔设置

     /**
     * 初始化画笔
     */
    Paint mPaint;

    /**
     * 曲线起始点的坐标
     */
    private static int START_X_POINT=0;
    private static int START_Y_POINT=200;

    /**
     * 波长度
     */
    private static int WAVE_LENGTH=200;

    /**
     *波峰高度
     */
    private static int WAVE_HEIGHT=50;

    /**
     * 初始化画笔
     */
    public void init(){
        mPaint=new Paint();
        //1.设置画笔颜色
        mPaint.setColor(Color.RED);
        //2.设置抗锯齿
        mPaint.setAntiAlias(true);
        //3.设置画笔风格
        mPaint.setStyle(Paint.Style.STROKE);
    }
    
    @Override
    protected void onDraw(Canvas canvas) {
    }

3.简单的绘制一个波长(在onDraw中)

    @Override
    protected void onDraw(Canvas canvas) {
         //1.初始化一个Path路径
         Path p=new Path();
         //2.设置路径的起始点(Bizer的起始点)
          p.moveTo(START_X_POINT,START_Y_POINT);
         //3.绘制一个波长的贝塞尔曲线
         //控制点坐标:WAVE_LENGTH/4,START_Y_POINT-WAVE_HEIGHT    
         //结束点坐标:WAVE_LENGTH/2,START_Y_POINT
         p.quadTo(WAVE_LENGTH/4,START_Y_POINT-WAVE_HEIGHT,WAVE_LENGTH/2,START_Y_POINT);
         //以上一次的结束点为起始点
         p.quadTo(WAVE_LENGTH*3/4,START_Y_POINT+WAVE_HEIGHT,WAVE_LENGTH,START_Y_POINT);
         //4.绘制路径
         canvas.drawPath(p,mPaint);
   }

4.在布局中使用此自定义View

一个波长的Bizer

5.绘制多个波长

需要对OnDraw方法中的代码进行修改

@Override
    protected void onDraw(Canvas canvas) {
        //1.初始化一个Path路径
        Path p=new Path();
        //2.设置路径的起始点(Bizer的起始点)
        p.moveTo(START_X_POINT,START_Y_POINT);
        //3.绘制一个波长的贝塞尔曲线
//        //控制点坐标:WAVE_LENGTH/4,START_Y_POINT-WAVE_HEIGHT
//        //结束点坐标:WAVE_LENGTH/2,START_Y_POINT
//        p.quadTo(WAVE_LENGTH/4,START_Y_POINT-WAVE_HEIGHT,WAVE_LENGTH/2,START_Y_POINT);
//        //以上一次的结束点为起始点
//        p.quadTo(WAVE_LENGTH*3/4,START_Y_POINT+WAVE_HEIGHT,WAVE_LENGTH,START_Y_POINT);
        for (int i = 0; i <20 ; i++) {
                  p.quadTo(WAVE_LENGTH(i*2+1)/4,i%2==0?START_Y_POINTWAVE_HEIGHT:START_Y_POINT+WAVE_HEIGHT,WAVE_LENGTH(i+1)/2,START_Y_POINT);
        }
        //4.绘制路径
        canvas.drawPath(p,mPaint);
    }

Bizer4

代码链接:https://github.com/huangyiCode/TestBizerApp.git

4 .实现案例二

可以增加延时让水波可以动起来

实现案例二

代码链接:https://github.com/huangyiCode/TestBizerTwo

5 .实现案例三

拖拽功能

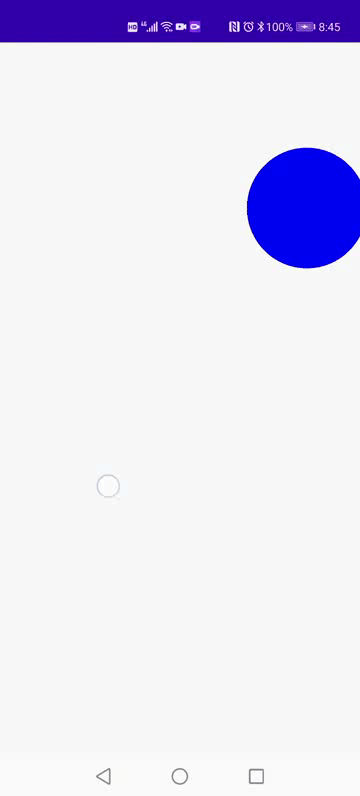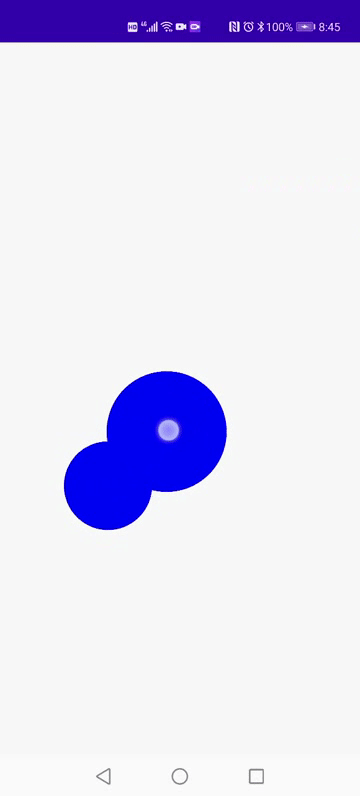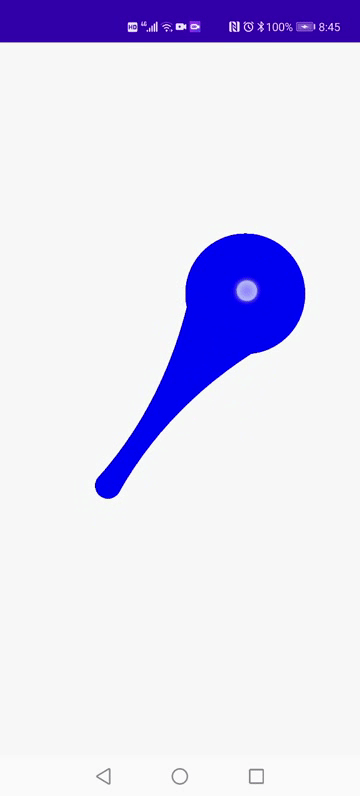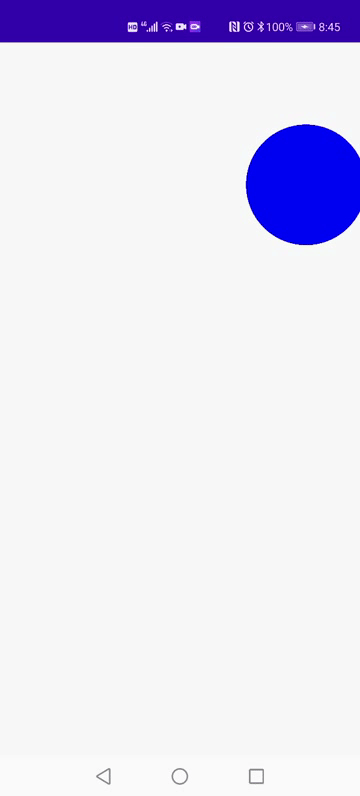
1.效果演示：

拖拽效果.gif

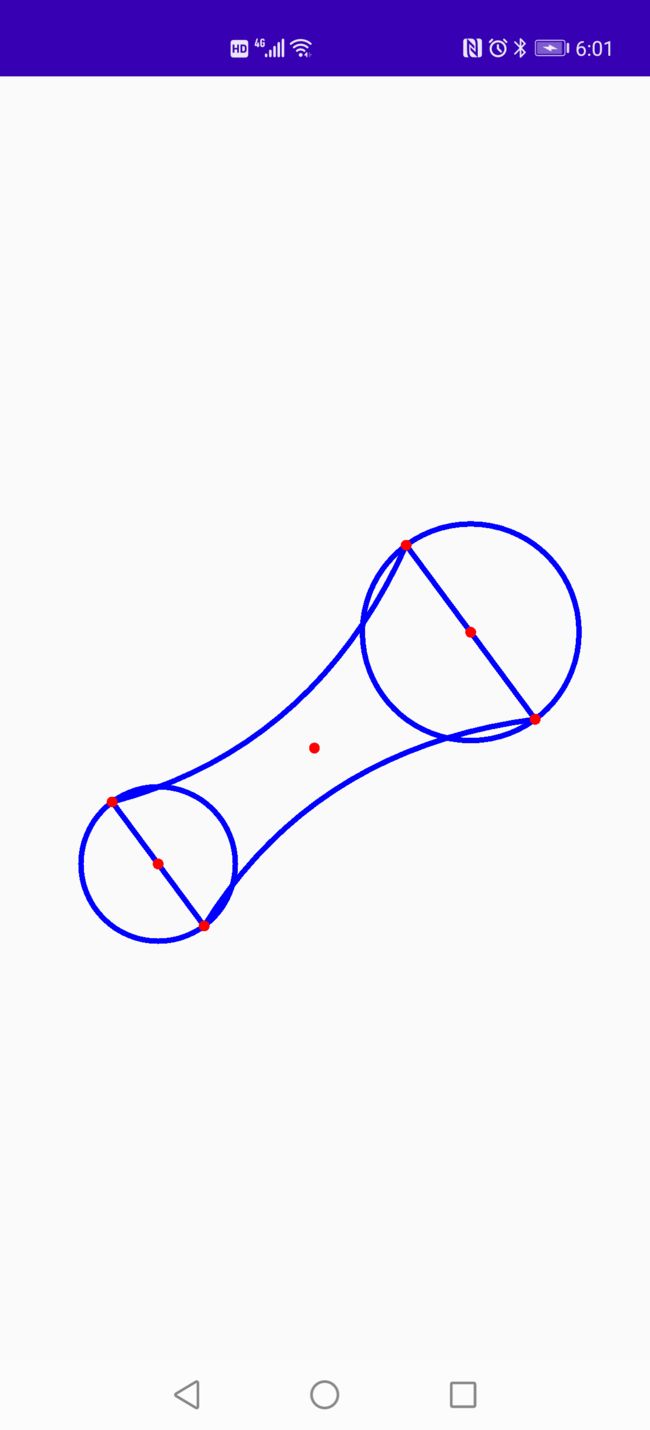
2.当我们看到有动画效果要实现上述的效果，首先需要把拖拽动画的其中一帧进行拆解，如果明白了一帧的绘制那么其他帧数时候的状态只是大同小异，例如下图：

独立的一帧拆解.png

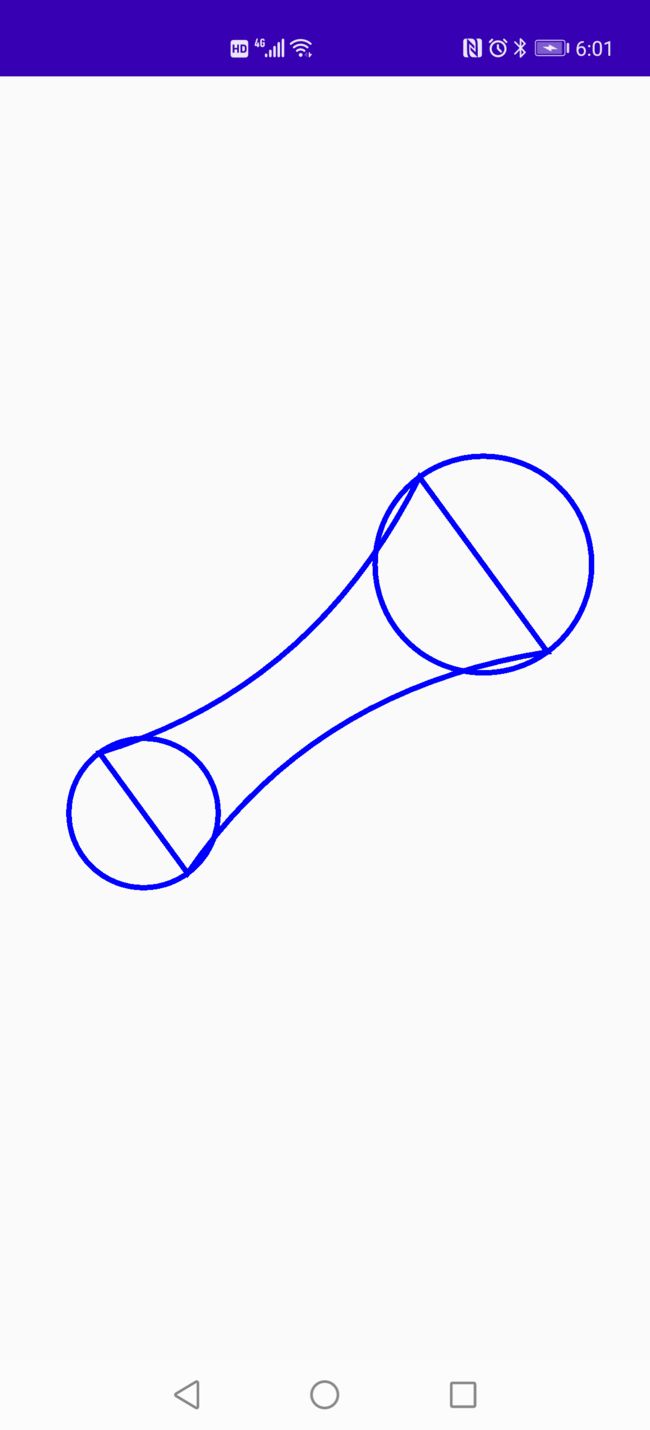
3.然后去掉填充效果,发现只是由两个圆，以及两条曲线组成，那么构成这张图片只需要下列元素

独立的一帧拆解(无填充).png

4.主要的定位元素:

1.两个圆的圆心以及半径用来绘制圆形
2.两条曲线的起始点以及控制点

如图所示我们可以发，圆形的位置会跟随手指的位置移动只是起始位置的圆大小会发生变化，以及拖拽部位圆的圆心会发生变化，这些用来定位绘制圆形的元素都比较容易获取，控制点如图我们可以分析出其实就是两条圆心的终点，那么难点就在如我们如何计算获取曲线起始点位置的坐标，如果我们可以根据圆的位置计算出动态起始点的坐标，那么久很容易实现上述演示的效果

主要端点.png

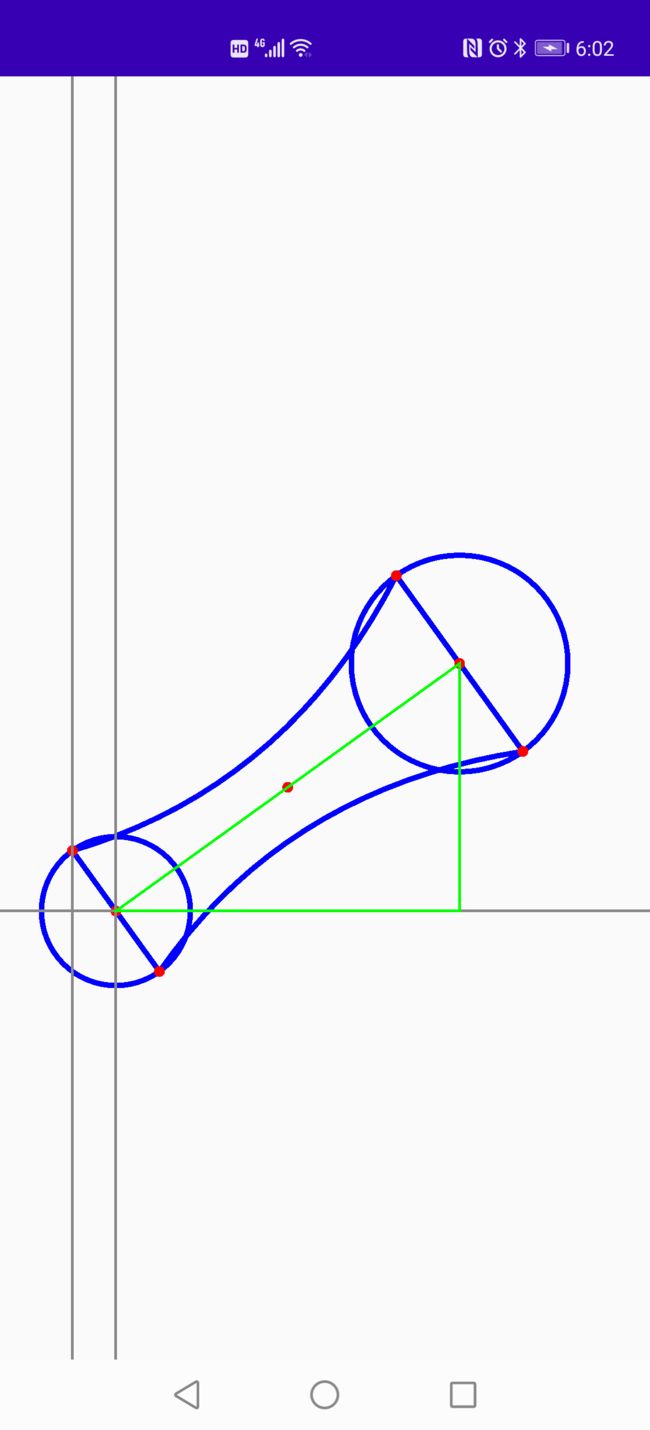
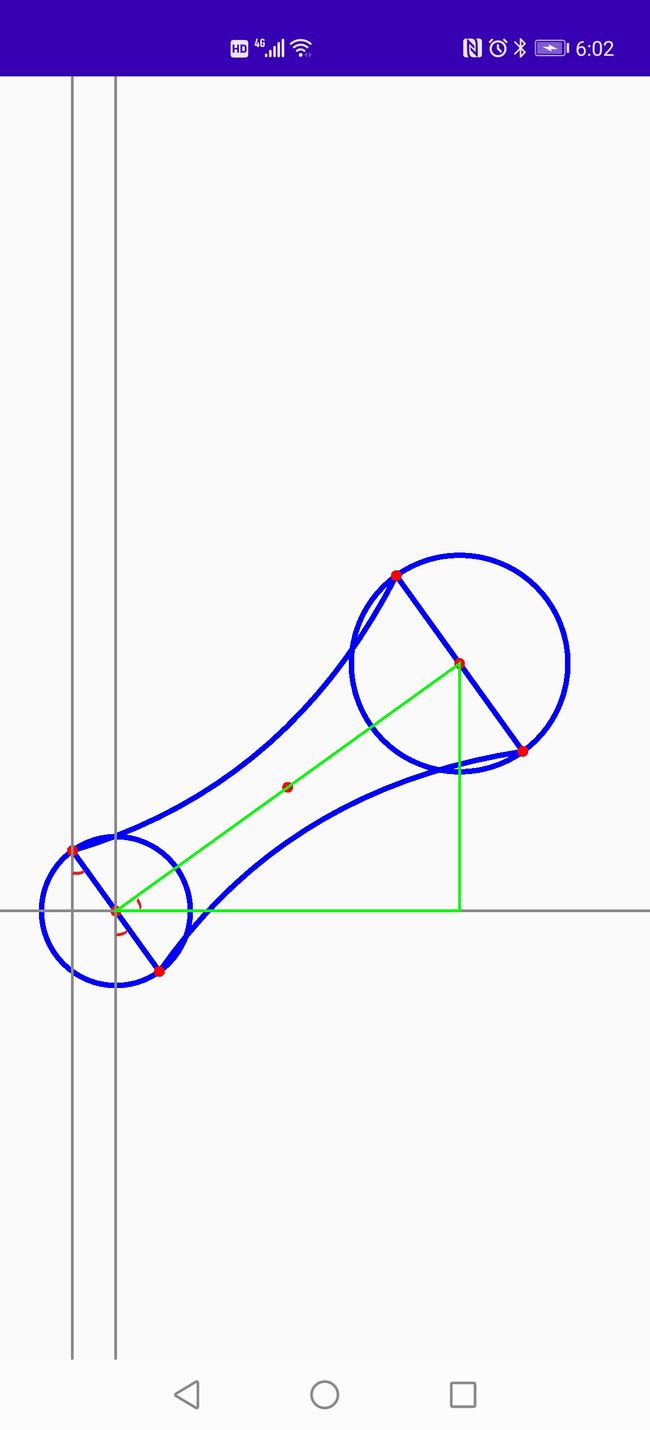
5.如何计算曲线起始点位置的坐标，我们来看下分析图，添加了一些辅助线，就像我们做几何题一样

偏移角度.png

如图所示，根据绿色部位，我们可以根据三角函数计算出拖拽圆相对于起始圆所偏移的角度，并且根据此角度我们可以计算出对应曲线起始点的坐标，我们可以看出下图三个位置的角度是相同的，如果我们计算出了绿色部位的角度那么就可以使用半径根据三角函数计算出曲线的对应端点位置的偏移量坐标，从而将其进行绘制，当我们掌握如何绘制一帧的数据之后，我们就很容易绘制动态的变化效果，只需要在监听View的触摸事件，当拖拽位置坐标发生变化之后重新绘制当前UI，从而达到动画效果

曲线端点计算.jpg

代码链接:
https://github.com/huangyiCode/TestBizerTwo/blob/master/app/src/main/java/com/example/hasee/testbizertwo/DragView.kt

6 .实现案例四

曲线.PNG

代码链接:
https://github.com/huangyiCode/TestBizerTwo/blob/master/app/src/main/java/com/example/hasee/testbizertwo/CircleView.kt

欢迎关注Mike的

Android 知识整理