这里使用蚁群算法求函数的最大值,函数是:
f = -(x.^4 + 3*y.^4 - 0.2*cos(3*pi*x) - 0.4*cos(4*pi*y) + 0.6);
步骤如下:
- 初始化参数。
- 初始化蚁群,第一代蚁群随机分布在可行域中。
- 初始化信息素,第一代信息素采用第一代蚁群的函数值表示,函数值越大,信息素越多。
- 状态转移,计算状态转移概率,根据状态转移概率进行局部搜索或全局搜索。
- 约束边界。
- 选择,根据目标函数值在原始蚁群和状态转移之后的蚁群之间进行选择。
- 更新信息素,tau = (1 - Rou) .* tau + calObjFun(ants)。
- 对选择后的蚁群重复进行状态转移、约束边界和更新信息素3步,直至结束。
主函数及结果
下面是主函数:
clear;
clc;
Ant = 300; % 蚂蚁数量
Times = 80; % 蚂蚁移动次数
Rho = 0.9; % 信息素挥发系数
P0 = 0.2; % 转移概率常数
xl = -1; xu = 1; % 设置搜索范围
yl = -1; yu = 1;
step = 0.05;
ants = initant(Ant, xl, xu, yl, yu); % 初始化蚁群
tau = calObjFun(ants); % 计算初代信息素
firstants = ants;
for t = 1:Times
ants = edgeselection(ants, P0, tau, 1/t, xl, xu, yl, yu); % 转移+约束
tau = (1 - Rho) .* tau + calObjFun(ants); % 更新信息素
end
figure(1);
plotobjfun(xl, xu, yl, yu, step);
hold on;
plot3(firstants(:,1), firstants(:,2), calObjFun(firstants), 'b*');
hold on;
plot3(ants(:,1), ants(:,2), calObjFun(ants), 'r*');
hold off;
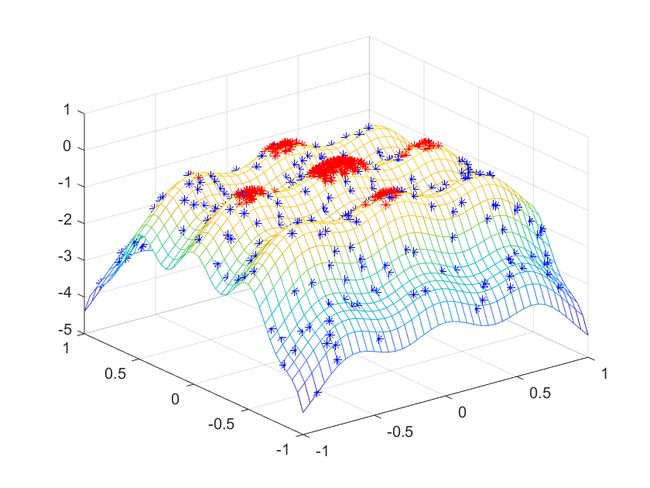
程序运行结果绘图如下,其中蓝色点为第一代蚁群,红色为最后一代蚁群:
状态转移和约束边界函数
函数说明如下:
function sants = edgeselection(ants, tau, P0, lamda, xl, xu, yl, yu)
% 状态转移 + 约束边界
% ants input 蚁群
% tau input 信息素
% P0 input 转移概率常数
% lamda input 局部搜索参数
% xl input x最小值
% xu input x最大值
% yl input y最小值
% yu input y最大值
% sants output 输出蚁群
下面计算函数的状态转移概率,进行局部搜索和全局搜索:
sants = ants;
% 计算状态转移概率
[taubest, ~] = max(tau);
p = abs((taubest - tau) / taubest);
lsindex = find(p < P0);
gsindex = find(p >= P0);
% 局部搜索
r = rand(length(lsindex), 2);
sants(lsindex, :) = sants(lsindex, :) + (2 .* r - 1) .* lamda;
% 全局搜索
r = rand(length(gsindex), 2);
gedge = repmat([xu-xl, yu-yl], length(gsindex), 1);
sants(gsindex,:) = sants(gsindex,:) + gedge .* (r - 0.5);
之后约束边界:
% 约束边界
sants(sants(:, 1) < xl, 1) = xl;
sants(sants(:, 1) > xu, 1) = xu;
sants(sants(:, 2) < yl, 2) = yl;
sants(sants(:, 2) > yu, 2) = yu;
最后进行选择:
% 选择
objvalue = calObjFun(ants);
sobjvalue = calObjFun(sants);
tindex = find(sobjvalue < objvalue);
sants(tindex, :) = ants(tindex, :);
一些其他函数
初始化蚁群函数:
function ants = initant(num, xl, xu, yl, yu)
% 初始化蚁群
% num input 蚂蚁数量
% xl input x最小
% xu input x最大
% yl input y最小
% yu input y最大
% ants output 蚁群
ants = rand(num, 2);
ants(:,1) = xl + (xu - xl) .* ants(:,1);
ants(:,2) = yl + (yu - yl) .* ants(:,2);
计算目标函数值函数:
function objval = calObjFun(X)
% 计算目标函数值
% X input 点输入 [x, y] nx2
% objvalue output 输出 nx1
objval = -(X(:,1) .^ 4 + 3 .* X(:,2) .^ 4 - 0.2 .* cos(3*pi .* X(:,1)) ...
- 0.4 .* cos(4*pi .* X(:,2)) + 0.6);
绘制函数图像函数:
function plotobjfun(xl, xu, yl, yu, step)
% 绘制函数图像
% xl input x最小值
% xu input x最大值
% yl input y最小值
% yu input y最大值
% step input 采样距离
[x, y] = meshgrid(xl:step:xu, yl:step:yu);
f = '-(x.^4 + 3*y.^4 - 0.2*cos(3*pi*x) - 0.4*cos(4*pi*y) + 0.6)';
z = eval(f);
mesh(x, y, z);