论文阅读 2013 — EDCircles: A real-time circle detector with a false detection control

这个文章是2013年圆检测的论文，发表在Pattern Recognition上，代码地址https://github.com/CihanTopal/ED_Lib，这个作者很有意思，除了一系列ED算法，检测直线，检测三角，检测圆等等。

我为什么要读这篇论文，这篇论文应用了LSD和ELSD，基于NFA的算法基本能够很好的去除虚假椭圆，而目前椭圆检测难点也确实在虚假椭圆的去除上，因此这个博客，仅分析方法和实验，介绍和相关结论就不说了。

1 摘要

作者提出了一个实时、无参数的圆检测算法，算法能够有效控制虚假圆的个数。该算法利用了无参数边缘检测算法EDPF产生的连续的边缘段集合，因此该算法被叫做EDCircles。该算法首先利用EDPF计算边缘段，之后转换为直线段。将检测到的直线段转换成圆弧，用两种启发式算法将圆弧连接起来，检测候选圆和近圆椭圆。基于Helmholtz原理，通过一个反向验证步骤对候选点进行验证，消除了只留下有效圆和近圆椭圆的错误检测。实验结果表明，EDCircles实时工作（640480幅图像10-20ms），检测率高，结果准确，非常适合于下一代实时视觉应用，包括成品自动检测、瞳孔检测、环形交通标志检测等。

2 EDCircles

算法流程

• 利用EDPF检测边缘段，提取完整的圆与椭圆。
• 将剩余边缘段转换为直线段。
• 通过组合直线段检测弧段。
• 组合弧段获取圆候选。
• 组合剩余弧度来检测近似椭圆候选。
• 使用Helmholtz原理验证候选圆与椭圆。
• 输出结果。

2.1 利用EDPF检测边缘段

Canny 通过识别图像中的一组潜在边缘像素，并通过非最大抑制、滞后阈值化、腐蚀等操作消除非边缘像素。

论文使用的边缘检测方法ED采用了一种主动的方法，首先确定图像中的一组点，称为锚点(anchors)，然后使用智能路由过程连接这些锚点；也就是说，ED实际上在图像中绘制边缘。ED不仅输出一个类似于传统边缘检测器输出的二值边缘图，而且还输出一组边缘段，每个边缘段是一个连续的（连接的）像素链。

ED有许多必须由用户设置的参数，这需要为不同类型的图像进行调参。EDPF利用了反向边缘验证机制，是一种无参数的边缘检测，能够去除虚假边缘，留下有意义的边缘。

下图是利用EDPF的检测结果，每个弧段用不同颜色表示出来。值得注意的是，场景中有很多封闭的圆合椭圆，因此在边缘提取之后，可以先验证封闭的轮廓。先利用圆你和算法对图形进行你和，如果你和误差小于1.5，那么将这个圆添加到候选中（误差小并不代表这个是实际的圆，还需要进一步的验证），如果圆拟合失败，再进行椭圆拟合，通过则扔进候选里。扔进候选里的弧段将不会参与后续的流程中。

之后，对于剩下的边缘段，作者使用EDLines算法对每个边缘段进行逼近，与EDLines不同，逼近后不会对弧段进行验证，产生的所有直线段将会在后续工作中处理。

2.2 圆弧段检测

算法约束每个圆弧段至少有3条直线段。分割过程与别的椭圆检测算法是相似的，若一对直线段之间的角度变化率过大或过小，都不会被认为是一个圆弧段，根据这个约束确定分割点，而且圆弧段的角度弯曲方向必须是一致的，这些都可以利用向量的内积外积来计算。根据实验，作者认为变化的角度在$[0^{\circ },60^{\circ }]$之间得到的圆弧段是最好的。

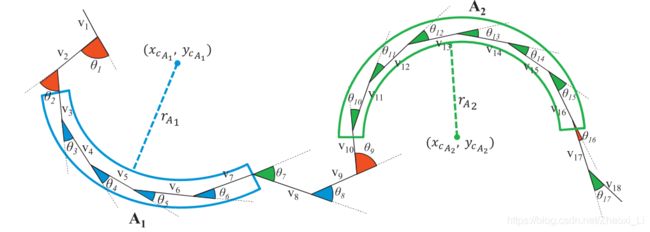
对提取出的一个弧段，直接进行圆你和，如果拟合误差<1.5pix，那么就将这个弧段添加到后选中。否则，先从3个弧段开始，一个一个的拟合，直到拟合误差超过1.5像素。

下图是最终的弧段提取结果，注意到有个虚假的椭圆候选，之后的验证会精准去除。

这个表格给出了每个弧段拟合之后的圆心、半径和弧段的启示结束角度（个人观点：小弧段拟合时候，对噪声异常敏感，根本不像这个表格给的这么近似，根据每个弧段的相似来组合是不靠谱的，改进时候也不要基于这个改进了，小弧段拟合误差敏感，不适用。）

2.3 组合弧段来检测候选圆和近圆椭圆

个人观点：不推荐这种组合方法，该论文是2013年的，建议多看看近几年的论文，组合算法本身就是椭圆检测的关键过程，近几年已经有了很多经典的算法。

首先根据弧段的长度来对弧段进行排序。之后先从最长的弧段开始扩展，扩展时候基于两个准则：

• 半径差异约束：两个弧段之间拟合出的半径差异在阈值内。比如弧段差异不能超过A1半径的25%
• 圆心距离约束。两个弧段的拟合圆心之间的距离在阈值内。比如圆心距离不能超过A1半径的25%。

下图是个示例，(a) 满足圆心约束，却不满足半径约束；(b)满足半径约束却不满足圆心约束。© 都满足，但是组合张量小于圆的一半。

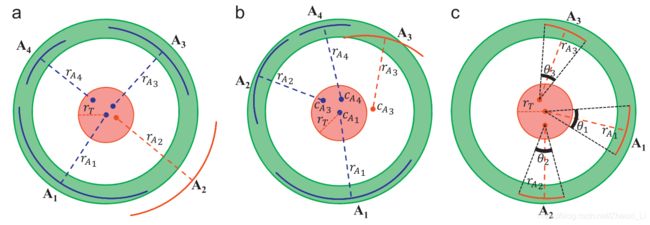
得到一个组合之后，进行拟合，如果参与拟合的弧段角度张量超过圆的一半，则作为一个圆候选，否则这些弧段留下来做近圆椭圆检测。

剩余的弧段用于进行近圆检测，思路与圆检测相似，都是用了圆心约束和半径约束，细节这里不说了（毕竟近几年已经有了更好的组合算法）。

2.4 利用Helmholtz准则验证圆和椭圆

先定义Helmholtz准则，为它的反向验证框架奠定基础，并描述它是如何在给定的图像中检测有意义的对齐段，也就是线段。

Helmholtz原理简单地说，对于一个具有感知意义的几何结构来说，在随机情况下，这种结构（分组或格式塔）偶然出现的期望必须非常低。这是一种相反contrario的方法，对象被检测为背景的异常值。如Desolneux等人所说的，一个合适的背景模型是所有像素都是独立的。最简单的这种模型是高斯白噪声。换句话说，在高斯白噪声图像中没有可感知的有意义的结构，]Desolneux等人使用Helmholtz原理在给定图像中找到有意义的对齐段alignments，即线段，不需要任何参数。他们的想法是计算给定图像的水平线方向场（与梯度方向场正交），并寻找具有相似水平线方向的连续像素集。

下图(a)展示了一张图的水平线方向场，组成线段的对齐像素标记在矩形内，作者定义了对齐的含义如下：两个点（或直线段）$P,Q$在精度$p=1/n$下有相同的方向，即对其，如果$angle(P),angle(Q)$彼此相差$p\pi =\pi /n$度。Desolneux等人指出，与心理学和数值实验一直，$n$的实际值在32到4之间，考虑更大的n是没用的。在EDCircles中，选择$n=8$，也就是认为方向差异在$22.5^{\circ }$以内是对其的。

用Helmholtz原理进行验证，Desolneux等人定义了直线段的NFA(number of false alarms)：在一个尺寸为$N\times N$的图像下，直线段$L$长度为$n$，且至少有$k$个点与直线段方向对齐。定义$L$的NFA如下：

$$NFA(n,k)=N^4\sum _{i=k}^n{C}_n^k{p}^i(1-p{)}^{n-i}$$

其中$N^4$表示潜在的直线段个数(我觉得这里有点扯，实际上潜在直线段个数应该是$C_{N^2}^2$，如果说数量级是4次，倒是能理解)。这里的$p=1/8$就是前面表示的对其值。如果$NFA(n,k)\le ϵ$，则接受这个直线段，否则拒绝。作者给的建议是$ϵ=1$

（个人理解：作者认为直线段是否有效与图像尺寸相关，的确，越大的图像小的直线越被认定为噪声，但是对于ROI图像，或遥感图像，感觉这种常识就没意义，所以NFA这个思路确实很好，但是应该有些改进，应该只考虑局部直线段是不是即可）

将该思想应用在圆检测上，其思想非常简单：就像一组相邻的像素（其水平线角度与线段对齐）构成线段一样，一组相邻的像素（其水平线角度与圆对齐）构成圆。上图(b)示出了图像的水平线方向场，其中构成圆的对齐像素被标记在两个圆内。为了定义像素和圆之间的对齐方法，给出了如下定义：如果在圆的边界上的像素点$P$与对应的圆的切向方向对齐，则称$P$与圆对齐。上图（c）显示了圆边界上几个点的梯度方向（垂直于水平线角度），其中一些点与圆对齐，而一些点与圆不对齐。灰色三角形表示理想梯度方向和观测梯度方向之间的差异，如果观测梯度方向在圆锥内部，则假定该点与圆对齐，否则假定该点与圆不对齐。为了区别圆和椭圆，对于椭圆使用$NFA(n,k)=N^5{\sum }_{i=k}^n{C}_n^k{p}^i(1-p{)}^{n-i}$

3 实验结果

下图是几个实验结果：

13年时候，算法量化没有这么标准，基本都是疯狂放图，整体上看，EDCircles确实有了质的提升。

4 总结

根据这篇论文，我个人提出几个自己的看法。

• 1 边缘检测可以参考论文提出的EDPF的方法，但是多边形逼近，最好用2012年Prasad提出的自适应逼近。
• 2 弧段分割思想很通用，没什么特殊的。
• 3 组合思想，不建议使用了，近几年已经有了更好的，这个组合方法有很大限制的。
• 4 验证思想，非常好，我目前也在研究这个点，感觉基于仿生和心理学的视觉验证才是方向。