2020蓝桥杯 C++ B组 国赛(python实现)
题目链接:https://blog.csdn.net/qq_46144509/article/details/109699279?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-1&spm=1001.2101.3001.4242
D 本质上升序列
【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
思路:
这道题一看就需要使用动态规划,题目给出了两个条件,必须满足字符串是单调递增的,比如la就不是lanqiao的递增子序列,然后必须是本质不同的子序列,于是可以用dp[i]代表第i个字符结尾的递增子序列个数,动规方程就是
dp[i] += dp[j] jvalue[j]
dp[i] -= dp[j] j第一个方程比较好理解,主要是第二个方程,可以理解成在本质相同的子序列中,只考虑最开始出现的那一个,比如遍历到i个位置发现第j个位置和它的数值相同,表示重复dp[j]个数列了,于是减去
代码
s=list(input())
n=len(s)
cnt=[1]*n
for i in range(n):
for j in range(i):
if s[i] > s[j]:
cnt[i] += cnt[j]
if s[i] == s[j]:
cnt[i] -= cnt[j]
print(sum(cnt))
E 玩具蛇
【问题描述】
小蓝有一条玩具蛇,一共有 16 节,上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
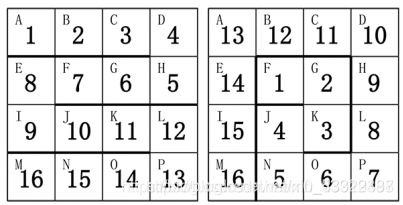
请帮小蓝计算一下,总共有多少种不同的方案。如果两个方案中,存在玩具蛇的某一节放在了盒子的不同格子里,则认为是不同的方案。
思路:
这道题也就是从任何一个位置开始放,纪录走过的路径,进行dfs搜索,如果该种方式最后走完了所有节点就使ans+
H 答疑
【问题描述】
有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。
老师可以安排答疑的顺序,同学们要依次进入老师办公室答疑。
一位同学答疑的过程如下:
首先进入办公室,编号为 i 的同学需要 si 毫秒的时间。
然后同学问问题老师解答,编号为 i 的同学需要 ai 毫秒的时间。
答疑完成后,同学很高兴,会在课程群里面发一条消息,需要的时间可以忽略。
最后同学收拾东西离开办公室,需要 ei 毫秒的时间。一般需要 10 秒、
20 秒或 30 秒,即 ei 取值为 10000,20000 或 30000。
一位同学离开办公室后,紧接着下一位同学就可以进入办公室了。
答疑从 0 时刻开始。老师想合理的安排答疑的顺序,使得同学们在课程群
里面发消息的时刻之和最小
【输入格式】
输入第一行包含一个整数 n,表示同学的数量。
接下来 n 行,描述每位同学的时间。其中第 i 行包含三个整数 si, ai, ei,意
义如上所述。
【输出格式】
输出一个整数,表示同学们在课程群里面发消息的时刻之和最小是多少。
【样例输入】
3
10000 10000 10000
20000 50000 20000
30000 20000 30000
【样例输出】
280000
【样例说明】
按照 1, 3, 2 的顺序答疑,发消息的时间分别是 20000, 80000, 180000。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ n ≤ 20。
对于 60% 的评测用例,1 ≤ n ≤ 200。
对于所有评测用例,1 ≤ n ≤ 1000,1 ≤ si ≤ 60000,1 ≤ ai ≤ 1000000, ei ∈ {10000, 20000, 30000},即 ei 一定是 10000、20000、30000 之一。
思路
https://blog.csdn.net/ylwhxht/article/details/109694494
引用上面博主的图,因为计算sum之后加上ci的累加就跟(ai+bi+ci)有关系了,所以要保证最前面的(ai+bi+ci)最小,
程序
n = int(input())
f = []
for _ in range(n):
a,b,c = map(int, input().split())
f.append((a+b,c)) #使用append
f.sort(key = lambda x : (x[0]+x[1]))
res,time = f[0][0],f[0][0] #记录答案和当前发送消息的时间
for i in range(n-1):
time += (f[i][1]+f[i+1][0])
res += time
print(res)
游园安排
这道题就是一道递增子序列的题目,难度不高,也是因为力扣上面真的有很多递增子序列的题目,解题总共分为以下几个步骤:
1.提取出名字构建一个列表
2.进行动态规划
3.在最长的序列中找到字符串大小最小的序列
代码: (比较冗余,但是思路还是挺易懂的)
s = input()
start,end = 0,0
string = []
str = ''
#成功分解出来了
while(end<len(s)):
str+=s[end]
end+=1
if(end ==len(s) or 'A'<=s[end]<='Z' ):
string.append(str)
str=''
dp = [[1,j] for i,j in enumerate(string)] #
for i in range(len(string)):
for j in range(i):
if(string[i]>string[j]): #必须要单调递增
if(dp[j][0]+1>dp[i][0]):
dp[i][0] = dp[j][0]+1
dp[i][1] = dp[j][1]+string[i]
elif(dp[j][0]+1==dp[i][0] and dp[i][1]>dp[j][1]+string[i]): #如果相同比较字符串的相对大小
dp[i][1] = dp[j][1]+string[i]
maxvalue=float('-inf')
for i in range(len(string)): #找到最大的长度
maxvalue = max(maxvalue,dp[i][0])
ans = 'z'*maxvalue
for i in range(len(string)):
if(dp[i][0] == maxvalue and ans>dp[i][1]): #依次找到相同长度下排序最小的序列
ans = dp[i][1] #这
print(ans)
H: 画廊
题目:
【问题描述】
小蓝办了一个画展,在一个画廊左右两边陈列了他自己的作品。为了使画 展更有意思,小蓝没有等距陈列自己的作品,而是按照更有艺术感的方式陈列。 在画廊的左边陈列了 L 幅作品,在画廊的右边陈列了 R 幅作品,左边的作品距 离画廊的起点依次为 u1, u2, · · · , uL,右边的作品距离画廊起点依次为 v1, v2, · · · , vR。 每周,小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的, 但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。 小蓝从画廊的起点的正中央(左右两边的中点)出发,整理好每一幅画, 最终到达画廊的终点的正中央。已知画廊的宽为 w。 请问小蓝最少带着工具走多长的距离?
【输入格式】
输入的第一行包含四个整数 L, R, d, w,表示画廊左边和右边的作品数量,
以及画廊的长度和宽度。
第二行包含 L 个正整数 u1, u2, · · · , uL,表示画廊左边的作品的位置。
第三行包含 R 个正整数 v1, v2, · · · , vR,表示画廊右边的作品的位置。
【输出格式】
输出一个实数,四舍五入保留两位小数,表示小蓝最少带着工具走的距离。
【样例输入】
3 3 10 2
1 3 8
2 4 6
【样例输出】
14.71
【样例说明】
小蓝从起点开始,首先到达左边第一幅作品(走动距离 √2),然后到达左
边第二幅作品(走动距离 2),然后到达右边第一幅作品(走动距离 √5),然后
到达右边第二幅和第三幅作品(走动距离 2 和 2),然后到达左边第三幅作品
(走动距离 2 √2),最后到达画廊终点(走动距离 √5)。
总共距离为 √
2 + 2 + √
5 + 2 + 2 + 2 √
2 + √5 ≈ 14.71。
【评测用例规模与约定】
对于 40% 的评测用例,1 ≤ L, R ≤ 10, 1 ≤ d ≤ 100, 1 ≤ w ≤ 100。
对于 70% 的评测用例,1 ≤ L, R ≤ 100, 1 ≤ d ≤ 1000, 1 ≤ w ≤ 1000。
对于所有评测用例,1 ≤ L, R ≤ 500, 1 ≤ d ≤ 100000, 1 ≤ w ≤ 100000, 0 ≤ u1 < u2 < · · · < uL ≤ d, 0 ≤ v1 < v2 < · · · < vR ≤ d。
这道题就是一道定了起点和原点的TSP问题,我写的像个最小生成树,写的贪心算法,但是查了查好像都没有可以解决起点和源点都定了的TSP问题,需要注意的是需要最后到达的必须是终点,自己写的实在是太辣鸡了。希望巨巨们提供下别的思路
import heapq
import math
from collections import defaultdict
L,R,d,w = map(int,input().split()) #输入数据
loc = []
seen = [0 for i in range(L+R+2)] #使用
weight = []
def calculate(x,y):
return math.sqrt((x[0]-y[0])**2 + (x[1]-y[1])**2)
maxvalue = float('-inf')
u = list(map(int,input().split()))
print(u)
for i in u:
loc.append((i,0))
v = list(map(int,input().split()))
for i in v:
loc.append((i,w))
loc.append((0,w/2)) #第一个点
loc.append((d,w/2)) #最后一个点
print(loc)
for i in range(L+R+2):
for j in range(i):
temp = calculate(loc[i],loc[j]) #一直计算两者之间的距离
heapq.heappush(weight,(temp,i,j)) #计算
sumvalue=0
seen[L+R]=1 #
print(weight)
m=0
while(m<L+R+1):
minvalue = float('inf')
for value,x,y in weight:
if(seen[x] +seen[y]==1 and minvalue>=value):
if((x==L+R+1 or y==L+R+1) and m!=L+R): #如果
continue
tempx,tempy = x,y
minvalue = value
sumvalue+=minvalue
print(tempx,tempy,minvalue)
seen[tempx]+=1
seen[tempy]+=1 #使其只能走过一次
m+=1
print(seen)
print(sumvalue)
试题I:补给
解析:待更…
试题J:质数行者
解析:待更…






