力扣算法篇：二分查找

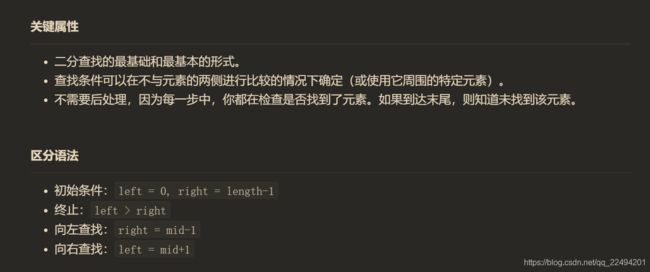
二分查找1.0

自己实现一个二分查找：

class Solution {
     
public:
    int search(vector<int>& nums, int target) {
     
        //二分查找
        int left = 0;
        int right = nums.size()-1;
        while(left<=right){
     
            //为防止数据太大溢出 可使用 mid = 左+（右-左）/2
            int mid = (left+right)/2;
            if(nums[mid]==target){
     
                return mid;
            }
            //定左侧还是右侧
            if(target<nums[mid]){
     
                //更改右侧值
                right = mid-1;
            }else{
     
                //更改左侧值
                left = mid+1;
            }
        }
        //出来了 没找到
        return -1;
    }
};

模板

模板一：寻找一个数

int binarySearch(vector<int>& nums, int target){
     
  if(nums.size() == 0)
    return -1;
  int left = 0, right = nums.size() - 1;
  while(left <= right){
     
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){
      return mid; }
    else if(nums[mid] < target) {
      left = mid + 1; }
    else {
      right = mid - 1; }
  }
  return -1;
}

关键点：

练习-x的平方根

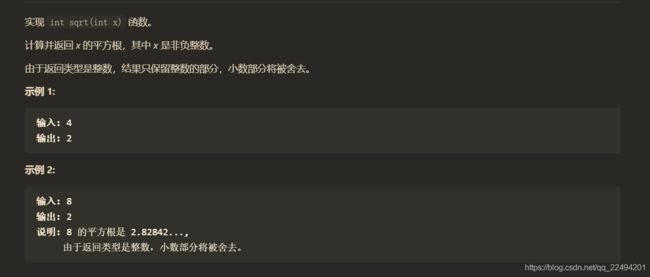
题解：注意溢出 找不到时 最后判断结果是mid还是mid-1

class Solution {
     
public:
    int mySqrt(int x) {
     
        //考虑x为0的情况
        if(x == 0){
     
            return 0;
        }
        //求某数的平方根 不为整数时舍去小数 采用二分查找 从1-n
        int left = 1;
        int right = x;
        int mid = 0;
        while(left<=right){
     
            //计算mid
            mid = left+(right-left)/2;
            long mid_2 = (long)mid*mid;
            if(mid_2 == x){
     
                return mid;
            }
            //定左侧还是右侧
            if(mid_2<x){
     
                left = mid+1;
            }else{
     
                right = mid-1;
            }
        }
        return (long)mid*mid<=x ? mid:mid-1;
    }
};

练习-猜数字大小

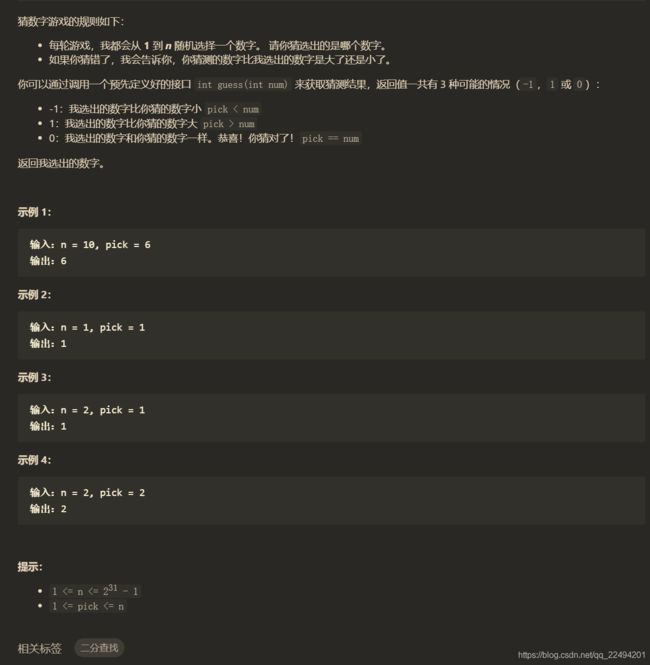
题解：防溢出 mid = left+（right-left）/2;

/** 
 * Forward declaration of guess API.
 * @param  num   your guess
 * @return 	     -1 if num is lower than the guess number
 *			      1 if num is higher than the guess number
 *               otherwise return 0
 * int guess(int num);
 */
class Solution {
     
public:
    int guessNumber(int n) {
     
       //二分查找
       int left = 1;
       int right = n;
       while(left<=right){
     
           int mid = left+(right-left)/2;
           int temp = guess(mid);
           if( temp == 0){
     
               //猜对了
               return mid;
           }
           //没猜对
           if(temp == -1){
     
               //pick
               right = mid-1;
           }else{
     
               //pick>mid
               left = mid+1;
           }
       }
       //总能找到滴
        return 0;
    }
};

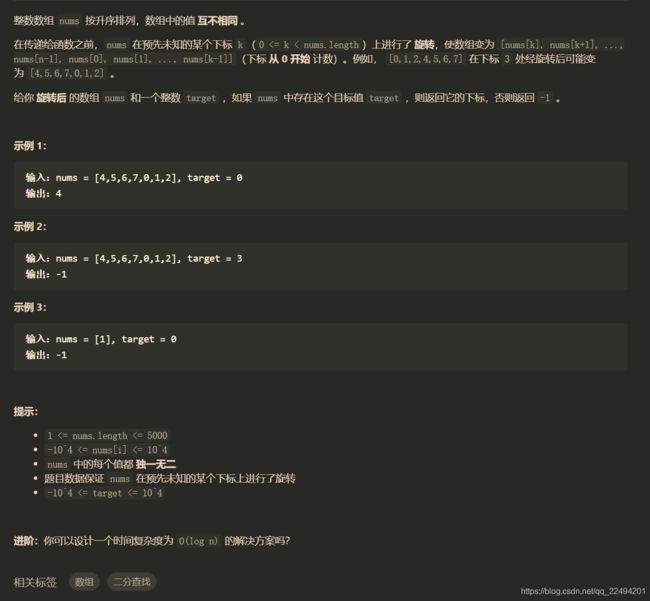
练习-搜索旋转排序数组

题解：

class Solution {
     
public:
    int binarysearch2(vector<int>& nums, int left,int right, int target) {
     
        //二分查找
        while(left<=right){
     
            //为防止数据太大溢出 可使用 mid = 左+（右-左）/2
            int mid = (left+right)/2;
            if(nums[mid]==target){
     
                return mid;
            }
            //定左侧还是右侧
            if(target<nums[mid]){
     
                //更改右侧值
                right = mid-1;
            }else{
     
                //更改左侧值
                left = mid+1;
            }
        }
        //出来了 没找到
        return -1;
    }
    int search(vector<int>& nums, int target) {
     
        //在不排序的情况下使用二分查找找出目标值
        //该数组原来有序 则旋转后 两区间部分有序（升序） 找出断点 断点 前>后 或者是以0为旋转点 本身有序
        int trancenter = 0; 
        for(int i = 1;i<=nums.size()-1;i++){
     
            if(nums[i]<nums[i-1]){
     
                //断点为i
                trancenter = i-1;
                break;
            }
        }
        //在断点的左右两侧使用二分查找
        int result = binarysearch2(nums,0,trancenter,target);
        if(result != -1){
     
            return result;
        }
        result = binarysearch2(nums,trancenter+1,nums.size()-1,target);
        if(result != -1){
     
            return result;
        }
        return -1;
    }
};

进阶：

class Solution {
     
public:
    int search(vector<int>& nums, int target) {
     
        //在不排序的情况下使用二分查找找出目标值
        //该数组原来有序 则旋转后 两区间部分有序（升序） 
        int left = 0;
        int right = nums.size()-1;
        while(left<=right){
     
            int mid = (left+right)/2;
            if(nums[mid] == target){
     
                return mid;
            }
            //left到mid是升序
            if(nums[left]<=nums[mid]){
     
                //看target在哪 left和mid之间
                if(nums[left]<=target && target<nums[mid]){
     
                    right = mid-1;
                }else{
     //mid和right之间
                    left = mid+1;
                }
            }else{
     
                //升序段在mid左边  nums[left]>nums[mid]
                //mid右边是升序段 mid到right 看target在哪 
                //mid和right之间
                if(nums[mid]<target&&target<=nums[right]){
     
                    left = mid+1;
                }else{
     //left和mid之间
                    right = mid-1;
                }
            }
        }
        return -1;
    }
};

模板二 寻找左侧边界

int binarySearch(vector<int>& nums, int target){
     
  if(nums.size() == 0)
    return -1;

  int left = 0, right = nums.size();
  while(left < right){
     
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){
      return mid; }
    else if(nums[mid] < target) {
      left = mid + 1; }
    else {
      right = mid; }
  }

  // Post-processing:
  // End Condition: left == right
  if(left != nums.size() && nums[left] == target) return left;
  return -1;
}

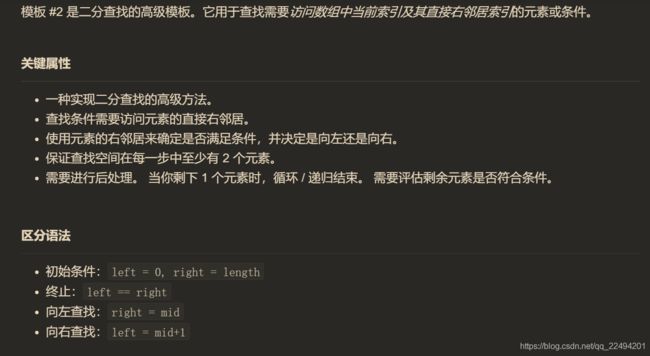
注意到初始条件是left=0,right=n,即左闭右开区间。

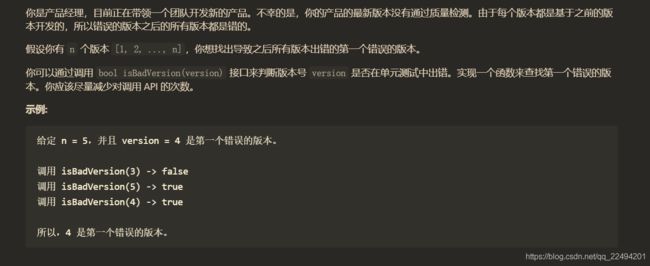
练习题-第一个错误的版本

题解：

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
     
public:
    int firstBadVersion(int n) {
     
        //寻找第一个错误的版本 二分法
        int left = 0;
        int right = n;
        while(left<right){
     
            //计算中间值
            int mid = left+(right-left)/2;
            //判断该产品是否为错误版本
            if(isBadVersion(mid)){
     
                //该版本为错误版本 right定位到mid
                right = mid;
            }else{
     
                //不是错误版本 left定位到mid+1
                left = mid+1;
            }
        }
        //出来的条件是left =right left 意为最左边的错误版本 即第一个错误版本
        return left;
    }
};