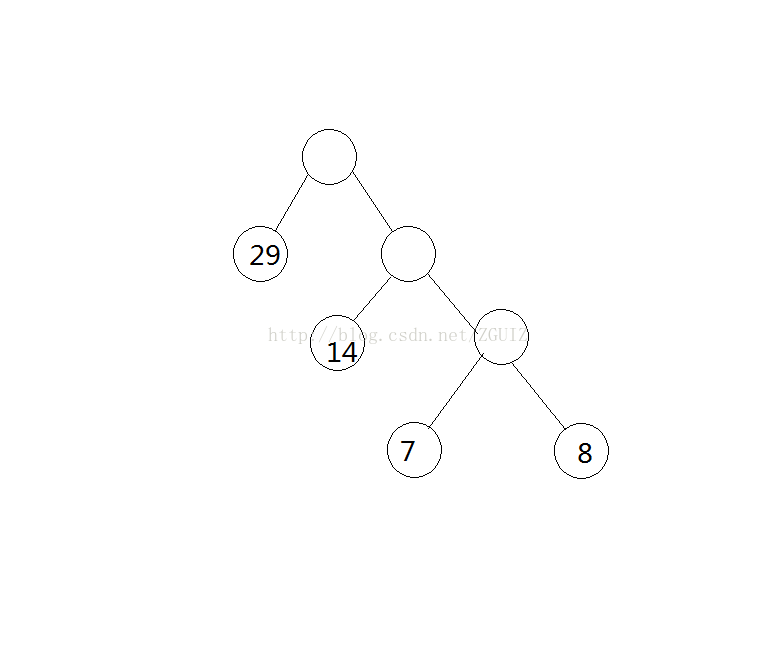
C语言哈夫曼树和哈夫曼编码的实现
哈夫曼树是一类带权路径(WPL)最短的的树。下面说一下实现代码:
首先仍然是类型定义:
typedef char **HuffmanCode;
typedef struct{
int weight;
int parent, lchild, rchild;
}HTNode,*HuffmanTree;
选择函数:
void Select(HuffmanTree HT, int i,int *s1,int *s2)
{
int j;
*s1 = 0;
*s2 = 0;
for (j = 1; j <= i; j++)
{
if (HT[j].parent == 0 && HT[*s1].weight > HT[j].weight)
{
*s2 = *s1;
*s1 = j;
}
else
if (HT[j].parent == 0 && HT[*s2].weight > HT[j].weight)
*s2 = j;
}
}
先让s1和s2指向0号位置(在下面创建函数中会把s1和s2号位置的权值设置为最大值),在已经储存权值的位置检查是否存在双亲为0并且权值比s1小的节点,如果有,则将s1的储存的位置赋值给s2(由于s1必然小于或等于s2,所以当发现有权值比s1小的节点时,s1中储存的节点变为权值第二小的节点,而s2正好用来储存第二小节点的地址),之后让j的值赋值给*s1。如果不存在权值比s1小的节点,则判断它的权值是否比s2的小(其权值有可能介于s1指向节点的权值和s2指向节点权值之间)。如果小于s2指向的权值,则将j赋值给*s2。
创建哈夫曼树:
HTNode *CreateHuffmanTree(HuffmanTree HT, int n)
{
int m, i, s1, s2;
if (n <= 1)
return HT;
m = 2 * n - 1;
HT = (HTNode *)malloc(sizeof(HTNode)*(m + 1));
for (i = 0; i <= m; i++)
{
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
}
HT[0].weight = 9999;
for (i = 1; i <= n; i++)
scanf("%d", HT[i].weight);
for (i = n + 1; i <= m; i++)
{
Select(HT, i - 1, &s1, &s2);
HT[i].lchild = s1;
HT[i].rchild = s2;
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
return HT;
}
先判断这棵树是否只有一个节点,如果仅仅只有一个,则不需要创建哈夫曼树,返回。确定m的值,哈夫曼数所有节点的数目。为哈夫曼树分配(m+1)个节点空间,并将所有节点的双亲、左右孩子均赋值为0,表示没有双亲、左右孩子。将0号节点的权值赋值为一个很大的值,并输入n个节点的权值。最后,从n+1号结点开始作为双亲结点,依次找到最小两个节点的位置,并将其双亲设置为i,将i号节点的左右子树分别设置为s1、s2,权值为左右子树权值之和。直到i<=m为止。
构造哈夫曼编码:
HuffmanCode CreateHuffmanCode(HuffmanTree HT, HuffmanCode HC, int n)
{
int i, start, f, c;
char *cd;
HC = (char **)malloc(sizeof(char *)*(n + 1));
cd = (char *)malloc(sizeof(char)*n);
cd[n - 1] = '\0';
for (i = 1; i <= n; i++)
{
start = n - 1;
c = i;
f = HT[i].parent;
while (f != 0)
{
--start;
if (c == HT[f].lchild)
cd[start] = '0';
else
cd[start] = '1';
c = f;
f = HT[f].parent;
}
HC[i] = (char *)malloc(sizeof(char)*(n - start));
strcpy(HC[i], &cd[start]);
}
delete cd;
return HC;
}
为HC分配n+1个char *空间,为cd分配n个空间,并将’\0’赋值给cd最后一位。依次获得哈夫曼编码:每一次都将start定位到n-1处,即cd的最后一位,然后让c等于要获得编码的位置(即i),f等于c的双亲,当c的双亲不为0的时候重复执行将start向前移动一位,判断c是不是f号节点的左子树,如果是,则cd[start]则为’0‘(char类型),否则为’1’,c移动到原来c的双亲上,f移动到原来f的双亲上。为HC[i]分配适当空间(n-start个),将cd的内容复制到HC[i]中。获得所有哈夫曼编码后,释放cd分配的空间。
加入main():
int main(void)
{
HuffmanCode HC;
HuffmanTree HT;
int n, i;
HT = NULL;
HC = NULL;
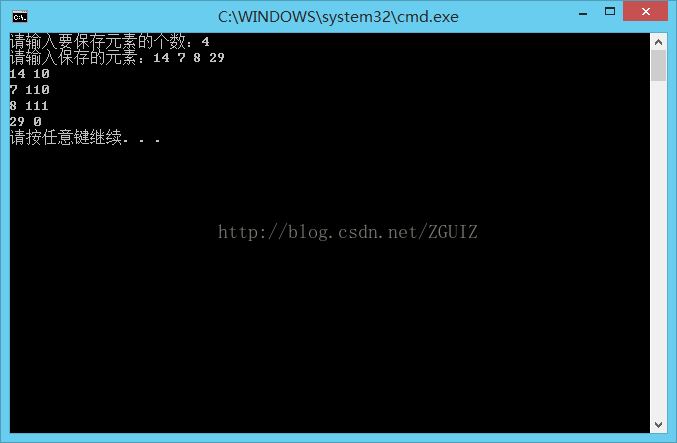
printf("请输入要保存元素的个数:");
scanf("%d", &n);
fflush(stdin);
printf("请输入保存的元素:");
HT = CreateHuffmanTree(HT, n);
HC = CreateHuffmanCode(HT, HC, n);
for (i = 1; i <= n; i++)
{
printf("%d %s\n", HT[i].weight, HC[i]);
}
return 0;
}