浅谈哈夫曼编码(含matlab代码)

浅谈哈夫曼编码

美国计算机科学家大卫·霍夫曼（David Albert Huffman）在1952年“种了”一棵树——哈夫曼树。

哈夫曼树

哈夫曼树的构造

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。

摘自维基百科——霍夫曼编码

哈夫曼树WPL值的计算

树的路径长度是从树根到每一结点的路径长度之和，记为WPL。
$$WPL=（W1\ast L1+W2\ast L2+W3\ast L3+...+Wn\ast Ln）$$
N个权值Wi（i=1,2,…n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,…n）。

• 举一栗子
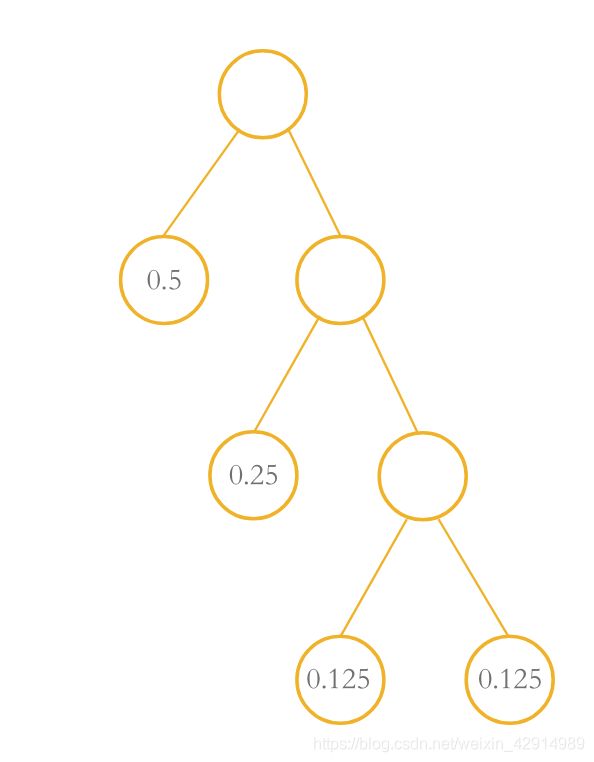
  有这么一颗哈夫曼树：

圆圈里面的数值为权值，连接的树干为路径，可计算其WPL：
$$WPL=（0.5\ast 1+0.25\ast 2+0.125\ast 3+0.125\ast 3）=1.75$$

一个叶子结点出现频率越高,就让他分布在离根结点越近的地方,也就是根结点走到该节点经过的路径长度越短，这样所构成的树称为哈夫曼树，所得WLP也最小。

哈夫曼编码

引入哈夫曼编码

有一组字符信息 “cbadd”，共有5个字符。

用普通等长码的表示方法时，每个英文字母均占用一个字节，即8个比特。
故共需要5*8 = 40位，显然这是一种较浪费内存的储存编码方式。

有小伙伴提出，假若我们给他编上不等码，那岂不是能减少所占用的内存了嘛。
这个idea不错，那么我们应该要怎么编码呢。

试试随意编码，令a：00 ，b：01 ,c：0 ,d：1

字符	随意编码
a	00
b	01
c	0
d	1

“cbacd” 的编码为 “0010001”
肉眼可见通过随意编码“cbadd”占用的内存为7位，这样子明显能减少编码所占用的内存。小伙伴们开始觉得，嗯，这个方法不错，以后就这样编码好嘞。

可是细心的同学就会注意到，通过随意编码是能减少储存信息所占用的内存，可是在解码的过程中“0010001”可译为“ccdcccd”、’“cbcad”、“adacd”等多种结果，可见随意编码可能造成信息解码二义性甚至多义性的结果，所以这个方法需要改进。

既想编码占用内存小，解码结果又唯一表示原信息，哈夫曼在哈夫曼树下冥思苦想，抬头的霎那间看见哈夫曼树那奇怪而有规律的二叉分枝，顿时有了灵感，想到了一种全新的编码方式，后来人们称之为哈夫曼编码。

哈夫曼编码的原理

设有一信源产生四种字符a、b、c、d，他们出现的概率分别为0.125，0.125，0.5，0.25。首先我们按照他们出现的概率从小到大依次排列，将最小的两个概率提取出来作为左右孩子节点（一般默认左孩子所在路径为“0”，右孩子所在路径为“1”）相加得到根结点。
此后将跟节点数值加入到队列中重新排队，同样步骤将最小的两个概率提取出来作为孩子节点相加得到根结点，依次操作，直至队列中的概率元素全部清空。最后得到哈夫曼树，生成四种字符的哈夫曼编码。

字符	a	b	c	d
概率数值	0.125	0.125	0.5	0.25
第一次排序	1	2	4	3
概率数值		0.25	0.5	0.25
第二次排序		1	3	2
概率数值			0.5	0.5
第三次排序			1	2

为轻松了解哈夫曼树形成的整一个过程，我们来看图

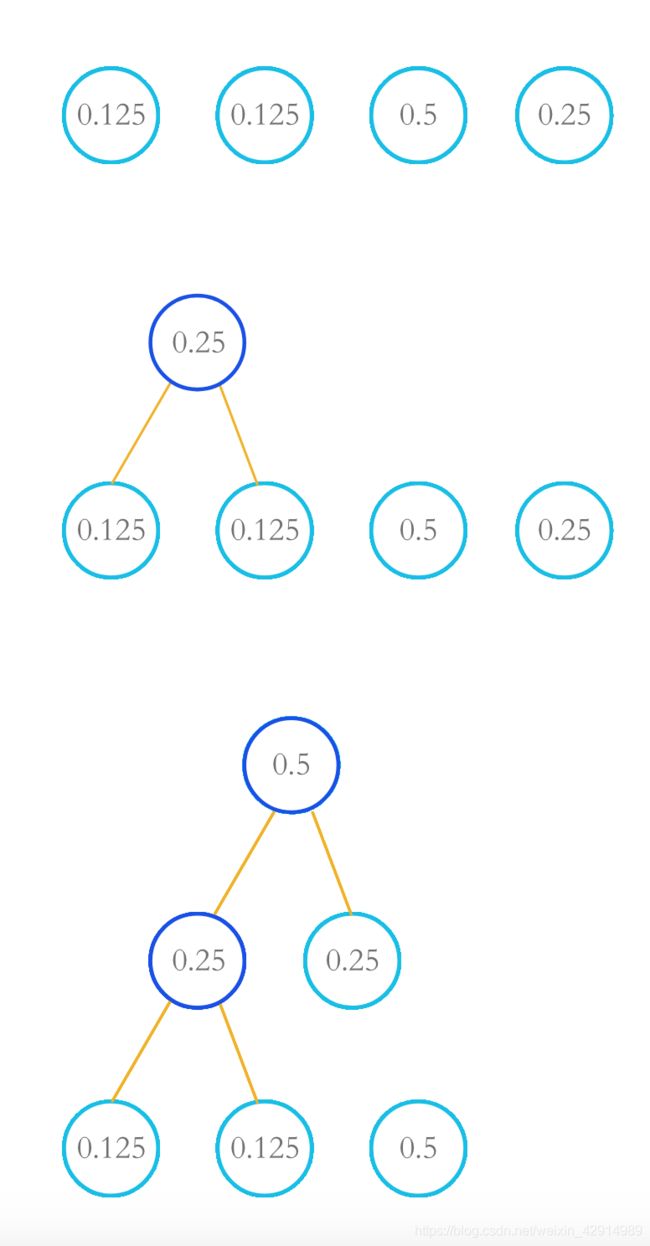
首先将四个概率进行排序，a（0.125）和b（0.125）提取出来相加便成根节点1（0.25），将根节点（0.25）和剩下的c（0.5）、d（0.25）进行新一轮排序；

取最小两值根节点1（0.25）和d（0.25）作为叶子结点相加得到根节点2（0.5）；

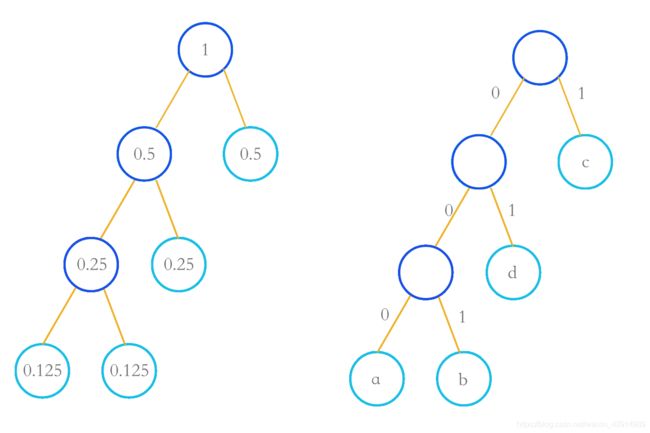
最后队列剩下根节点2（0.5）和c（0.5）相加形成根节点3（1），形成哈夫曼树。

于此，我们可以写出字符abcd的哈夫曼编码分别如下

字符	哈夫曼编码
a	000
b	001
c	1
d	01

（哈夫曼编码结果不唯一，和左右孩子结点编码“0”、“1”有关，本博客默认左孩子结点为“0”，右孩子结点为“1”。）

通过哈夫曼编码所占的内存为3+3+1*2+2=10位。

哈夫曼编码的编码压缩效率

编码压缩效率又称压缩比
$$编码压缩效率=等长码所占内存/哈夫曼编码所占内存$$
如上面所举例子，编码压缩效率：
（5 * 8）/（3+3+1*2+2）= 4

二者相比，使用哈夫曼编码能大大提高编码压缩效率。

通过matlab代码实现哈夫曼编码

思路及代码

• 输入需要编码的文本信息

inData = 'cbacd';  %输入文本

• 对信息进行字符频率统计

%%%字符频率统计
uniqueCharacter=unique(inData);%计算有多少个不重复的字符串
for i=1:length(uniqueCharacter)
uniqueCharacter_num(i)=length(strfind(inData,uniqueCharacter(i))); %统计字符的数目
uniqueCharacter_p(i) = uniqueCharacter_num(i)/length(inData)%不同字符出现的概率
end
uniqueCharacter %显示字符
uniqueCharacter_num %显示个数
uniqueCharacter_p  %显示不同字符出现的概率

• 进行哈夫曼编码

%%创建哈夫曼树
%对字符出现的概率按照从低到高排序
p = uniqueCharacter_p
[a,b]=sort(p); %对p概率矩阵进行排列
m(1,:) = b;
for i = 1:length(a)
    c(i) = uniqueCharacter(b(i));%更新字符队列的排序
end
q = sort(p); %更新概率顺序
n = length(uniqueCharacter_p);
for i = 2:n
    matrix(i-1,2) = c(1);   %在matrix中记录左孩子
    matrix(i-1,3) = c(2);   %在matrux中记录右孩子
    matrix(i-1,1) = double(i-1);                %在matrix中记录根节点
    c(2) = double(i-1);%此处补充数值1，目的是为了以后排序该位置总排在最后，不被处理
    q(2) = q(1) + q(2);     %更新根节点数值
    q(1) = 1;
    %对新的概率组合进行排序   
    [a,b]=sort(q);
    [a1,b1] = sort(b); 
    m(i,:)=b1; %%进行两次sort排记录记录概率对应的位置
    temp_c = c;  %引入中间变量
    temp_q = q;
    for i = 1:length(a1)
         c(i) = temp_c(b(i));%更新字符队列的排序
         q(i) = temp_q(b(i));
         
    end
end

• 读取哈夫曼编码

%读哈夫曼编码
code = uniqueCharacter';
for i = 1:n
    [temp_code,n] = Coding(matrix,uniqueCharacter(i));
    code(i,3:n+2) = temp_code
end

function [code,n] = Coding(matrix,character)
    [a,b] = size(matrix);
    for i = 1:a
        [row,col] = find(matrix(:,2:3)==character);
        character = matrix(row,1);
        if col == 1
            temp_code(i) = '0';
        else
            temp_code(i) = '1';
        end
        code(i) = temp_code(i);
        if row == a
            break
        end
    end
    %此刻需要将编码结果倒转
    temp_code = code;
    n = length(code);
    for i = 1:n
        code(i) = temp_code(length(code)-i+1) ;
    end
end

• 计算编码压缩效率

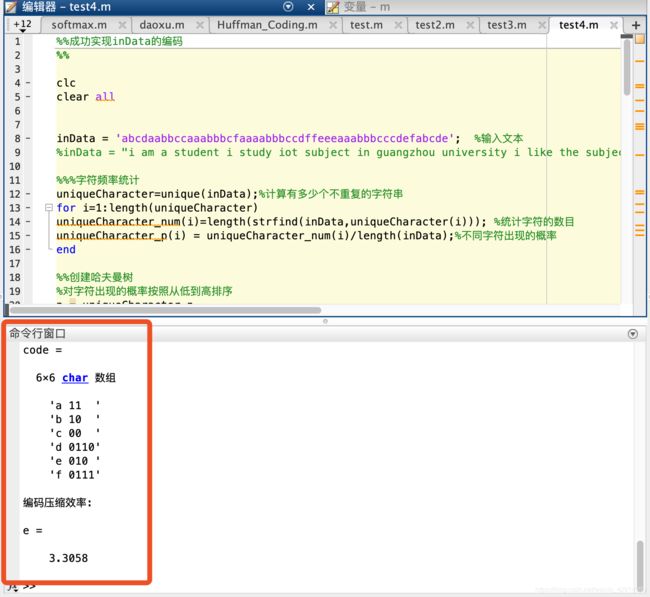
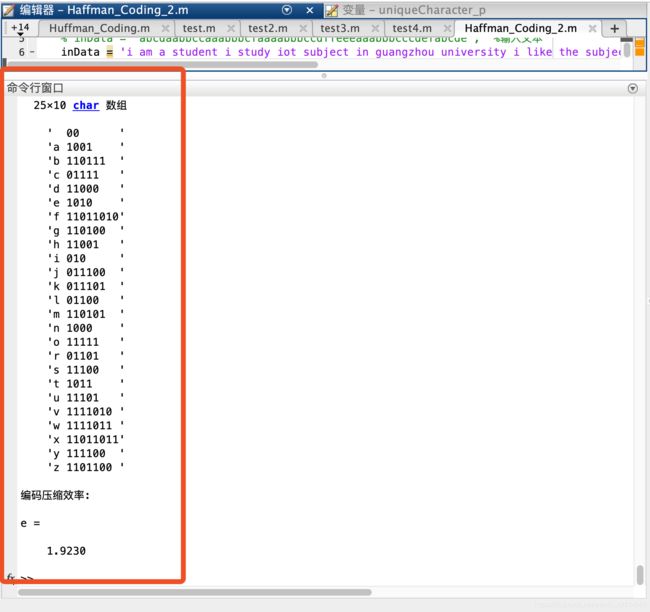
e = (sum(uniqueCharacter_num)*8)/sum(len.*uniqueCharacter_num)

哈夫曼编码实例

完整代码已上传到Github

• 请依据哈夫曼编码的方法对如下的字符进行编码，并计算产生的码流的编码压缩效率:

1. 练习一:“abcdaabbccaaabbbcfaaaabbbccdffeeeaaabbbcccdefabcde”
   
2. 练习二:“i am a student i study iot subject in guangzhou university i like the subject and will work hard and do my best to achieve a high score in final examination”