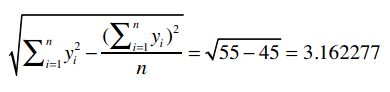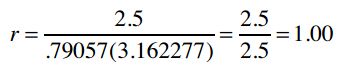文章原创,最近更新:2018-08-31
1.关于本书
2.关于作者
3.内容简介
4.案例
引言:网上找资料觉得这本书挺通俗易懂的,刚好可以跟《机器学习实战》相关章节结合一起学习。
学习参考链接:
1.面向程序员的数据挖掘指南
1.关于本书
写给程序员的数据挖掘实践指南:豆瓣评分:7.4分
作者: [美] Ron Zacharski
出版社: 人民邮电出版社
原作名: A Programmer's Guide to Data Mining
译者: 王斌
出版年: 2015-10-24
2.关于作者
Ron Zacharski是一名软件开发工程师,曾在威斯康辛大学获美术学士学位,之后还在明尼苏达大学获得了计算机科学博士学位。博士后期间,他在爱丁堡大学研究语言学。正是基于广博的学识,他不仅在新墨西哥州立大学的计算研究实验室工作,期间还接触过自然语言处理相关的项目,而该实验室曾被《连线》杂志评为机器翻译研究领域翘楚。除此之外,他还曾教授计算机科学、语言学、音乐等课程,是一名博学多才的科技达人。
3.内容简介
本书是写给程序员的一本数据挖掘指南,可以帮助读者动手实践数据挖掘、集体智慧并构建推荐系统。全书共8章,介绍了数据挖掘的基本知识和理论、协同过滤、内容过滤及分类、算法评估、朴素贝叶斯、非结构化文本分类以及聚类等内容。本书采用“在实践中学习”的方式,用生动的图示、大量的表格、简明的公式、实用的Python代码示例,阐释数据挖掘的知识和技能。每章还给出了习题和练习,帮助读者巩固所学的知识。
4.案例
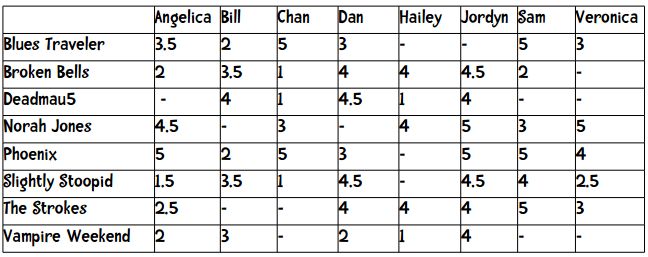
让我们仔细看看用户对乐队的评分,可以发现每个用户的打分标准非常不同:
- Bill没有打出极端的分数,都在2至4分之间;
- Jordyn似乎喜欢所有的乐队,打分都在4至5之间;
- Hailey是一个有趣的人,他的分数不是1就是4。
那么,如何比较这些用户呢?比如Hailey的4分相当于Jordan的4分还是5分呢?我觉得更接近5分。这样一来就会影响到推荐系统的准确性了。
解决方法之一是使用皮尔逊相关系数。简单起见,我们先看下面的数据(和之前的数据不同):
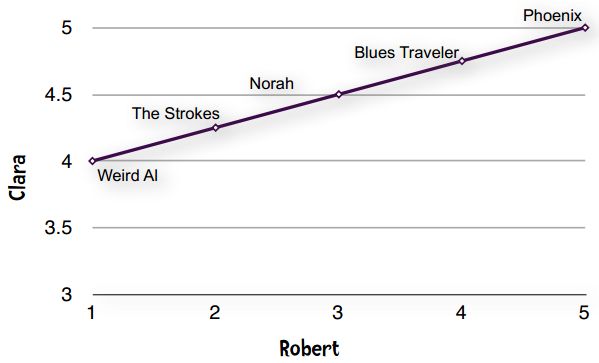
这种现象在数据挖掘领域称为“分数膨胀”。Clara最低给了4分——她所有的打分都在4至5分之间。我们将它绘制成图表:
一条直线——完全吻合!!!
直线即表示Clara和Robert的偏好完全一致。他们都认为Phoenix是最好的乐队,然后是Blues Traveler、Norah Jones。如果Clara和Robert的意见不一致,那么落在直线上的点就越少。
意见基本一致的情形
意见不太一致的情形
所以从图表上理解,意见相一致表现为一条直线。
皮尔逊相关系数用于衡量两个变量之间的相关性(这里的两个变量指的是Clara和Robert),它的值在-1至1之间,1表示完全吻合,-1表示完全相悖。
从直观上理解,最开始的那条直线皮尔逊相关系数为1,第二张是0.91,第三张是0.81。因此我们利用这一点来找到相似的用户。
皮尔逊相关系数的计算公式是:
上面的公式除了看起来比较复杂,另一个问题是要获得计算结果必须对数据做多次遍历。好在我们有另外一个公式,能够计算皮尔逊相关系数的近似值:
这个公式虽然看起来更加复杂,而且其计算结果会不太稳定,有一定误差存在,但它最大的优点是,用代码实现的时候可以只遍历一次数据,我们会在下文看到。
首先,我们将这个公式做一个分解,计算下面这个表达式的值:
对于Clara和Robert,我们可以得到:
很简单吧?下面我们计算这个公式:
Clara的总评分是22.5, Robert是15,他们评价了5支乐队,因此:
所以,那个巨型公式的分子就是70 - 67.5 = 2.5。
下面我们来看分母:
首先:
我们已经计算过Clara的总评分是22.5,它的平方是506.25,除以乐队的数量5,得到101.25。综合得到:
对于Robert,我们用同样的方法计算:
最后得到:
因此,1表示Clara和Robert的偏好完全吻合。
那么如何用代码来表示上述的过程呢?具体如下:
计算皮尔逊相关系数的代码
from math import sqrt
def pearson(rating1, rating2):
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
n = 0
for key in rating1:
if key in rating2:
n += 1
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += pow(x, 2)
sum_y2 += pow(y, 2)
# 计算分母
denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
if denominator == 0:
return 0
else:
return (sum_xy - (sum_x * sum_y) / n) / denominator
测试结果及其代码如下:
pearson(users['Angelica'], users['Bill'])
Out[35]: -0.9040534990682699
pearson(users['Angelica'], users['Hailey'])
Out[36]: 0.42008402520840293
pearson(users['Angelica'], users['Jordyn'])
Out[37]: 0.7639748605475432