概念
PCA(principal components analysis)即主成分分析。主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在统计学中,主成分分析PCA是一种简化数据集的技术。它是一个线性变换的过程。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用于减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
PCA图形的解读
PCA分析虽然朴实无华,其实就是散点图,但它应用十分广泛,能够帮我们解决很多生物学问题。PCA分析应用情境是:在某些情况下,生物数据实在过于复杂。
例如:对一个群体进行重测序,得到的SNP位点数可能是百万级别的。如果我们直接使用百万级别的SNP信息作为指标对个体进行区分,就会显得信息过于庞大而无法把握重点。PCA分析过程就是从这百万级别的信息中提取关键的信息,以便我们使用更少的标记就可以对样本进行有效区分。这些被提取出的信息,按照其效应从大到小排列,我们称之为主成分1(Principal component1)、主成分2、主成分3… …
运用1:群体结构分析
在实际文章中,我们不仅仅使用PC1和PC2来对样本群体进行区分。从数学上理解,PCA分析的过程就是从大量数据指标中提取关键信息的过程。但PC1或PC2对总体信息的解释程度总是有限的。我们将之称为PCn对总体方差解释的百分比。一般重测序的PCA分析结果中,PC1对总体信息的解释比例在3~10%之间。所以,我们也需要关注一下其他主成分的分类效果。
例如在家蚕重测序文章中,分别使用主成分1和2绘图(左图)以及主成分3与主成分4绘图(右图)。两个聚类结果呈现了不同的意义。在PC1和PC2的聚类图中,将野生蚕和家蚕区分开了两个群体。而在PC3和PC4的聚类中,则分离出了两个来自江南地区高产丝量的品种。
所以,从生物学层面理解,PCA分析的过程就是信息浓缩的过程,会从原始的各个SNP位点信息中提取相似的信息,浓缩为新的变量PC1、PC2、PC3…. 输出。所以不同的主成分可能会对应不同的生物学意义,产生不同的聚类分类效果。
运用2:检测离群样本
例如,在上图(右)中,两个高产的品种就属于离群样本。如果你材料已知都是来源同一品种的个体,这种离群样本可能就意味着在采样或测序过程中,出现了样本混淆。如果这些材料后续用于GWAS分析,个别样本出现离群则考虑要把这些离群样本剔除。当然,如果大量样本离群或出现群体分层(例如,上图的左图,明显分层为两个亚群体),则需要将PCA或structure分析的结果作为后续关联分析的协变量,校正它们对关联分析的影响。
运用3:推断进化关系
例如下图这篇葡萄群体研究的文章,研究的葡萄品种来源三个地域。绿色的西部葡萄和红色的东部葡萄区分比较明显,而蓝色的中部葡萄夹杂在东、西两个亚群间,和两个亚群有大量重叠。作者从中推断,东、西两个地域的葡萄都有传播到中部地区,并伴随大量杂交,导致中部地区的品种系谱比较混杂,并没有形成自己独立的亚群。
PCA分析实操
前期准备
给标记加上ID
SNP data通常都是以VCF格式文件呈现,拿到VCF文件的第一件事情就是添加各个SNP位点的ID。
先看一下最开始生成的VCF文件:
可以看到,ID列都是".",需要我们自己加上去。我用的是某不知名大神写好的perl脚本,可以去我的github上下载,用法:
perl path2file/VCF_add_id.pl YourDataName.vcf YourDataName-id.vcf`
当然也可以用excel手工添加。添加后的文件如下图所示(格式:CHROMID__POS):
SNP位点过滤(Missing rate and maf filtering)
SNP位点过滤前需要问自己一个问题,我的数据需要过滤吗?
一般要看后期是否做关联分析(GWAS);如果只是单纯研究群体结构建议不过滤,因为过滤掉低频位点可能会改变某些样本之间的关系;如果需要和表型联系其来做关联分析,那么建议过滤,因为在后期分析中低频位点是不在考虑范围内的,需要保持前后一致。
如果过滤,此处用到强大的plink软件,用法:
plink --vcf YourDataName-id.vcf --maf 0.05 --geno 0.2 --recode vcf-iid -out YourDataName-id-maf0.05 --allow-extra-chr
参数解释:--maf 0.05:过滤掉次等位基因频率低于0.05的位点;--geno 0.2:过滤掉有2%的样品缺失的SNP位点;--allow-extra-chr:我的参考数据是Contig级别的,个数比常见分析所用的染色体多太多,所以需要加上此参数。
格式转换
将vcf文件转换为bed格式文件。
这里注意一点!!!!:应该是软件的问题,需要把染色体/contig名称变成连续的数字(1 to n),不然会报错无法算出结果!(坑)
plink --vcf YourDataName-id-maf0.05.vcf --make-bed --out snp --chr-set 29 no-xy
参数解释:--chr-set 给出染色体/contig的数目;no-xy 没有xy染色体。
用gcta做PCA分析
gcta输出grm阵列(genetic relationship matrix)
gcta64 --make-grm --out snp.gcta --bfile snp --autosome-num 29
参数解释:--autosome-num常染色体数目。
gcta计算PCA
gcta64 --grm snp.gcta --pca 20 --out snp.gcta
参数解读:--pca 20 保留前20个PCA。
特征值结果储存在snp.gcta.eigenval中,特征向量储存在snp.gcta.eigenvec中。
结果处理
将特征值结果和特征向量结果用R处理为可读性结果。写好的R包我放在了Github中:PCA2normal_format.R,大家自行下载使用。
如果不想下载,直接复制如下代码:
eigvec <- read.table("snp.gcta.eigenvec", header = F, stringsAsFactors = F)
write.table(eigvec[2:ncol(eigvec)], file = "gcta.eigenvector.xls", sep = "\t", row.names = F, col.names = T, quote = F)
eigval <- read.table("snp.gcta.eigenval", header = F)
pcs <- paste0("PC", 1:nrow(eigval))
eigval[nrow(eigval),1] <- 0
percentage <- eigval$V1/sum(eigval$V1)*100
eigval_df <- as.data.frame(cbind(pcs, eigval[,1], percentage), stringsAsFactors = F)
names(eigval_df) <- c("PCs", "variance", "proportion")
eigval_df$variance <- as.numeric(eigval_df$variance)
eigval_df$proportion <- as.numeric(eigval_df$proportion)
write.table(eigval_df, file = "gcta.eigenvalue.xls", sep = "\t", quote = F, row.names = F, col.names = T)
转换前snp.gcta.eigenvec
转换后gcta.eigenvector.xls
转换前snp.gcta.eigenval(PCA方差)
转换后gcta.eigenvalue.xls(PCA方差+方差解释率)
用LDAK做PCA分析
相比gcta,能用LD对结果进行校正,具体来说,就是先用LD计算每个SNP位点的权重,根据权重再计算Kinship,这样的结果更接近真实情况。
LDAK输出grm阵列(genetic relationship matrix)
- 在不考虑权重的情况下,方法如下:
ldak5.linux --calc-kins-direct snp.ldak --bfile snp --ignore-weights YES --kinship-gz YES --power -0.25
- 用LD计算每个SNP位点的权重,根据权重再计算Kinship
#切割
ldak5.linux --cut-weights snp.sections --bfile snp
#查看有多少个section
cat snp.sections/section.number
#根据自己的section个数分别计算权重(我这里是31个)
for section in {1..31}; do ldak5.linux --calc-weights snp.sections --bfile snp --section $section; done
#weight文件整合,给SNP赋权重值
ldak5.linux --join-weights snp.sections --bfile snp
#输出grm阵列
ldak5.linux --calc-kins-direct snp.ldak.weight --bfile snp --weights snp.sections/weights.all --kinship-gz YES --power -0.25
LDAK计算PCA(calculate PCA)
- 不考虑权重
ldak5.linux --pca snp.ldak --grm snp.ldak --axes 222
参数解释:--axes 样本数量,这里需要准确填写,不然无法用特征值计算方差解释率。
- 考虑权重
ldak5.linux --pca snp.ldak.weight --grm snp.ldak.weight --axes 222
特征值结果储存在snp.ldak.weight.values中,特征向量储存在snp.ldak.weight.vect中。
结果处理
和gcta方法一样(只是输入文件名称不同),用同一个R包将特征值结果和特征向量结果用R处理为可读性结果,这里不再赘述。
同样,如果不想下载,直接复制如下代码:
eigvec <- read.table("snp.ldak.weight.vect", header = F, stringsAsFactors = F)
colnames(eigvec) <- c("FID", "Sample", paste0("PC", 1:20))
write.table(eigvec[2:ncol(eigvec)], file = "ldak.eigenvector.xls", sep = "\t", row.names = F, col.names = T, quote = F)
eigval <- read.table("snp.ldak.weight.values", header = F)
pcs <- paste0("PC", 1:nrow(eigval))
eigval[nrow(eigval),1] <- 0
percentage <- eigval$V1/sum(eigval$V1)*100
eigval_df <- as.data.frame(cbind(pcs, eigval[,1], percentage), stringsAsFactors = F)
names(eigval_df) <- c("PCs", "variance", "proportion")
eigval_df$variance <- as.numeric(eigval_df$variance)
eigval_df$proportion <- as.numeric(eigval_df$proportion)
write.table(eigval_df, file = "ldak.eigenvalue.xls", sep = "\t", quote = F, row.names = F, col.names = T)
数据可视化
用R画散点图即可,散点图的画法由于篇幅原因,另外写个帖详细说明。这里直接分享一下我作图的方法:
数据准备
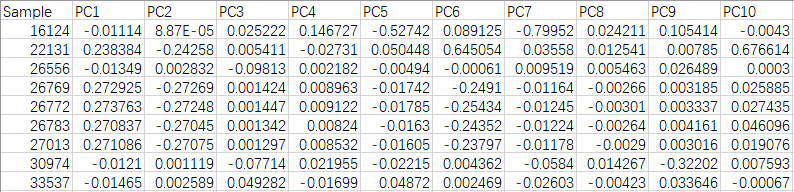
除了上面获得的两个文件:ldak.eigenvector.xls和ldak.eigenvalue.xls外,还需要准备一个命名为pca.pop.xls的文件,该文件包含如下内容:
注:第一列为排序;第二列为ID+vcf_id;第三列为vcf_id,需要和ldak.eigenvector.xls文件中SampleI ID一致;第四列为分组信息1;第五列为基于分组信息1给予的颜色信息;第六列为基于分组信息2给予的标记形状信息;第七列为分组信息2(例子中为地理来源)。
赋值
按照如下代码给各个参数赋值(赋予路径信息):
eigvec <- "E:/Desktop/PCA/ldak.eigenvector.xls"
eigval <- "E:/Desktop/PCA/ldak.eigenvalue.xls"
popinfo <- "E:/Desktop/PCA/pca.pop.xls"
key <- "ldak_PCA"
od <- "E:/Desktop/PCA"
注:我在桌面建了一个名为PCA的文件夹,把ldak.eigenvector.xls、ldak.eigenvalue.xls和pca.pop.xls三个文件都放在里面;key是指定输出文件的文件名前缀;od是指定输出文件存放目录。
调用pca.plot2d.r包作图
poptable <- read.table(popinfo, header = T, comment.char = "")
pop <- unique(poptable[,4:7])
print(pop)
source("pca.plot2d.r")
pca_plot(eigenvector = eigvec, eigenvalue = eigval,
group = popinfo, key = key, outdir = od,
shape = T, shapes = pop$pch, border = T, border_size = 2.5,
line0 = T, line0_size = 1)
执行后会返回,分别以PC1-PC2、PC1-PC3和PC2-PC3为坐标轴的PCA图,包括pdf和png两种格式的文件。
注:我用的是我自己的数据,因为还未发表,所以我隐藏了图例,大家执行之后图片是会有图例的。
参考:
群体结构图形三剑客——PCA图
Xia Q, Guo Y, Zhang Z, et al.Complete resequencing of 40 genomes reveals domestication events and genes insilkworm (Bombyx)[J]. Science, 2009, 326(5951): 433-436.
Myles S, Boyko A R, Owens C L, et al. Genetic structure and domesticationhistory of the grape[J]. Proceedings of the National Academy of Sciences, 2011,108(9): 3530-3535.
基迪奥全基因组关联分析(GWAS)