【Leetcode 二叉树系列】144.二叉树的前序遍历 Python3 迭代和递归

题目链接：
力扣_144.二叉树的前序遍历

二叉树的前序遍历的方式是根左右的顺序，那么优先选取递归的方式来做，之后再考虑是否可以用迭代的方式来完成

1.递归

一般很顺的递归的前序遍历都是print的方式，不需要考虑保存结点值，就能很快写出很基础的代码：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return
        print(root.val)
        self.preorderTraversal(root.left)
        self.preorderTraversal(root.right)

这个是一个很原始的模板，现在题目要求要返回这个树的前序遍历的结点值的数组，那么我们需要用一个数组来保存这个结果，就需要在这个模板上进行对应的修改

怎么修改呢？我们要用一个list来不停的append新的结点值，那么这个方法的入参就需要传入这样的一个list，并且这个方法返回的值也应该是这个list，那么我们就应该新写一方法来承载这两个入参，原函数就应该调用这个新的方法，传入root和一个初始化的数组res，然后在新的方法里更新这个res，在原方法里最终返回这个数组，（这个数组传入新函数之后一直在更新，所以不需要用一个返回值来接收，可以直接返回这个变量），

然后应该在新的方法里面去递归遍历并传入更新后的res，把print的那一行改为累加结点值res.append(root.val)以达到保存所有结点值的效果

那么我们现在基本框架就搭建好了：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        # if not root 这一步在preOrder里面做了
        res = []
        self.preOrder(root, res)

        return res

    def preOrder(self, root, res):
        '''对root的判空其实是在这里做了，所以原方法就不需要对root再一次判空'''
        if not root:
            return res
        res.append(root.val)
        self.preOrder(root.left, res)
        self.preOrder(root.right, res)
        
        return res

2.迭代

递归的相对来说很好考虑和写代码，那么能不能用迭代的方式来做呢？
迭代的时候优先考虑用栈模拟递归的方式，那么这里就有一点需要注意，前序遍历是根左右的顺序，但是栈是后进先出的顺序，需要多注意一下

如何模拟呢？我首先需要一个栈来保存我遍历的结点顺序，这个栈的初始值应该为stack = [root] if root，还需要另外一个栈来保存我的前序遍历的结果：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        
        if not root:
            return []
        
        stack = [root]  # 保存遍历结点
        res = []  # 保存遍历的结果

那我如何去迭代呢，迭代的条件是什么呢？肯定是当我没有结点可以继续遍历的时候，就终止遍历，也就是while stack的时候我需要继续遍历，每一次的遍历通过stack.pop()来获取要遍历的结点，遍历之后需要添加当前节点的左右子节点至stack中，直到stack为空就跳出循环，返回结果

那么在遍历的内部应该如何同步更新stack和res呢？

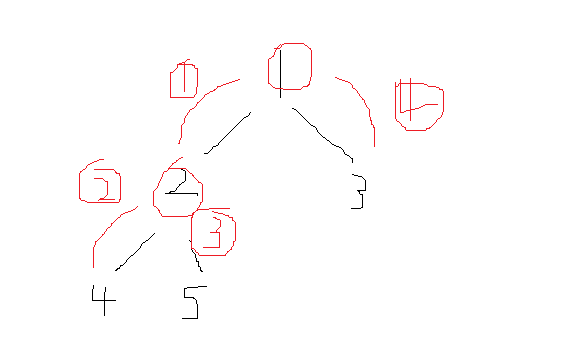
如图：前序遍历的顺序应该是1,2,4,5,3，那么我想要一直把左节点遍历完全之后再考虑右节点，但是在保存每个结点的左右子树的时候，需要同时判断和同时添加，那么这时候就利用栈的后进先出的特点来完成这样的一个操作：遍历的时候将root.val添加至res结果数组内，然后顺序添加root.right和root.left

为什么要先添加右子树再添加左子树呢？因为我每次从stack里pop出来的是后添加的点，我又需要先获得左节点，那么就应该后append左节点，并且每次在遍历完当前点之后，pop获得的仍然是左节点，直到左节点都pop完全，才会pop出第一个右节点
如：

stack=[1], res=[]
node = stack.pop() = 1, stack = [3,2], res = [1]
node = stack.pop() = 2, stack = [3,5,4], res = [1,2]
node = stack.pop() = 4, stack = [3,5], res = [1,2,4]
'''以此类推，stack这样右左的append顺序，能够拿到左右的pop顺序'''

那么我们就可以在while的循环内部去完善我们的代码了：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        
        if not root:
            return []
        
        stack = [root]
        res = []
        
        while stack:
            node = stack.pop()
            res.append(node.val)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        
        return res

3.叨叨

现在留点坑坑给自己叨两句吧，今天啥也没干，遇到一道路径总和III的题，让我怀疑人生，于是跑回来看递归，然后递归又让我先看二叉树，于是先写这么一个二叉树系列吧。
计划了很多要做的，但是重点还是得去做，现在已经11月的第一天了，希望今天能收到一个好消息，拜托了。明天继续1234的TODO list的遍历吧。

4.新思路【简直不要太妙】

【叨叨：今天是11.04号，我确实在11月的第一天收到了好消息，我终于可以去北京啦！！！那么还愿的同时还得更珍惜更努力！！！写题解不能停！！！！】

• 尾递归：是递归调用在递归实例体的尾部，这样的递归很容易化解为迭代，需要引入一个辅助栈即可

今天继续在看二叉树，废了好多天在激动开心和王者大峡谷（已删游戏保平安…），回来继续看二叉树的时候，发现中序遍历的迭代很难自己去思考，那么就又回顾了一下前序遍历的迭代实现，但在学习的过程中，发现了一个新思路，此处吹爆清华教授邓俊辉老师【膜拜一下男神】

新思路是啥呢？

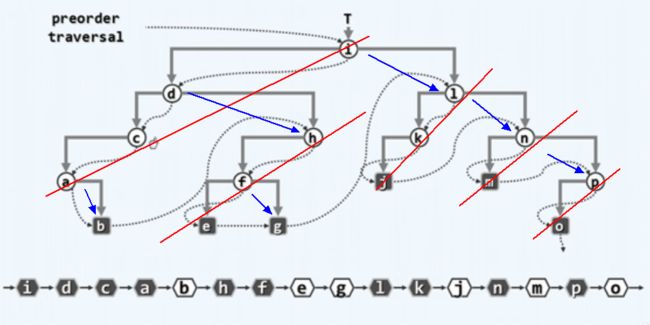
从图中可以看出来，我们前序遍历的时候，其实是从一个节点开始，先自上往下遍历了一整条它的左侧孩子链，也就是i->d->c->a，然后再自下往上的遍历了这些左侧孩子链的右孩子链，也就是如下图所示：
并且这里我们用到栈，实际上也是利用了栈的先进后出的特点，能够让先添加的右孩子在最后被遍历到（比如1的这个右孩子，其实应该是从d开始遍历到3然后2最后还遍历到1）

所以这个新思路也就是：自上往下的遍历左孩子链，自下往上的添加右孩子链，那么我们需要一个辅助栈来保存需要遍历的节点，还需要一个数组来保存遍历的结果，并且对于遍历左孩子链，我们应该单独写一个方法来实现：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        '''分摊O(1)'''
        if not root:
            return []
        
        stack = [root]  # 辅助栈保存遍历节点
        visit = []  # 保存遍历结果
        
        while stack:
            '''对于每一个节点，都是从辅助栈中pop而来，然后去遍历它的左孩子链，在遍历的同时需要更新辅助栈和保存遍历结果'''
            node = stack.pop()
            self.visitLeftBranch(node, stack, visit)
            
        return visit
        
    
    def visitLeftBranch(self, node, stack, visit):
        '''#pop = #append = #visit = O(n) = 分摊O(1)'''
        
        while node:
            visit.append(node.val)
            if node.right:
            '''在每一次遍历左孩子链的同时，都需要把右孩子更新到辅助栈中'''
                stack.append(node.right)
            node = node.left

这是c++代码重写而来的，这样写其实Python会很慢，于是做了如下的更新：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        
        stack = []
        visit = []
        node = root
        
        while node or stack:
            '''这其实就是在对于每个节点，遍历它的左孩子链，并且在遍历的过程中，保存遍历的结果
            并且在每遍历一个左节点的时候，都添加它的右孩子到辅助栈中'''
            while node:
                visit.append(node.val)
                stack.append(node.right)
                node = node.left
            node = stack.pop()
            
        return visit