力扣刷题笔记

参考链接：图解算法数据结构

代码和思路主要来源：

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/
来源：力扣（LeetCode）

动态规划

剑指Offer 58 - Ⅱ.左旋转字符串

四种解题思路

1. 字符串切片(简单效率高)

class Solution {
public:
    string reverseLeftWords(string s, int n) {
        return s.substr(n, s.size()) + s.substr(0, n);
    }
};

2. 列表、字符串遍历拼接
   原理类似：通过新建list或者string变量res，先向res添加“第n + 1位至末位的字符”，再向 res 添加 “首位至第n位的字符” ，最后将res转化为字符串并返回。

3. 三次翻转(C++)
   由于C++中的字符串是可变类型，因此可在原字符串上直接操作实现字符串旋转，实现O(1)的空间复杂度。

class Solution {
public:
    string reverseLeftWords(string s, int n) {
        //使用双向迭代器的重排算法，reverse(beg, end)
        reverse(s.begin(), s.begin() + n);
        reverse(s.begin() + n, s.end());
        reverse(s.begin(), s.end());
        return s;
    }
};

剑指Offer 67 - 把字符串转换成整数

主站第8题

先贴代码

class Solution {
public:
    int strToInt(string str) {
        int res = 0, bndry = INT_MAX / 10;	// 变量初始化
        int i = 0, sign = 1, length = str.size();	// 默认sign为正
        if(length == 0) return 0;	// 若为空字符串，直接返回0
        while(str[i] == ' ')	// 先判断字符串开头是否为空格，若为true则进入if语句
            if(++i == length) return 0;	// i+1后是否已经到达字符串尾部，若为true,返回0
        if(str[i] == '-') sign = -1;	// 开始判断正负号，已经默认为正了，所以仅作负号判断即可
        if(str[i] == '-' || str[i] == '+') i++;	// 符号位判断结束，i+1开始遍历
        for(int j = i; j < length; j++) {	// 临时变量j，遍历字符串
            if(str[j] < '0' || str[j] > '9') break;	// 每次循环先判断当前字符是否不是数字，若为true，直接跳出循环
            if(res > bndry || res == bndry && str[j] > '7')	// 拼接前，判断是否会越界，若为true，返回
                return sign == 1 ? INT_MAX : INT_MIN;
            res = res * 10 + (str[j] - '0'); // 拼接，10进制
        }
        return sign * res;	// 结束符号位，返回数值
    }
};

考虑四种字符：

1. 首部空格：直接删除；
2. 符号位，利用一个int变量sign保存符号位，默认为正，取值为1，若为负，取值为-1，在返回前做正负判断，即在代码最后乘上sign；
3. 非数字字符：碰到首个非数字的字符时，立即返回；
4. 数字字符：
   1. 字符转数字：此数字的ASCII码与0的ASCII码相减即可，(str[j] - '0');
      2. 数字拼接：从左向右遍历数字，res = res * 10 + (str[j] - '0');

数字越界处理：

在每轮数字拼接前，判断res在此轮拼接后是否超过2147483647，若超过则加上符号位直接返回。

设数字拼接编辑 bndry = 2147483647 // 10 = 214748364，则有以下两种情况越界：

​ res > bndry 情况一：执行拼接10×res≥2147483650越界
​ res = bndry, x > 7 情况二：拼接后是2147483648或2147483649越界

​ if(res > bndry || res == bndry && str[j] > '7')

剑指Offer 10-Ⅰ. 斐波那契数列

1. 递归解决，因为当n很大的时候可能会出现数字溢出，所以我们需要用结果对1000000007求余。如果直接对最后的结果求余会有一个问题，即可能还没执行到最后一步就已经溢出了，所以需要对每一步的计算都求余。但由于这样递归的时候会造成大量的重复计算，所以运行起来会超时。

class Solution{
public:
    int fib(int n){
        if(n < 2) return n;
        int first = fib(n - 1) % 1000000007;
        int second = fib(n - 2) % 1000000007; 
        return (first + second) % 1000000007;
    }
}

2. 为了避免重复计算，可以使用一个关联容器map把计算过的值保存，每次计算的时候先从map中查找有没有。

int constant = 1000000007;

public int fib(int n) {
    return fib(n, new HashMap());
}

public int fib(int n, Map map) {
    if (n < 2)
        return n;
    if (map.containsKey(n))
        return map.get(n);
    int first = fib(n - 1, map) % constant;
    map.put(n - 1, first);
    int second = fib(n - 2, map) % constant;
    map.put(n - 2, second);
    int res = (first + second) % constant;
    map.put(n, res);
    return res;
}
作者：sdwwld
链接：https://leetcode-cn.com/problems/fei-bo-na-qi-shu-lie-lcof/solution/di-gui-he-fei-di-gui-liang-chong-fang-shi-du-ji-ba/

3. 推荐做法：非递归做法，动态规划
   • 状态定义：设dp为一维数组，其中dp[i]的值代表斐波那契数列的第i个数字
   • 转移方程：dp[i + 1] = dp[i] + dp[i - 1]，即对应数列定义f(n + 1) = f(n) + f(n - 1);
   • 初始状态： dp[0] = 0，dp[1] = 1，即初始化前两个数字;
   • 返回值：dp[n]，即斐波那契数列的第n个数字。

public int fib(int n) {
    int constant = 1000000007;
    int a = 0;
    int b = 1;
    for(int i = 0;i < n; i++) {
        int sum = (a + b) % constant;	//先求和,求余法则(x+y)⊙p=(x⊙p+y⊙p)⊙p 
        a = b;	
        b = sum;
    }
    return a;  //为什么要返回a呢？可以自己手写下，当n等于4的时候，返回a的值是5，但sum是8，所以返回a的值才是对的。
}

剑指Offer 10- Ⅱ.青蛙跳台阶问题

动态规划：

若f(x)表示爬到第x级台阶的方案数，由于最后一步可能跨了一级台阶，也可能跨了两级台阶，所以转移方程为：
$$f(x)=f(x-1)+f(x-2)$$
边界条件：爬第0级可以看作只有一种方案，即f(0) = 1；从0级到第1级也只有一种方案，即爬一级，f(1) = 1。

优化：由于f(x) 只和 f(x - 1)与 f(x - 2)有关，所以可以用「滚动数组思想」把空间复杂度优化成 O(1)。

class Solution {
public:
    int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            r = p + q;
        }
        return r;
    }
};

剑指Offer 42 - 连续子数组的最大和

标准动态规划解题流程：

1. **状态定义：**设动态规划列表dp，dp[i]代表以元素nums[i]为结尾的连续子数组最大和。

   为何定义最大和dp[i]中必须包含元素nums[i]：保证dp[i]递推到dp[i+1]的正确性；如果不包含nums[i]，递推时则不满足题目的连续子数组要求。

2. **转移方程：**若dp[i - 1] ≤ 0，说明dp[i - 1]对dp[i]产生负贡献，即dp[i- 1]+nums[i]还不如nums[i]本身大。
   $$dp[i]=\{\begin{array}{r}dp[i-1]+nums[i],dp[i-1]>0\\ nums[i],dp[i-1]\le 0\end{array}$$

3. 初始状态: dp[0] = nums[0]，即以nums[0]结尾的连续子数组最大和为nums[0]。

4. **返回值：**返回dp列表中的最大值。

由于 dp[i]只与 dp[i-1]和nums[i]有关系，因此可以将原数组 nums用作 dp列表，即直接在 nums上修改即可。降低至空间复杂度O(1)。

class Solution{
public:
    int maxSubArray(vector& nums){
        int res = nums[0];
        for(auto i = 1; i < nums.size(); i++){
            if(nums[i - 1] > 0) nums[i] += nums[i - 1];
            if(nums[i] > res) res = nums[i];
        }
        return res;
    }
}

剑指Offer 46 - 把数字翻译成字符串

转移方程：

动态规划解析：

记数字$num$第$i$位数字为$ x_i $,数字$num$的位数为$n$；

例如：$num=12258$的$n=5,x1=1$

• 状态定义： 设动态规划列表$ dp，dp[i]$代表以$x_i$为结尾的数字的翻译方案数量。

• **转移方程：**若$x_i$和$x_i-1$组成的两位数字可被整体翻译，则$dp[i]=dp[i-1]+dp[i-2]$，否则$dp[i]=dp[i-1]$。
  $$dp[i]=\{\begin{array}{r}dp[i-1]+dp[i-2],(10x_{i-1}+x_i)\in [10,25]\\ dp[i-1]，(10x_{i-1}+x_i)\in [0,10)\bigcup (25,99]\end{array}$$

  可被整体翻译的两位数区间分析： 当 $x_{i-1}=0$ 时，组成的两位数无法被整体翻译（例如 00, 01, 02,⋯ ），大于 25的两位数也无法被整体翻译（例如 26, 27,⋯ ），因此区间为$ [10, 25] $。

• 初始状态：$dp[0]=dp[1]=1$，即“无数字”和“第1位数字”的翻译方法数量均为1；

• 返回值：$dp[n]$，即此数字的翻译方案数量;

class Solution {
public:
    int translateNum(int num) {
        string s = to_string(num); //将数字转化为字符串，方便获取数字的各位x_i，通过遍历s实现动态规划
        int a = 1, b = 1, len = s.size();
        for(int i = 2; i <= len; i++) {
            string tmp = s.substr(i - 2, 2);
            int c = tmp.compare("10") >= 0 && tmp.compare("25") <= 0 ? a + b : a;
            b = a;
            a = c;
        }
        return a;
    }
};

剑指Offer 47 - 礼物的最大价值

解题思路：

根据题目说明，得到某单元格只可能从上边单元格或左边单元格到达。

设$ f(i, j) $ 为从棋盘左上角走至单元格$ (i, j) $的礼物最大累计价值，易得到以下递推关系：$ f(i, j)$ 等于$ f(i, j - 1) $ 和 $ f(i - 1, j) $ 中的较大值加上当前单元格礼物价值$ grid(i, j) $。
$$f(i,j)=max[f(i,j-1),f(i-1,j)]+grid(i,j)$$
因此，可用动态规划解决此问题，以上公式编为转移方程。

**状态定义：**设动态规划矩阵$ dp$，$dp(i,j)$代表从棋盘的左上角开始，到达单元格$ (i,j)$时能拿到礼物的最大累计价值。

转移方程：

1. 当 i = 0 且 j = 0 时，为起始元素；

2. 当 i = 0 且 j ≠ 0 时，为矩阵第一行元素，只可从左边到达;

3. 当 i ≠ 0 且 j ≠ 0 时，为矩阵第一列元素，只可从上边到达；

4. 当 i ≠ 0 且 j ≠ 0 时，可从左边或上边到达；
   $$dp(i,j)=\{\begin{array}{r}grid(i,j),i=0,j=0\\ grid(i,j)+dp(i,j-1),i=0,j\ne 0\\ grid(i,j)+dp(i-1,j),i\ne 0,j=0\\ grid(i,j)+max[dp(i-1,j),dp(i,j-1)],i\ne 0,j\ne 0\end{array}$$

初始状态：$dp[0][0]=grid[0][0]$，即到达单元格(0, 0)时能拿到礼物的最大累计价值为$grid[0][0]$；

返回值：$dp[m-1][n-1]$，m, n分别为矩阵的行高和列宽，即返回$dp$矩阵右下角元素。

空间复杂度降低：

• 由于$ dp[i][j]$只与$dp[i - 1][j], dp[i][j - 1], grid[i][j]$有关系，因此可以将原矩阵grid用作dp矩阵，即直接再grid上修改即可。
• 应用此方法可省去$dp$矩阵使用的额外空间，因此空间复杂度从O(MN)降至O(1)。

class Solution {
public:
    int maxValue(vector>& grid) {
        int m = grid.size(), n = grid[0].size();
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(i == 0 && j == 0) continue;
                if(i == 0 && j != 0) {
                    grid[i][j] += grid[0][j - 1];
                    continue;
                }
                if(i != 0 && j == 0){
                    grid[i][j] += grid[i - 1][0];
                    continue;
                }
                grid[i][j] += max(grid[i][j - 1], grid[i - 1][j]);
            }
        }
        return grid[m - 1][n - 1];
    }
};

剑指Offer 48 - 最长不含重复字符子串

请注意理解题目：是找无重复字符！

长度为N的字符串公有$ \frac{(1+N)(N)}{2} $个子字符串（复杂度为$O(N^{2)$），判断长度为N的字符串是否有重复字符的复杂度为$O(N)$，因此本题使用暴力法解决的复杂度为$O(N}3)$。考虑使用动态规划降低时间复杂度。

动态规划解析：

• **状态定义：**设动态规划列表$dp$，$dp[j]$代表以字符$s[j]$为结尾的"最长不重复子字符串"的长度。

• **转移方程：**固定右边界$j$，设字符$s[j]$左边距离最近的相同字符为$s[i]$，即$s[i]=s[j]$。

  1. 当$i<0$，即$s[j]$左边无相同字符，则$dp[j]=dp[j-1]+1$;
  2. 当$dp[j-1]<j-i$，说明字符$s[i]$在子字符串$dp[j-1]$区间之外，则$dp[j]=dp[j-1]+1$;
  3. 当$dp[j-1]\ge j-i$，说明字符$s[i]$在子字符串$dp[j-1]$区间之中，则$dp[j]$的左边界由$s[i]$决定，即$dp[j]=j-i$；

当$i<0$时，由于$dp[j - 1] ≤ j $恒成立，因而$dp[j - 1] < j - i$恒成立，因此分支1.和2.可被合并。

$$dp[j]=\{\begin{array}{r}dp[j-1]+1,dp[j-1]<j-i\\ j-i,dp[j-1]\ge j-i\end{array}$$

• 返回值：$max(dp)$，即全局的”最长不重复子字符串“的长度。

  

空间复杂度降低：

• 由于返回值是取$dp$列表最大值，因此可借助变量$tmp$存储$dp[j]$，变量$res$每轮更新最大值即可。
• 此优化可节省$dp$列表使用的$O(N)$大小的额外空间。

待解决问题：每轮遍历字符$s[j]$时，如何计算索引$i$？

方法一：动态规划 + 哈希表

• 哈希表统计：遍历字符串$s$时，使用哈希表（记为$dic$）统计各字符最后一次出现的索引位置。
• **左边界i获取方式：**遍历到$s[j]$时，可通过访问哈希表$dic[s[j]]$获取最近的相同字符的索引$i$。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map dic;
        int res = 0, tmp = 0, len = s.size(), i = -1;
        for(int j = 0; j < len; j++){
            if(dic.find(s[j]) == dic.end()) i = -1;
            else i = dic.find(s[j])->second; // 获取索引i
            dic[s[j]] = j;	// 更新哈希表
            tmp = tmp < j - i? tmp + 1: j - i;
            res = max(res, tmp);
        }
        return res;
    }
};

方法二：动态规划 + 线性遍历

• **左边界$i$获取方式：**遍历到$s[j]$时，初始化索引$i=j-1$，向左遍历搜索第一个满足$s[i]=s[j]$的字符即可。

class Solution{
public:
	int lengthOfLongestSubstring(string s){
        int res = 0, tmp = 0, len = s.size();
        for(int j = 0; j < len; j++){
            int i = j - 1;
            while(i >= 0 && s[i] != s[j]) i--;	//线性查找
            tmp = tmp < j - i ? tmp + 1: j - i;	//dp[j - 1]->dp[j]
            res = max(res, tmp);	//max(dp[j-1], dp[j])
        }
        return res;
    }
}

方法三：双指针 + 哈希表

• **哈希表$dic$统计：**指针$j$遍历字符$s$，哈希表统计字符$s[j]$最后一次出现的索引。

• **更新左指针i：**根据上轮左指针$i$和$dic[s[j]]$，每轮更新左边界$i$，保证区间$[i+1,j]$内无重复字符且最大。
  $$i=max(dic[s[j]],i)$$

• **更新结果$res$：**取上轮$res$和本轮双指针区间$[i+1，j]$的宽度（即$j-i$）中的最大值。
  $$res=max(res,j-i)$$

class Solution{
public:
	int lengthOfLongestSubstring(string s){
		unordered_map dic;
        int i = -1, res = 0, len = s.size();
        for(int j = 0; j < len; j++){
            if(dic.find(s[j]) != dic.end())
                i = max(i, dic.find(s[j])->second);	// 更新左指针
            dic[s[j]] = j;	// 更新哈希表记录
            res = max(res, j - i);	// 更新结果
        }
        return res;
    }
}

剑指Offer 49 - 丑数

参考：

作者：LZH_Yves
链接：https://leetcode-cn.com/problems/ugly-number-ii/solution/bao-li-you-xian-dui-lie-xiao-ding-dui-dong-tai-gui/

题目描述：只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

解题思路：

抽数的递推性质：丑数只包含因子2，3，5，因此有"丑数=某较小丑数 x 某因子"（例如：10 = 5 x 2）。

设已知长度为$n$的丑数序列$x_1,x_2,...,x_n$，求第n+1个丑数$x_{n+1}$。根据递推性质，丑数$x_{n+1}$只可能是以下三种情况其中之一（索引a,b,c为未知数）：
$$x_{n+1}=\{\begin{array}{r}{x}_a\times 2,a\in [1,n]\\ x_b\times 3,b\in [1,n]\\ x_c\times 5,c\in [1,n]\end{array}$$
方法一：暴力法(brute force)

为啥我脑子里得暴力法是拿一个个数去除，人家想的就不一样，菜的扣脚！

class Solution{
public:
    int nthUglyNumber(int n){
        vector v;
        for(long long a = 1; a <= INT_MAX; a = a * 2)
            for(long long b = a; b <= INT_MAX; b = b * 3)
                for(long long c = b; c <= INT_MAX; c = c * 5)
                    v.push_back(c);
        sort(v.begin(), v.end());
        return v.at(n - 1);
    }
};

方法二：动态规划

丑数递推公式：若索引a,b,c满足以上条件，则下个丑数$x_{n+1}$为以下三种情况中的最小值：
$$x_{n+1}=min(x_a\times 2,x_b\times 3,x_c\times 5)$$
由于$x_{n+1}$是最接近$x_n$的丑数，因此索引a,b,c需满足以下条件：
$$\{\begin{array}{r}{x}_a\times 2>x_n\ge x_{a-1}\times 2,即x_a为首个乘以2后大于x_n的丑数\\ x_b\times 3>x_n\ge x_{b-1}\times 3,即x_b为首个乘以3后大于x_n的丑数\\ x_c\times 5>x_n\ge x_{c-1}\times 5,即x_c为首个乘以5后大于x_n的丑数\end{array}$$

设置指针a，b，c指向首个丑数（即1），循环根据递推公式得到下个丑数，并每轮将对应指针执行+1即可。

• **状态定义：**设动态规划列表$dp$，$dp[i]$代表第$i+1$个丑数；

• 转移方程：

  1. 当索引$a,b,c$满足以下条件时，$dp[i]$为三种情况的最小值；

  2. 每轮计算$dp[i]$后，需要更新索引$a,b,c$的值，使其始终满足方程条件。实现方法：分别独立判断$dp[i]$和$dp[a]\times 2$，

     $dp[b]\times 3$，$dp[c]\times 5$ 的大小关系，若相等则将对应索引a，b，c加1；
     $$\{\begin{array}{r}dp[a]\times 2>dp[i-1]\ge dp[a-1]\times 2\\ dp[b]\times 3>dp[i-1]\ge dp[b-1]\times 3\\ dp[c]\times 3>dp[i-1]\ge dp[c-1]\times 3\end{array}$$

• 初始状态：$dp[0]=1$，即第一个丑数为1；

• 返回值：$dp[n-1]$，即返回第n个丑数。

class Solution{
public:
    int nthUglyNumber(int n){
        int a = 0, b = 0, c = 0;
        int dp[n];
        dp[0] = 1;
        for(int i = 1; i < n; i++){
            int n2 = dp[a] * 2, n3 = dp[b] * 3, n5 = dp[c] * 5;
            dp[i] = min(min(n2, n3), n5);
            if(dp[i] == n2) a++;
            if(dp[i] == n3) b++;
            if(dp[i] == n5) c++;
        }
        return dp[n - 1];
    }
};

方法三：优先队列(小顶堆)

利用优先队列有自动排序的功能
每次取出队头元素，存入队头元素*2、队头元素*3、队头元素*5
但注意，像 12 这个元素，可由 4 乘 3 得到，也可由 6 乘 2 得到，所以要注意去重

class Solution {
public:
    int nthUglyNumber(int n) {
        priority_queue ,greater > q; // 一定要有空格，不然成了右移运算符
        double answer=1;
        for (int i=1;i,greater > q;
        set s;
        s.insert(1);
        vector mask({2,3,5});
        double answer=1;
        for (int i=1;i

剑指Offer 63 - 股票的最大利润

动态规划解析：

• **状态定义：**设动态规划列表$dp$，$dp[i]$代表以$prices[i]$为结尾的子数组的最大利润（以下简称为前$i$日的最大利润）。

• **转移方程：**由于题目限定“买卖该股票一次”，因此前i日最大利润$dp[i]$等于前$i-1$日最大利润$dp[i-1]$和第$i$日卖出的最大利润中的最大值。
  $$dp[i]=max(dp[i-1],prices[i]-min(prices[0:i]))$$

• 初始状态：$dp[0]=0$，即首日利润为0；

• 返回值：$dp[n-1]$，其中$n$为$dp$列表长度。

  

时间复杂度降低：

前i日的最低价格$min(prices[0:i])$时间复杂度为$O(i)$。而在遍历$prices$时，可以借助一个变量（记为成本$cost$）每日更新最低价格。优化后的转移方程为：
$$dp[i]=max(dp[i-1],prices[i]-min(cost,prices[i]))$$
空间复杂度降低：

由于$dp[i]$只与$dp[i-1],prices[i],cost$相关，因此可使用一个变量（记为利润$profit$）代替$dp$列表。优化后的转移方程为：
$$profit=max(profit,prices[i]-min(cost,prices[i]))$$

class Solution {
public:
    int maxProfit(vector& prices) {
        int cost = INT_MAX, profit = 0;
        for(int price : prices) {
            cost = min(cost, price);
            profit = max(profit, price - cost);
        }
        return profit;
    }
};

搜索与回溯算法

剑指Offer 12 - 矩阵中的路径

典型的矩阵搜索问题，可使用深度优先搜索(DFS)+剪枝。

• **深度优先搜索：**可以理解为暴力法遍历矩阵中所有字符串可能性。DFS通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
• 剪枝：在搜索中，遇到这条路不可能和目标字符串匹配成功的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为可行性剪枝。

DFS解析：

• **递归参数：**当前元素在矩阵board中的行列索引i和j，当前目标字符在word中的索引k。

• 终止条件：

  1. 返回false：（1）行或列索引越界；or（2）当前矩阵元素与目标字符不同；or（3）当前矩阵元素已访问过（（3）可合并至（2））。
  2. 返回true：k = len(word) - 1，即字符串word已全部匹配。

• 递推工作：

  1. 标记当前矩阵元素：将board[i][j]修改为空字符，代表此元素已访问过，防止之后搜索时重复访问。
  2. 搜索下一单元格：朝当前元素的上、下、左、右四个方向开启下层递归，使用或连接（代表只需找到一条可行路径就直接返回，不再做后续DFS），并记录结果至res。
  3. 还原当前矩阵元素：将board[i][j]元素还原至初始值，即word[k]。

• **返回值：**返回布尔量res，代表是否搜索到目标字符串。

使用空字符（Python: ‘’ , Java/C++: ‘\0’ ）做标记是为了防止标记字符与矩阵原有字符重复。当存在重复时，此算法会将矩阵原有字符认作标记字符，从而出现错误。

复杂度分析：

M,N 分别为矩阵行列大小， KK 为字符串 word 长度。

• 时间复杂度$O(3^{K}MN)$：最差情况下，需要遍历矩阵中长度为K字符串的所有方案，时间复杂度为$O(3^K)$;矩阵中共有MN个起点，时间复杂度为$O(MN)$。
  • 方案数计算：设字符串长度为K，搜索中每个字符有上、下、左、右四个方向可以选择，舍弃回头（上个字符）的方向，剩下3种选择，因此方案数的复杂度为$O(3^K)$。
• 空间复杂度$O(K)$：搜索过程中的递归深度不超过K，因此系统因函数调用累计使用的栈空间占用$O(K)$（因为函数返回后，系统调用的栈空间会释放）。最坏情况下K = MN，递归深度为MN，此时系统栈使用O(MN)的额外空间。

//C++:
class Solution {
public:
    bool exist(vector>& board, string word) {
        rows = board.size();
        cols = board[0].size();
        for(int i = 0; i < rows; i++) {
            for(int j = 0; j < cols; j++) {
                if(dfs(board, word, i, j, 0)) return true;
            }
        }
        return false;
    }
private:
    int rows, cols;
    bool dfs(vector>& board, string word, int i, int j, int k) {
        if(i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k]) return false;
        if(k == word.size() - 1) return true;
        board[i][j] = '\0';
        bool res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || 
                      dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
        board[i][j] = word[k];
        return res;
    }
};

#python:
class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        def dfs(i, j, k):
            if not 0 <= i < len(board) or not 0 <= j < len(board[0]) or board[i][j] != word[k]: return False
            if k == len(word) - 1: return True
            board[i][j] = ''
            res = dfs(i + 1, j, k + 1) or dfs(i - 1, j, k + 1) or dfs(i, j + 1, k + 1) or dfs(i, j - 1, k + 1)
            board[i][j] = word[k]
            return res

        for i in range(len(board)):
            for j in range(len(board[0])):
                if dfs(i, j, 0): return True
        return False

剑指Offer 13 - 机器人的运动范围

解题思路：

本题与矩阵中的路径类似，时典型的搜索&回溯问题。在介绍回溯算法前，为提升计算效率，需要先了解两项前置工作：数位之和计算、可达解分析。——自行百度

方法一：深度优先遍历DFS

• 深度优先搜索：可以理解为暴力法模拟机器人在矩阵中的所有路径。DFS通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
• 剪枝：在搜索中，遇到数位和超出目标值、此元素已访问，则应立即返回，称之为可行性剪枝。

算法解析：

• **递归参数：**当前元素在矩阵中的行列索引$i$和$j$，两者的数位和$si$，$sj$。

• **终止条件：**当(1)行列索引越界 or (2)数位和超过目标值k or (3)当前元素已访问过时，返回0，代表不计入可达解。

• 递推工作：

  1. 标记当前单元格：将索引(i, j)存入Set visited中，代表此单元格已被访问过。
  2. 搜索下一单元格：计算当前元素的下、右两个方向元素的数位和，并开启下层递归。

• **回溯返回值：**返回1 + 右方搜索的可达解总数 + 下方搜索的可达解总数，代表从本单元格递归搜索的可达解总数。

复杂度分析：

​ 设矩阵行列数分别为M, N。

• 时间复杂度O(MN)：最差情况下，机器人遍历矩阵所有单元格，此时时间复杂度为O(MN)。
• 空间复杂度O(MN)：最差情况下，Set visited内存储矩阵所有单元格的索引，使用O(MN)的额外空间。

//C++
class Solution{
public:
    int movingCount(int m, int n, int k){
        vector> visited(m, vector(n, 0)); // MN矩阵初始化，每个元素默认为0
        return dfs(0, 0, 0, 0, visited, m, n, k);
    }
private:
    int dfs(int i, int j, int si, int sj, vector>& visited, int m, int n, int k){
        if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
        visited[i][j] = true;
        return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj, visited, m, n, k) +
                   dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8, visited, m, n, k);
    }
};

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        def dfs(i, j, si, sj):
            if i >= m or j >= n or k < si + sj or (i, j) in visited: return 0
            visited.add((i,j))
            return 1 + dfs(i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj) + dfs(i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8)

        visited = set()
        return dfs(0, 0, 0, 0)

方法二：广度优先遍历BFS

• BFS/DFS ： 两者目标都是遍历整个矩阵，不同点在于搜索顺序不同。DFS 是朝一个方向走到底，再回退，以此类推；BFS 则是按照“平推”的方式向前搜索。
• BFS 实现： 通常利用队列实现广度优先遍历。

算法解析：

• 初始化： 将机器人初始点 (0, 0)加入队列 queue ；

• 迭代终止条件： queue 为空。代表已遍历完所有可达解；

• 迭代工作：

  1. 单元格出队： 将队首单元格的 索引、数位和 弹出，作为当前搜索单元格。
  2. 判断是否跳过： 若 ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过 时，执行 continue 。
  3. 标记当前单元格 ：将单元格索引 (i, j) 存入 Set visited 中，代表此单元格 已被访问过 。
  4. 单元格入队： 将当前元素的 下方、右方 单元格的 索引、数位和 加入 queue 。

• 返回值： Set visited 的长度 len(visited) ，即可达解的数量。

复杂度分析：与方法一一致。

// C++
class Solution{
public:
    int movingCount(int m, int n, int k){
        vector> visited(m, vector(n, 0));
        int res = 0;	// 统计可达解数量
        queue> que;
        que.push({ 0, 0, 0, 0}); // 初始点(0, 0)的索引和数位和
        while(que.size() > 0){
            vector x = que.front();
            que.pop();
            int i = x[0], j = x[1], si = x[2], sj = x[3];
            if(i >= m || j >= n || k < si + sj || visited[i][j]) continue;
            visited[i][j] = true;
            res++;
            que.push({ i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj});
            que.push({i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8});
        }
        return res;
    }
};

#python
class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        queue, visited, = [(0, 0, 0, 0)], set()
        while queue:
            i, j, si, sj = queue.pop(0)
            if i >= m or j >= n or k < si + sj or (i, j) in visited: continue
            visited.add((i,j))
            queue.append((i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj))
            queue.append((i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8))
        return len(visited)

剑指Offer 26 - 树的子结构

解题思路：

若树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点。因此，判断树 B 是否是树 A 的子结构，需完成以下两步工作：

1. 先序遍历树 A 中的每个节点 $n_A$；（对应函数 isSubStructure(A, B)）
2. 判断树 A 中 以$n_A$ 为根节点的子树是否包含树 B 。（对应函数 recur(A, B)）

算法流程：

名词规定：树A的根节点记作节点A，数B的根节点记作节点B

recur(A, B)函数：

1.终止条件：

1. 当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true；
2. 当节点 A 为空：说明已经越过树 A 的叶节点，即匹配失败，返回 false；
3. 当节点 A 和 B 的值不同：说明匹配失败，返回 false；

2.返回值：

1. 判断 A 和 B 的 左子节点 是否相等，即 recur(A.left, B.left) ；
2. 判断 A 和 B 的 右子节点 是否相等，即 recur(A.right, B.right) ；

isSubStructure(A, B) 函数：

1. **特例处理：**当 树 A 为空 或 树 B 为空 时，直接返回 false；

2. 返回值： 若树 B 是树 A 的子结构，则必满足以下三种情况之一，因此用或 || 连接；

   1. 以 节点 A 为根节点的子树 包含树 B ，对应 recur(A, B)；
   2. 树 B 是 树 A 左子树 的子结构，对应 isSubStructure(A.left, B)；
   3. 树 B 是 树 A 右子树 的子结构，对应 isSubStructure(A.right, B)；

   以上 2. 3. 实质上是在对树 A 做 先序遍历 。

复杂度分析：

• 时间复杂度 O(MN) ： 其中 M, N分别为树 A 和 树 B 的节点数量；先序遍历树 A 占用 O(M)，每次调用 recur(A, B) 判断占用 O(N)。
• 空间复杂度 O(M)： 当树 A 和树 B 都退化为链表时，递归调用深度最大。当 M≤N 时，遍历树 A 与递归判断的总递归深度为 M；当 M>N 时，最差情况为遍历至树 A 的叶节点，此时总递归深度为 M。

//C++:

class Solution{
public:
    bool isSubStructure(TreeNode* A, TreeNode* B){
        return (A != nullptr && B != nullptr) && (recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
    }
private:
    bool recur(TreeNode* A, TreeNode* B){
        if(B == nullptr) return true;
        if(A == nullptr || A->val != B->val) return false;
        return recur(A->left, B->left) && recur(A->right, B->right);
    }
};

#python

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        def recur(A, B):
            if not B: return True
            if not A or A.val != B.val: return False
            return recur(A.left, B.left) and recur(A.right, B.right)
        
        return bool(A and B) and (recur(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B))

剑指Offer 27 - 二叉树的镜像

二叉树镜像定义： 对于二叉树中任意节点 root，设其左 / 右子节点分别为 left, right ；则在二叉树的镜像中的对应 root 节点，其左 / 右子节点分别为 right, left 。

方法一：递归法

• 根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。

1. **终止条件：**当节点 root为空时（即越过叶节点），则返回 null；

2. 递推工作：

   1. 初始化节点tmp，用于暂存root的左子节点；
      2. 开启递归 右子节点 mirrorTree(root.right)，并将返回值作为 root的 左子节点 。
      3. 开启递归 左子节点 mirrorTree(tmp)，并将返回值作为 root的 右子节点 。

3. **返回值：**返回当前节点root。

复杂度分析：

• 时间复杂度O(N): 其中N为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用O(N)时间。
• **空间复杂度O(N): **最差情况下（当二叉树退化为链表），递归时系统需使用O(N)大小的栈空间

// Cpp
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if (root == nullptr) return nullptr;
        TreeNode* tmp = root->left;
        root->left = mirrorTree(root->right);
        root->right = mirrorTree(tmp);
        return root;
    }
};

# python
class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        if not root: return
        root.left, root.right = self.mirrorTree(root.right), self.mirrorTree(root.left)
        return root
    
class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        if not root: return
        tmp = root.left
        root.left = self.mirrorTree(root.right)
        root.right = self.mirrorTree(tmp)
        return root

方法二：辅助栈（或队列）

• 利用栈（或队列）遍历树的所有节点node，并交换每个node的左/右子节点。

算法流程：

1. **特例处理：**当root为空时，直接返回null；

2. **初始化：**栈（或队列），并加入根节点root。

3. **循环交换：**当栈stack为空时跳出：；

   1. 出栈：记为node；
      2. 添加子节点：将node左和右子节点入栈；
      3. 交换：交换node的左/右子节点。

4. **返回值：**返回根节点root。

复杂度分析：

• 时间复杂度O(N): 其中N为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用O(N)时间。
• **空间复杂度O(N): **最差情况下（当为满二叉树时），栈stack最多同时存储N/2个节点，占用O(N)额外空间。

// cpp
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root == nullptr) return nullptr;
        stack stack;
        stack.push(root);
        while(!stack.empty())
        {
            TreeNode* node = stack.top();
            stack.pop();
            if (node->left != nullptr) stack.push(node->left);
            if (node->right != nullptr) stack.push(node->right);
            TreeNode* tmp = node->left;
            node->left = node->right;
            node->right = tmp;
        }
        return root;
    }
};

# python
class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        if not root: return
        stack = [root]
        while stack:
            node = stack.pop()
            if node.left: stack.append(node.left)
            if node.right: stack.append(node.right)
            node.left, node.right = node.right, node.left
        return root

剑指Offer 28 - 对称的二叉树

解题思路：

对称二叉树定义： 对于树中 任意两个对称节点 L 和 R，一定有：

• L.val = R.val ：即此两对称节点值相等；
• L.left.val = R.right.val ：即 L的左子节点 和 R的右子节点对称；
• L.right.val = R.left.val ：即 L的右子节点 和 R的左子节点对称。

根据定义，自上而下递归，判断每对左右节点是否对称，从而判断树是否为对称二叉树。

算法流程：

isSymmetric(root):

• 特例处理：若根节点root为空，则直接返回true。
• 返回值： 即 recur(root.left, root.right) ;

recur(L, R) ：

• 终止条件：
  • 当 L 和 R 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 true ；
  • 当 L 或 R 中只有一个越过叶节点： 此树不对称，因此返回 false；
  • 当节点 L 值 $\ne$ 节点 R 值： 此树不对称，因此返回 false；
• 递推工作：
  • 判断两节点 L.left 和 R.right 是否对称，即 recur(L.left, R.right) ；
  • 判断两节点 L.right 和 R.left 是否对称，即 recur(L.right, R.left) ；
• 返回值： 两对节点都对称时，才是对称树，因此用与逻辑符 && 连接。

//cpp
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        return recur(root->left, root->right);
    }
    bool recur(TreeNode* lhs, TreeNode* rhs){
        if( lhs == nullptr && rhs == nullptr) return true;
        if( lhs == nullptr || rhs == nullptr || lhs->val != rhs->val) return false;
        return recur(lhs->left, rhs->right) && recur(lhs->right, rhs->left); 
    }
};

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def recur(L, R):
            if not L and not R: return True
            if not L or not R or L.val != R.val: return false
            return recur(L.left, R.right) and recur(L.right, R.left)
       	
        return not root or recur(root.left, root.right)

剑指Offer 32 - 从上到下打印二叉树Ⅰ

题目描述：从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

解题思路：

层序遍历，也称为二叉树的广度优先搜索（BFS)。BFS通常借助队列的的先入先出特性来实现。划重点

算法流程：

1. 特例处理： 当树的根节点为空，则直接返回空列表 [] ；
2. 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
3. BFS 循环： 当队列 queue 为空时跳出；
   1. 出队： 队首元素出队，记为 node；
   2. 打印： 将 node.val 添加至列表 tmp 尾部；
   3. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
4. 返回值： 返回打印结果列表 res 即可。

class Solution{
public:
	vector levelOrder(TreeNode* root){
        vector res;
        if(!root) return res;
        TreeNode* que;
        queue que;
        que.push(root);
        while(!que.empty()){
            TreeNode* node = que.front();
            que.pop();
            res.push_back(node->val);
            if(node->left) que.push(node->left);
            if(node->right) que.push(node->right);
        }
        return res;
    }
};

剑指Offer 32 - 从上到下打印二叉树Ⅱ

题目描述：从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

与上一题不同的是本题要求将每层的全部节点打印到一行。

解题思路：

1. 按层打印： 题目要求的二叉树的 从上至下 打印（即按层打印），又称为二叉树的 广度优先搜索（BFS）。BFS 通常借助 队列 的先入先出特性来实现。

2. 每层打印到一行： 将本层全部节点打印到一行，并将下一层全部节点加入队列，以此类推，即可分为多行打印。

   

算法流程：

1. 特例处理： 当根节点为空，则返回空列表 [] ；
2. 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
3. BFS 循环： 当队列 queue 为空时跳出；
   1. 新建一个临时列表 tmp ，用于存储当前层打印结果；
   2. 当前层打印循环： 循环次数为当前层节点数（即队列 queue 长度）；
      1. 出队： 队首元素出队，记为 node；
      2. 打印： 将 node.val 添加至 tmp 尾部；
      3. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
   3. 将当前层结果 tmp 添加入 res 。
4. 返回值：返回打印结果列表 res 即可。

// cpp
class Solution{
public:
    vector> levelOrder(TreeNode* root){
        queue que;
        vector> res;
        int cnt = 0;
        if(root != NULL) que.push(root);
        while(!que.empty()){
            vector tmp;
            for(int i = que.size(); i > 0; --i){
                root = que.front();
                que.pop();
                tmp.push_back(root->val);
                if(root->left != NULL) que.push(root->left);
                if(root->right != NULL) que.push(root->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

# python

class Solution:
    def levelOrder(self, root:TreeNode)-> List[List[int]]:
        if not root: return []
        res, queue = [], collections.deque()
        queue.append(root)
        while queue:
            tmp = []
            for _ in range(len(queue)):
                node = queue.popleft()
                tmp.append(node.val)
                 if node.left: queue.append(node.left)
                if node.right: queue.append(node.right)
            res.append(tmp)
        return res

剑指Offer 32 - 从上到下打印二叉树Ⅲ

与前两题相比，本题要求打印顺序交替变化：

方法一：层序遍历+双端队列

• 利用双端队列的两端皆可添加元素的特性，设打印列表（双端队列）tmp，并规定：
  • 奇数层 则添加至tmp尾部
  • 偶数层 则添加至tmp头部

算法流程：

1. 特例处理：当树的根节点为空，则直接返回空列表 [] ；
2. 初始化： 打印结果空列表 res ，包含根节点的双端队列 deque ；
3. BFS 循环： 当 deque 为空时跳出；
   1. 新建列表 tmp ，用于临时存储当前层打印结果；
   2. 当前层打印循环： 循环次数为当前层节点数（即 deque 长度）；
      1. 出队： 队首元素出队，记为 node；
      2. 打印： 若为奇数层，将 node.val 添加至 tmp 尾部；否则，添加至 tmp 头部；
      3. 添加子节点： 若 node 的左（右）子节点不为空，则加入 deque ；
   3. 将当前层结果 tmp 转化为 list 并添加入 res ；
4. 返回值： 返回打印结果列表 res 即可；

class Solution:
    def levelOrder(self, root: TreeNode) ->List[List[int]]:
        if not root: return []
        res, deque = [], collections.deque([root])
        while deque:
            tmp = collections.deque()
            for _ in range(len(deque)):
                node = deque.popleft()
                if len(res) % 2 == 0: tmp.append(node.val)
                else: tmp.appendleft(node.val)
                if node.left: deque.append(node.left)
                if node.right: deque.append(node.right)
            res.append(list(tmp))
        return res

方法二：层序遍历 + 双端队列（奇偶层逻辑分离）

• 方法一代码简短、容易实现；但需要判断每个节点的所在层奇偶性，即冗余了N次判断
• 通过将奇偶层逻辑拆分，可以消除冗余的判断

算法流程：

与方法一对比，仅BFS循环不同。

• **BFS循环：**循环打印奇 / 偶数层，当 deque 为空时跳出；
  1. 打印奇数层： 从左向右 打印，先左后右 加入下层节点；
  2. 若 deque 为空，说明向下无偶数层，则跳出；
  3. 打印偶数层： 从右向左 打印，先右后左 加入下层节点；

class Solution{
public:
    vector> levelOrder(TreeNode* root) {
        deque deque;
        vector> res;
        if(root != NULL) deque.push_back(root):
        while(!deque.empty()) {
            // 打印奇数层
            vector tmp;
            for(int i = deque.size(); i > 0; i--){
                // 从左往右打印
                TreeNode* node = deque.front();
                deque.pop_front();
                tmp.push_back(node->val);
                // 先左后右加入下层节点
                if(node->left != NULL) deque.push_back(node->left);
                if(node->right != NULL) deque.push_back(node->right);
            }
            res.push_back(tmp);
            if(deque.empty()) break;	// 若为空则提前跳出
            // 打印偶数层
            tmp.clear();
            for(int i = deque.size(); i > 0; i--){
                // 从右往左打印
                TreeNode* node = deque.back();
                deque.pop_back();
                tmp.push_back(node->val);
                // 从右往左加入下层节点
                if(node->right != NULL) deque.push_front(node->right);
                if(node->left != NULL) deque.push_front(node->left);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

方法三：层序遍历 + 倒序

• 此方法的优点是只用列表即可，无需其他数据结构。
• 偶数层倒序： 若 res 的长度为 奇数 ，说明当前是偶数层，则对 tmp 执行 倒序 操作。

class Solution{
  vector> levelOrder(TreeNode* root){
      queue que;
      vector> res;
      if(root != NULL) que.push(root);
      while(!que.empty()){
          vector tmp;
          for(int i = que.size(); i > 0; i--){
              TreeNode* node = que.front();
              que.pop();
              tmp.push_back(node->val);
              if(node->left != NULL) que.push(node->left);
              if(node->right != NULL) que.push(node->right);
          }
          if(res.sizee() % 2 == 1) reverse(tmp.begin(), tmp.end());
          res.push_back(tmp);
      }
      return res;
  }  
};

剑指Offer 34 - 二叉树中和为某一值的路径

典型的二叉树方案搜索问题，使用回溯法解决，其包含先序遍历 + 路径记录两部分。

• 先序遍历：按照“根、左、右”的顺序，遍历树的所有节点。

• 路径记录“在线序遍历中，记录从根节点到当前节点的路径。当路径满足①根节点到叶节点形成的路径且②各节点值得和等于目标值sum时，将此路径加入结果列表。

  

算法流程：

pathSum(root, sum) 函数：

• 初始化： 结果列表 res ，路径列表 path 。
• 返回值： 返回 res 即可。

recur(root, tar) 函数：

• 递推参数： 当前节点 root ，当前目标值 tar 。
• 终止条件： 若节点 root 为空，则直接返回。
• 递推工作：
  1. 路径更新： 将当前节点值 root.val 加入路径 path 。
  2. 目标值更新： tar = tar - root.val（即目标值 tar 从 sum 减至 00 ）。
  3. 路径记录： 当 ① root 为叶节点 且 ② 路径和等于目标值 ，则将此路径 path 加入 res 。
  4. 先序遍历： 递归左 / 右子节点。
  5. 路径恢复： 向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.pop() 。

复杂度分析：

• 时间复杂度 O(N) ： N为二叉树的节点数，先序遍历需要遍历所有节点。
• **空间复杂度 O(N)：**最差情况下，即树退化为链表时，path 存储所有树节点，使用 O(N)额外空间。

class Solution {
public:
    vector> pathSum(TreeNode* root, int sum) {
        recur(root, sum);
        return res;
    }
private:
    vector> res;
    vector path;
    void recur(TreeNode* root, int tar) {
        if(root == nullptr) return;
        path.push_back(root->val);
        tar -= root->val;
        if(tar == 0 && root->left == nullptr && root->right == nullptr)
            res.push_back(path);
        recur(root->left, tar);
        recur(root->right, tar);
        path.pop_back();
    }
};

def Solution:
    def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]
    	res, path = [], []
        def recur(root, tar):
            if not root: return
            path.append(root.val)
            tar -= root.val
            if tar == 0 and not root.left and not root.right:
                res.appen(list(path))
            recur(root.left, tar)
            recur(root.right, tar)
            path.pop()
        
        recur(root, sum)
        return res
            

剑指Offer 36 - 二叉搜索树与双向链表

解题思路：

本文解法基于性质：二叉搜索树的中序遍历为递增序列。

将二叉搜索树转换成一个“排序的循环双向链表”，其中包含三个要素：

1. **排序链表：**节点应从小到大排序，因此应使用 中序遍历 “从小到大”访问树的节点。

2. 双向链表： 在构建相邻节点的引用关系时，设前驱节点 pre 和当前节点 cur ，不仅应构建 pre.right = cur ，也应构建 cur.left = pre 。

3. 循环链表： 设链表头节点 head 和尾节点 tail ，则应构建 head.left = tail 和 tail.right = head 。

   

   中序遍历 为对二叉树作 “左、根、右” 顺序遍历，递归实现如下：

   // 打印中序遍历
   void dfs(Node* root) {
       if(root == nullptr) return;
       dfs(root->left); // 左
       cout << root->val << endl; // 根
       dfs(root->right); // 右
   }
   

   根据以上分析，考虑使用中序遍历访问树的各节点 cur ；并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向；中序遍历完成后，最后构建头节点和尾节点的引用指向即可。

   算法流程：

   dfs(cur): 递归法中序遍历；

   1. 终止条件：当节点 cur 为空，代表越过叶节点，直接返回；
   2. 递归左子树，即 dfs(cur.left) ；
   3. 构建链表：
      1. 当 pre 为空时： 代表正在访问链表头节点，记为 head ；
      2. 当 pre 不为空时： 修改双向节点引用，即 pre.right = cur ， cur.left = pre ；
      3. 保存 cur ： 更新 pre = cur ，即节点 cur 是后继节点的 pre ；
   4. 递归右子树，即 dfs(cur.left) ；

   treeToDoublyList(root)：

   1. 特例处理： 若节点 root 为空，则直接返回；
   2. 初始化： 空节点 pre ；
   3. 转化为双向链表： 调用 dfs(root) ；
   4. 构建循环链表： 中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可；
   5. 返回值： 返回链表的头节点 head 即可。

   复杂度分析：

   • 时间复杂度 O(N)： N 为二叉树的节点数，中序遍历需要访问所有节点。
   • 空间复杂度 O(N)： 最差情况下，即树退化为链表时，递归深度达到 N，系统使用 O(N) 栈空间。

class Solution{
public:
    Node* treeToDoublyList(Node* root){
        if(root == nullptr) return nullptr;
        dfs(root);
        head->left = pre; // 1.left = 5 
        pre->right = head; // 5.right = 1
        return head; // return 1
    }
private:
    Node *pre, *head;
    void dfs(Node* cur){
        if(cur == nullptr) return; 
        dfs(cur->left); // 4->2->1->null->null->null
        if(pre != nullptr) pre->right = cur; // 1.right = 2 -> 2.right = 3 -> 3->right = 4 -> 4.right = 5
        else head = cur; // head = 1
        cur->left = pre; // 1.left = nullptr -> 2.left = 1 -> 3.left = 2 -> 4.left = 3 -> 5.left = 4
        pre = cur; // pre = 1 -> pre = 2 -> pre = 3 -> pre = 4 -> pre = 5
        dfs(cur->right); // null->3->null->5->null
    }
};

class Solution:
    def treeToDoubleList(self, root: 'Node') -> 'Node':
        def dfs(cur):
            if not cur: return
            dfs(cur.left)
            if self.pre:
                self.pre.right, cur.left = cur, self.pre
            else:
                self.head = cur
            self.pre = cur
            dfs(cur.right)
        
        if not root: return
        self.pre = None
        dfs(root)
        self.head.left, self.pre.right = self.pre, self.head
        return self.head

剑指Offer 38 - 字符串的排列

解题思路：

对于一个长度为 nn 的字符串（假设字符互不重复），其排列方案数共有：
$$n\times (n-1)\times (n-2)...\times 2\times 1$$
排列方案的生成：

根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第 1位字符（ n种情况）、再固定第 2位字符（ n-1 种情况）、… 、最后固定第 n 位字符（ 1种情况）。

重复排列方案与剪枝：

当字符串存在重复字符时，排列方案中也存在重复的排列方案。为排除重复方案，需在固定某位字符时，保证 “每种字符只在此位固定一次” ，即遇到重复字符时不交换，直接跳过。从 DFS 角度看，此操作称为 “剪枝” 。

递归解析：

1. 终止条件： 当 x = len(c) - 1 时，代表所有位已固定（最后一位只有 11 种情况），则将当前组合 c 转化为字符串并加入 res，并返回；
2. 递推参数： 当前固定位 x ；
3. 递推工作： 初始化一个 Set ，用于排除重复的字符；将第 x 位字符与 i\in∈[x, len(c)] 字符分别交换，并进入下层递归；
   1. 剪枝： 若 c[i] 在 Set 中，代表其是重复字符，因此“剪枝”；
   2. 将 c[i] 加入 Set ，以便之后遇到重复字符时剪枝；
   3. 固定字符： 将字符 c[i] 和 c[x] 交换，即固定 c[i] 为当前位字符；
   4. 开启下层递归： 调用 dfs(x + 1) ，即开始固定第 x + 1 个字符；
   5. 还原交换： 将字符 c[i] 和 c[x] 交换（还原之前的交换）；

class Solution{
public:
    vector permutation(string s){  			// 'abc'
        dfs(s, 0);
        return res;
    }
private:
    vector res;
    void dfs(string s, int x){ // (s,0)(s,1)(s,2)
        if(x == s.size() - 1){ // s.size=3, 0,1,2
            res.push_back(s); // abc/acb						// 添加排列方案
            return;
        }
        set st; //[a]
        for(int i = x; i < s.size(); i++){	//i,x=0,0;i,x=1,1;i,x=2,1;i,x=3,1;i,x=1,0;i,x=2,0
            if(st.find(s[i]) != st.end()) continue; //st.find('b')('c')	// 重复，因此剪枝
            st.insert(s[i]); // a->b->c
            swap(s[i], s[x]); // a<->a,b<->b,c<->b						// 交换，将s[i]固定在第x位
            dfs(s, x + 1); //dfs(s,1)(s,2)(s,2)							// 开启固定第x + 1位字符
            swap(s[i], s[x]); // b<->b,b<->c,a<->a
        }
    }
};

class Solution:
    c, res = list(s), []
    def dfs(x):
        if x == len(c) - 1:
            res.append(''.join(c))
            return
        dic = set()
        for i in range(x, len(c)):
            if c[i] in dic: continue
            dic.add(c[i])
            c[i], c[x] = c[x], c[i]
            dfs(x + 1)
            c[i], c[x] = c[x], c[i]
    dfs(0)
    return res

剑指Offer 54 - 二叉搜索树的第k大节点

解题思路：

本文解法基于性质：二叉搜索树的中序遍历为递增序列。根据此性质，易得二叉搜索树的 中序遍历倒序 为 递减序列 。

因此，求 “二叉搜索树第 kk 大的节点” 可转化为求 “此树的中序遍历倒序的第 kk 个节点”。

中序遍历 为 “左、根、右” 顺序，递归法代码如下：

// cpp
void dfs(TreeNode* root) {
    if(root == nullptr) return;
    dfs(root->left);
    cout << root->val;
    dfs(root->right);
}

# python打印中序遍历
def dfs(root):
    if not root: return
    dfs(root.left)  # 左
    print(root.val) # 根
    dfs(root.right) # 右

中序遍历的倒序 为 “右、根、左” 顺序，递归法代码如下：

// cpp
void dfs(TreeNode* root) {
    if(root == nullptr) return;
    dfs(root->right);
    cout << root->val;
    dfs(root->left);
}

# 打印中序遍历倒序
def dfs(root):
    if not root: return
    dfs(root.right) # 右
    print(root.val) # 根
    dfs(root.left)  # 左

为求第 k 个节点，需要实现以下三项工作：

1. 递归遍历时计数，统计当前节点的序号；
2. 递归到第 k 个节点时，应记录结果 res；
3. 记录结果后，后续的遍历即失去意义，应提前终止（即返回）；

递归解析：

1. 终止条件： 当节点 root 为空（越过叶节点），则直接返回；
2. 递归右子树： 即 dfs(root.right)；
3. 递推工作：
   1. 提前返回： 若 k = 0，代表已找到目标节点，无需继续遍历，因此直接返回；
   2. 统计序号： 执行 k = k - 1（即从 k减至 0）；
   3. 记录结果： 若 k = 0，代表当前节点为第 k大的节点，因此记录 res = root.val；
4. 递归左子树： 即 dfs(root.left)；

// cpp
class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        //if (root == nullptr) return 0;
        dfs(root);
        sort(res.begin(), res.end(), [](const int& a, const int& b){ return a > b;});
        return res[k-1];
    }
private:
    vector res;
    void dfs(TreeNode* root){
        if (root == nullptr) return;
        res.push_back(root->val);
        dfs(root->left);
        dfs(root->right);
    }
};

class Solution{
public:
    int kthLargest(TreeNode* root, int k){
        this->k = k;
        dfs(root);
        return res;
    }
private:
    int res, k;
    void dfs(TreeNode* root){
        if(root == nullptr) return;
        dfs(root->right);
        if(k == 0) return;
        if(--k == 0) res = root->val;
        dfs(root->left);
    }
};

class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        def dfs(root):
            if not root: return
            dfs(root.right)
            if self.k == 0: return
            self.k -= 1
            if self.k == 0: self.res = root.val
            dfs(root.left)
            
        self.k = k
        dfs(root)
        return self.res

剑指Offer 55 - Ⅰ.二叉树的深度

树的遍历方式总体分为两类：深度优先搜索（DFS）、广度优先搜索（BFS）

• **常见DFS：**先序遍历、中序遍历、后续遍历；
• 常见BFS: 层序遍历（即按层遍历）

求树的深度需要遍历树的所有节点。

方法一：后序遍历（DFS）

• 树的后序遍历/深度优先搜索往往利用递归或栈实现。
• **关键点：**此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 +1。

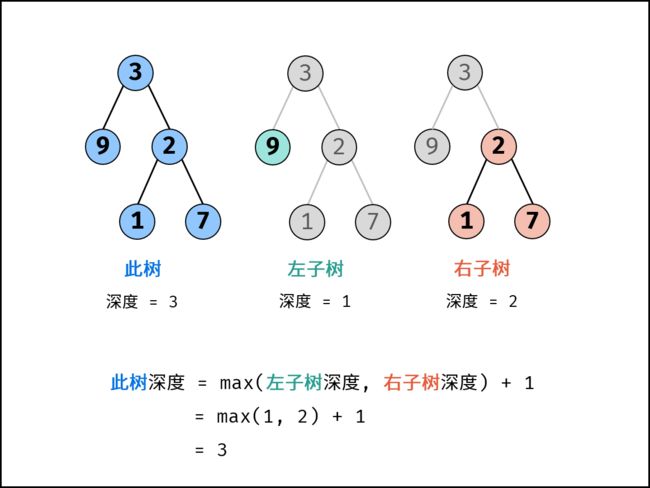
算法解析：

1. 终止条件： 当 root 为空，说明已越过叶节点，因此返回 深度 0。
2. 递推工作： 本质上是对树做后序遍历。
   1. 计算节点 root 的 左子树的深度 ，即调用 maxDepth(root.left)；
   2. 计算节点 root 的 右子树的深度 ，即调用 maxDepth(root.right)；
3. 返回值： 返回 此树的深度 ，即 max(maxDepth(root.left), maxDepth(root.right)) + 1。

• 时间复杂度O(N): N为树的节点数量，计算树的深度需要遍历所有节点。
• 空间复杂度 O(N) ： 最差情况下（当树退化为链表时），递归深度可达到 N。

// cpp
class Solution{
public:
    int maxDepth(TreeNode* root){
        if(root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

# py
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

方法二：层序遍历（BFS）

• 树的层序遍历/广度优先搜索往往使用队列实现
• 关键点： 每遍历一层，则计数器 +1 ，直到遍历完成，则可得到树的深度。

算法解析：

1. 特例处理： 当 root 为空，直接返回 深度 0。
2. 初始化： 队列 queue （加入根节点 root ），计数器 res = 0。
3. 循环遍历： 当 queue 为空时跳出。
   1. 初始化一个空列表 tmp ，用于临时存储下一层节点；
   2. 遍历队列： 遍历 queue 中的各节点 node ，并将其左子节点和右子节点加入 tmp；
   3. 更新队列： 执行 queue = tmp ，将下一层节点赋值给 queue；
   4. 统计层数： 执行 res += 1 ，代表层数加 11；
4. 返回值： 返回 res 即可。

复杂度分析：

• 时间复杂度 O(N) ： N为树的节点数量，计算树的深度需要遍历所有节点。

• 空间复杂度 O(N)： 最差情况下（当树平衡时），队列 queue 同时存储 N/2个节点。

// cpp
class Solution{
public:
    int maxDepth(TreeNode* root){
        if(root == nullptr) return 0;
        vector que;
        que.push_back(root);
        int res = 0;
        while( !que.empty()){
            vector tmp;
            for(auto node : que){
                if(node->left != nullptr) tmp.push_back(node->left);
                if(node->right != nullptr) tmp.push_back(node->right);
            }
            que = tmp;
            res ++;
        }
        return res;
    }
};

# py
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0
        queue, res = [root], 0
        while queue:
            tmp = []
            for node in queue:
                if node.left: tmp.append(node.left)
                if node.right: tmp.append(node.right)
            queue = tmp
            res += 1
        return res

剑指Offer 55 - Ⅱ.平衡二叉树

方法一：后序遍历 + 剪枝 （从底至顶）

思路是对二叉树做后序遍历，从底至顶返回子树深度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。

算法流程：

recur(root) 函数：

• 返回值：

  1. 当节点root 左/右子树的深度差≤1：则返回当前子树的深度，即节点 root 的左/右子树的深度最大值+1（ max(left, right) + 1 ）；
  2. 当节点root 左 / 右子树的深度差>1 ：则返回−1 ，代表 此子树不是平衡树 。

• 终止条件：

  1. 当 root 为空：说明越过叶节点，因此返回高度 0；
  2. 当左（右）子树深度为 -1 ：代表此树的 左（右）子树 不是平衡树，因此剪枝，直接返回 -1；

isBalanced(root) 函数：

• 返回值： 若 recur(root) != -1 ，则说明此树平衡，返回 true； 否则返回 false。

复杂度分析：

• 时间复杂度 O(N)： N 为树的节点数；最差情况下，需要递归遍历树的所有节点。
• 空间复杂度 O(N)： 最差情况下（树退化为链表时），系统递归需要使用 O(N)的栈空间。

class Solution{
public:
    bool isBalanced(TreeNode* root){
        return recur(root) != -1;
    }
private:
    int recur(TreeNode* root){
        if(root == nullptr) return 0; 
        int left = recur(root->left); 
        if(left == -1) return -1;
        int right = recur(root->right);
        if(right == -1) return -1;
        return abs(left - right) < 2 ? max(left, right) + 1 : -1;
    }
};

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def recur(root):
            if not root: return 0
            left = recur(root.left)
            if left == -1:
                return -1
            right = recur(root.right)
            if right == -1:
                return -1
            return max(left, right) + 1 if abs(left - right) <= 1 else -1
        
        return recur(root) != -1

方法二：先序遍历+判断深度（从顶至底）

构造一个获取当前子树的深度的函数 depth(root) ，通过比较某子树的左右子树的深度差 abs(depth(root.left) - depth(root.right)) <= 1是否成立，来判断某子树是否是二叉平衡树。若所有子树都平衡，则此树平衡。

算法流程：

isBalanced(root) 函数： 判断树 root 是否平衡

• 特例处理： 若树根节点 root 为空，则直接返回 true ；
• 返回值： 所有子树都需要满足平衡树性质，因此以下三者使用与逻辑 && 连接；
  1. abs(self.depth(root.left) - self.depth(root.right)) <= 1 ：判断 当前子树 是否是平衡树；
  2. self.isBalanced(root.left) ： 先序遍历递归，判断 当前子树的左子树 是否是平衡树；
  3. self.isBalanced(root.right) ： 先序遍历递归，判断 当前子树的右子树 是否是平衡树；

depth(root) 函数： 计算树 root 的深度

• 终止条件： 当 root 为空，即越过叶子节点，则返回高度 0；
• 返回值： 返回左 / 右子树的深度的最大值 +1。

// cpp
class Solution{
public:
    bool isBalanced(TreeNode* root){
        if(root == nullptr) return true;
        return abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);            
    }
private:
    int depth(TreeNode* root){
        if(root == nullptr) return 0;
        return max(depth(root->left), depth(root->right)) + 1;
    }
};

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root: return True
        return abs(self.depth(root.left) - self.depth(root.right)) <= 1 and \
            self.isBalanced(root.left) and self.isBalanced(root.right)

    def depth(self, root):
        if not root: return 0
        return max(self.depth(root.left), self.depth(root.right)) + 1

复杂度分析：

• 时间复杂度 O(NlogN)： 最差情况下（为 “满二叉树” 时）， isBalanced(root) 遍历树所有节点，判断每个节点的深度 depth(root) 需要遍历各子树的所有节点 。

  • 满二叉树高度的复杂度 O(log N) ，将满二叉树按层分为 log (N+1)层；

  • 通过调用 depth(root) ，判断二叉树各层的节点的对应子树的深度，需遍历节点数量为$ N \times 1, (N-1)/2 \times 2, (N-3)/4 \times 4, …, 1\times (N+1)/2$。因此各层执行 depth(root) 的时间复杂度为 O(N)。

  • 因此，总体时间复杂度 = 每层执行复杂度 × 层数复杂度 = O*(N×log*N) 。

    

• **空间复杂度 O(N)：**最差情况下（树退化为链表时），系统递归需要使用O(N)的栈空间。

剑指Offer 64 - 求1 + 2 + … + n

计算方法主要有三种：平均计算、迭代、递归

方法一：平均计算

问题： 此计算必须使用 乘除法 ，因此本方法不可取，直接排除。

int sumNums(int n){
    return (1 + n) * n / 2;
}

方法二：迭代

问题： 循环必须使用 while 或 for，因此本方法不可取，直接排除。

int sumNums(int n) {
    int res = 0;
    for(int i = 1; i <= n; i++)
        res += i;
    return res;
}

方法三： 递归
问题： 终止条件需要使用 ifif ，因此本方法不可取。
思考： 除了 if和 switch等判断语句外，是否有其他方法可用来终止递归？

int sumNums(int n){
    if(n == 1) return 1;
    n += sumNums(n - 1);
    return n;
}

解题思路：

利用逻辑运算符的短路效应：

if(A && B)  // 若 A 为 false ，则 B 的判断不会执行（即短路），直接判定 A && B 为 false

if(A || B) // 若 A 为 true ，则 B 的判断不会执行（即短路），直接判定 A || B 为 true

class Solution {
public:
    int sumNums(int n) {
        n > 1 && (n += sumNums(n - 1));
        return n;
    }
};

剑指Offer 68 - 二叉搜索树的最近公共祖先Ⅰ

解题思路：

**祖先的定义：**若节点p在节点root的左(右)子树中，或p = root，则称root是p的祖先。

**最近公共祖先的定义：**设节点 root为节点 p,q的某公共祖先，若其左子节点 root.left 和右子节点 root.right都不是 p,q的公共祖先，则称root是 “最近的公共祖先” 。

根据以上定义，若 root是 p,q的 最近公共祖先 ，则只可能为以下三种情况之一：

1. p 和 q在 root的子树中，且分列 root的 异侧（即分别在左、右子树中）；
2. p=root 且 q 在 root的左或右子树中；
3. q=root 且 p 在 root 的左或右子树中；

本题给定了两个重要条件：① 树为二叉搜索树 ，② 树的所有节点的值都是唯一的。根据以上条件，可方便地判断p,q与 root的子树关系，即：

• 若 root.val < p.val，则 p 在 root右子树 中；
• 若 root.val > p.val，则 p 在 root左子树 中；
• 若 root.val = p.val，则 p 和 root指向 同一节点 ；

方法一：迭代

1. **循环搜索：**当节点root为空时跳出
   1. 当p, q都在root的右子树中，则遍历至root.right;
   2. 否则，当p, q都在root的左子树中，则遍历至root.left;
   3. 否则，说明找到了最近公共祖先，跳出；
2. **返回值：**最近公共祖先root；

复杂度分析：

• 时间复杂度 O(N)： 其中 N 为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为logN（满二叉树），最大为N（退化为链表）。
• 空间复杂度 O(1)： 使用常数大小的额外空间。
• 代码优化：若可保证 p.val < q.val，则在循环中可减少判断条件，提升计算效率。

// cpp
class Solution{
public:
    TreeNode* lowestCommonAncester(TreeNode* root, TreeNode* p, TreeNode*q){
        while( root != nullptr){
            if(p->val > root->val && q->val > root->val)
                root = root->right;
            else if(p->val < root->val && q->val < root->val)
                root = root->left;
            else break;
        }
        return root;
    }
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(p->val > q->val)
            swap(p, q);
        while(root != nullptr) {
            if(root->val < p->val) // p,q 都在 root 的右子树中
                root = root->right; // 遍历至右子节点
            else if(root->val > q->val) // p,q 都在 root 的左子树中
                root = root->left; // 遍历至左子节点
            else break;
        }
        return root;
    }
};

# py
class Solution:
    def lowestCommonAncester(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while root:
            if root.val < p.val and root.val < q.val:
            	root = root.right
            elif root.val > p.val and root.val > q.val: # p,q 都在 root 的左子树中
                root = root.left # 遍历至左子节点
            else: break
        return root
    
class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if p.val > q.val: p, q = q, p # 保证 p.val < q.val
        while root:
            if root.val < p.val: # p,q 都在 root 的右子树中
                root = root.right # 遍历至右子节点
            elif root.val > q.val: # p,q 都在 root 的左子树中
                root = root.left # 遍历至左子节点
            else: break
        return root

方法二：递归

1. 递推工作：
   1. 当p, q都在root的右子树中，则开启递归root.right并返回；
   2. 否则，当p, q都在root的左子树中，则开启递归root.left并返回；
2. **返回值：**最近公共祖先root；

复杂度分析：

• **时间复杂度 O(N) ：**其中 N为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为logN（满二叉树），最大为N（退化为链表）。
• 空间复杂度 O(N) ： 最差情况下，即树退化为链表时，递归深度达到树的层数 N 。

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root->val < p->val && root->val < q->val)
            return lowestCommonAncestor(root->right, p, q);
        if(root->val > p->val && root->val > q->val)
            return lowestCommonAncestor(root->left, p, q);
        return root;
    }
};

剑指Offer 68 - 二叉树的最近公共祖先Ⅱ

考虑通过递归对二叉树进行后序遍历，当遇到节点 p或 q时返回。从底至顶回溯，当节点 p, q 在节点 root 的异侧时，节点 root即为最近公共祖先，则向上返回 root。

递归解析：

1. 终止条件：
   1. 当越过叶节点，则直接返回null；
   2. 当root等于p, q，则直接返回root;
2. 递推工作：
   1. 开启递归左子节点，返回值记为left；
   2. 开启递归右子节点，返回值记为right;
3. **返回值：**根据left和right，课展开为四种情况：
   1. 当left和right同时为空：说明root的左/右子树中都不包含p, q，返回null；
   2. 当left和right同时不为空：说明p, q分列在root的异侧（分别在左/右子树），因此root为最近公共祖先，返回root；
   3. 当left为空，right不为空：p, q都不在root的左子树中，直接返回right。具体可分为两种情况：
      1. p, q其中一个在root的右子树中，此时right指向p（假设为p）；
      2. p, q两节点都在root的右子树中，此时的right指向最近公共祖先节点；
   4. 当left不为空，right为空：与情况3同理。

// cpp
class Solution{
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if(root == nullptr || root == p || root == q) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if(left == nullptr) return right;
        if(right == nullptr) return left;
        return root;
    }
};

// 情况1，2，3，4的展开写法如下
class Solution{
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if(root == nullptr || root == p || root == q) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if(left == nullptr && right == nullptr) return nullptr; // 1
        if(left == nullptr) return right; // 3
        if(right == nullptr) return left; // 4
        return root; // 2  if(left != null and right != null)
    }
};

# py
class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root or root == p or root == q:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if not left: return right
        if not right: return left
        return root

rn lowestCommonAncestor(root->left, p, q);
return root;
}
};

### 剑指Offer 68 - 二叉树的最近公共祖先Ⅱ

考虑通过递归对二叉树进行后序遍历，当遇到节点 p或 q时返回。从底至顶回溯，当节点 p, q 在节点 root 的异侧时，节点 root即为最近公共祖先，则向上返回 root。

递归解析：

1. **终止条件：**
   1. 当越过叶节点，则直接返回null；
   2. 当root等于p, q，则直接返回root;
2. **递推工作：**
   1. 开启递归左子节点，返回值记为left；
   2. 开启递归右子节点，返回值记为right;
3. **返回值：**根据left和right，课展开为四种情况：
   1. 当left和right**同时为空**：说明root的左/右子树中都不包含p, q，返回null；
   2. 当left和right**同时不为空**：说明p, q分列在root的**异侧**（分别在左/右子树），因此root为最近公共祖先，返回root；
   3. 当left**为空**，right**不为空**：p, q都不在root的左子树中，直接返回right。具体可分为两种情况：
      1. p, q其中一个在root的**右子树**中，此时right指向p（假设为p）；
      2. p, q两节点都在root的**右子树**中，此时的right指向**最近公共祖先节点**；
   4. 当left**不为空**，right**为空**：与情况3同理。

```c++
// cpp
class Solution{
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if(root == nullptr || root == p || root == q) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if(left == nullptr) return right;
        if(right == nullptr) return left;
        return root;
    }
};

// 情况1，2，3，4的展开写法如下
class Solution{
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if(root == nullptr || root == p || root == q) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if(left == nullptr && right == nullptr) return nullptr; // 1
        if(left == nullptr) return right; // 3
        if(right == nullptr) return left; // 4
        return root; // 2  if(left != null and right != null)
    }
};

# py
class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root or root == p or root == q:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if not left: return right
        if not right: return left
        return root