【C语言从青铜到荣耀——6】
声明:由于作者水平有限,本文难免有错误和不准确之处,本人也很想知道这些错误,恳望读者批评指正。
【联系方式】[email protected]
【更新记录】2021年4月19日(第一次更新 )
【勘误记录】暂无
文章目录
-
-
- 1.什么是函数递归?
-
-
- 递归的俩个必要条件:
-
- 例题:根据下面递归函数:调用函数Fun(2),返回值是多少
- 例题:按照时序打印一个数
-
- 2.递归溢出
-
-
-
- 例题:
-
-
- 3.(多练几次,重在理解):编写函数不允许创建临时变量,求字符串长度。
- 4.递归与迭代
-
-
-
- 例题1:求n的阶乘
- 例题2:求第n个斐波那契数0、1、1、2、3、5、8、13、21、34
-
-
- 5.汉诺塔问题(假设有24个盘子)
- 6.青蛙跳台阶问题(类似斐波那契数列)
- 7.编写一个函数 reverse_string(char \* string)(递归实现)
- 8.写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和
-
1.什么是函数递归?
程序调用自身的编程技巧称为递归。(核心就是大事化小)
递归的俩个必要条件:
*存在限制条件,当满足这一限制条件时,递归便不再继续。
*每次递归调用之后越来越接近这个限制条件。
例题:根据下面递归函数:调用函数Fun(2),返回值是多少
int Fun(int n)
{
if(n==5)
return 2;
else
return 2*Fun(n+1);
}
分析:
Fun(2)--->返回16
return 2*Fun(3) 2*8=16
|__Fun(3):8
return 2*Fun(4) 2*4=8
|__Fun(4):4
return 2*Fun(5) 2*2=4
|__Fun(5):2
return 2
例题:按照时序打印一个数
void print(unsigned int n)//123
{
if (n > 9)
{
print(n / 10);
}
//else 切记这个else不能加,不是非此即彼的关系!!!
printf("%d ", n % 10);
}
int main()
{
unsigned int num = 0;
scanf("%u", &num);//123
//递归 - 函数自己调用自己
print(num);//print函数可以打印参数部分数字的每一位
return 0;
}
解析图:
解析:
我们以输入123为例,首先进入到print(123 / 10);再进入print(12/ 10);再进入print(1 / 10);因为1<9,1 % 10=1,所以先输出1,再往外12% 10=2输出2,再往外层123% 10=3输出3。
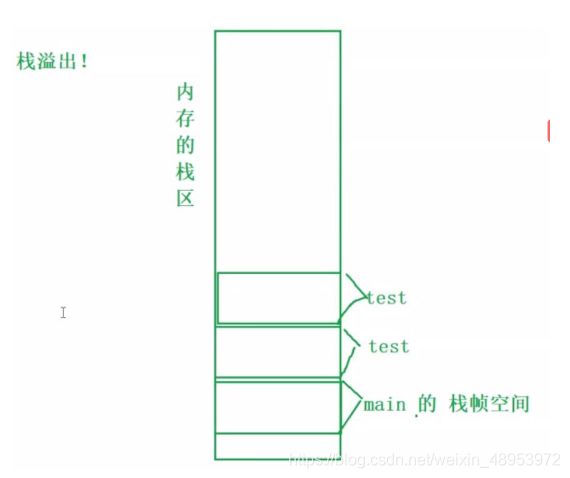
2.递归溢出
例题:
void test(int n)
{
if (n < 10000)//深度递归,容易导致栈溢出
{
test(n + 1);
}
}
int main()
{
int a = 10;
test(1);
return 0;
}
深度递归导致栈溢出!!!
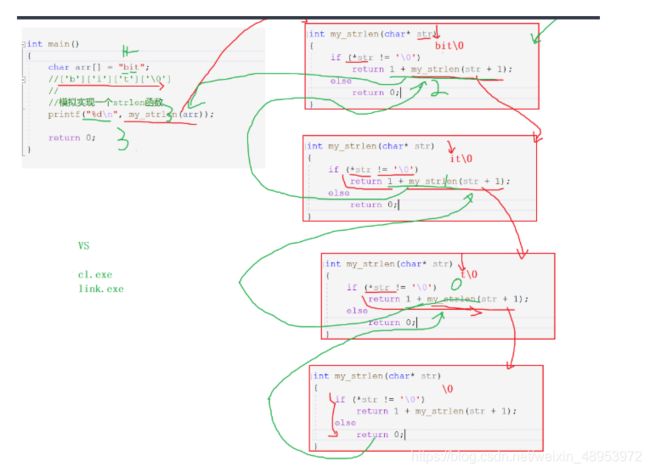
3.(多练几次,重在理解):编写函数不允许创建临时变量,求字符串长度。
#include 解析图:
4.递归与迭代
例题1:求n的阶乘
//1.迭代
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int ret = 1;
for (i = 1; i <= n; i++)
{
ret = ret * i;
}
printf("%d\n", ret);
return 0;
}
//2.递归
int Fac(int n)
{
if (n <= 1)
return 1;
else
return n * Fac(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fac(n);
printf("%d\n", ret);
return 0;
}
//有一些功能:可以使用迭代的方式实现,也可以使用递归
例题2:求第n个斐波那契数0、1、1、2、3、5、8、13、21、34
//递归可以求解,但是效率太低,一直重复计算
//解法1,递归效率极低
int count = 0;
int Fib(int n)
{
//统计第3个斐波那契数的计算机次数
if (n == 3)
count++;
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
printf("count = %d\n", count);
return 0;
}
//解法2,迭代循环
int Fib(int n)
{
int a = 1;
int b = 1;
int c = 1;
while (n>2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}
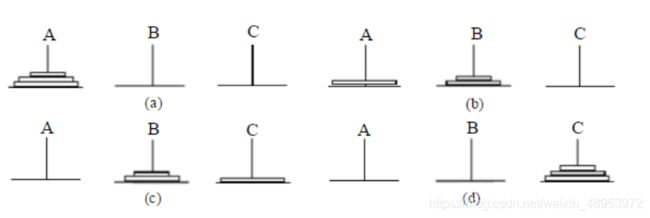
5.汉诺塔问题(假设有24个盘子)
除了a最下面的盘子之外,其他的23个都移动到了b上,这时候把最下面的盘子由a移动到c即可。
当最大的盘子由a移动到c,b上是是剩下的23个盘子。a空了,现在的任务是把23个从b转移到c。
子问题同原问题,只是调整规模24->23。方法类似,先将上面的22个盘子由b移到a,再将最下面的盘子移到c。
…
如此重复递归直到规模达到预定值。
6.青蛙跳台阶问题(类似斐波那契数列)
当n=3时,青蛙最后一次跳的时候有两种可能,一种是最后一次跳了1级,一种是最后一次跳了两级,当n>3时,最后一步跳法同理。
我们将以上思路抽象成数学公式,令f(n)为n级台阶的总跳法数,如果最后一步选择跳1级的话,之前就只有(n-1)级台阶可跳,(n-1)级的总跳法数是f(n-1),如果最后一次跳2级的话,之前就只有(n-2)级台阶可跳,(n-2)级台阶的总跳法数是f(n-2),因为青蛙最后一步不是跳1级就是跳2级,所以刚刚列举的就是青蛙的所有跳法,即f(n)=f(n-1)+f(n-2).
7.编写一个函数 reverse_string(char * string)(递归实现)
实现:将参数字符串中的字符反向排列,不是逆序打印。
**要求:**不能使用C函数库中的字符串操作函数。
/*
非递归思路:
逆置字符串,循环的方式实现非常简单
1. 给两个指针,left放在字符串左侧,right放在最后一个有效字符位置
2. 交换两个指针位置上的字符
3. left指针往后走,right指针往前走,只要两个指针没有相遇,继续2,两个指针相遇后,逆置结束
*/
void reverse_string(char* arr)
{
char *left = arr;
char *right = arr+strlen(arr)-1;
while(left<right)
{
char tmp = *left;
*left = *right;
*right = tmp;
left++;
right--;
}
}
/*
递归方式(好好理解):
对于字符串“abcdefg”,递归实现的大概原理:
1. 交换a和g,
2. 以递归的方式逆置源字符串的剩余部分,剩余部分可以看成一个有效的字符串,再以类似的方式逆置
*/
void reverse_string(char* arr)
{
int len = strlen(arr);
char tmp = *arr;
*arr = *(arr+len-1);
*(arr+len-1) = '\0';
if(strlen(arr+1)>=2)
reverse_string(arr+1);
*(arr+len-1) = tmp;
}
8.写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和
例如,调用DigitSum(1729),则应该返回1+7+2+9,它的和是19
输入:1729,输出:19
/*
思路:
n n < 10
DigiSum(n) =
DibiSum(n/10)+n%10 // 前n-1位之和+第N位
*/
int DigitSum(int n)//1729
{
if(n>9)
return DigitSum(n/10)+n%10;
else
return n;
}