【《机器学习》周志华（西瓜书）】基于信息增益的ID3决策树的构建、可视化及预测的python实现

简介

GitHub地址：https://github.com/One1h/DecisionTree（希望大家可以多多点赞）

本文根据周志华的《机器学习》一书，手写了基于信息增益的ID3决策树的构建，希望大家可以多多提出宝贵意见，共同学习，共同进步！

一、构建决策树-DecisionTree.py

1. 思路

基本算法

基于信息增益的ID3决策树的基本算法

信息熵

“信息熵”（information entropy）是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为Pk（k = 1,2,…,|Y|），则D的信息熵定义为：

Ent(D)的值越小，D的纯度越高。

信息增益

假定离散属性a有V个可能的值a1,a2,…,aV，若使用a来对样本集D进行划分，则会产生V个分支节点，其中第v个分支节点包含了D中所有在属性a上取值为av的样本，记为Dv，这时可以计算出Dv的信息熵，同时考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重|Dv|/|D|，即样本数越多的分支结点的影响越大，于是可计算出用属性a对样本集D进行划分所获得的“信息增益”（information gain）：

一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大。因此，我们可以使用信息增益来进行决策树的划分属性选择。

决策树存储结构

使用了多树来对决策树进行存储，使用列表存储每个节点的子节点，以达到实现动态长度的子节点的树。

2. 代码

import math
from copy import copy
from typing import List
import PlotTree as pt


# 建立数据集
def createDataSet():
    dataSet = [
        # 1
        ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        # 2
        ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        # 3
        ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        # 4
        ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        # 5
        ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        # 6
        ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
        # 7
        ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
        # 8
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],
        # 9
        ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
        # 10
        ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
        # 11
        ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],
        # 12
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
        # 13
        ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
        # 14
        ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
        # 15
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
        # 16
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],
        # 17
        ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']
    ]

    # 特征值列表
    labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']

    # 特征对应的所有可能的情况
    labels_full = {
     }

    for i in range(len(labels)):
        labelList = [example[i] for example in dataSet]
        uniqueLabel = set(labelList)
        labels_full[labels[i]] = uniqueLabel

    return dataSet, labels, labels_full


# 多叉树
class BTreeNode(object):
    def __init__(self, parent=None, keyword=None, child_nodes=[]):
        '''parent：上一层划分属性的具体属性值，如：”浅白“
        keyeyword：此节点的划分属性或label，如：“颜色”
        child_nodes:根据此节点属性的不同属性值划分的子节点集'''
        self.parent = parent
        self.keyword = keyword
        self.child_nodes = child_nodes

    def getkeyword(self):
        return self.keyword

    def addchild(self, node):
        self.child_nodes.append(node)

    def setkeyword(self, keyword):
        self.keyword = keyword

    def setparent(self, parent):
        self.parent = parent

    def shownode(self):
        print("parent:{}\nkeyword:{}\nchild_nodes: ".format(self.parent, self.keyword))
        for node in self.child_nodes:
            print(node.parent, node.keyword)
        print()


# 计算信息熵
def Entropy(pk: float) -> float:
    if pk == 0.0: return 0.0
    return -1 * pk * math.log(pk, 2)


# 计算信息增益
def Gain(D: List[int], Ent: float) -> float:
    G = Ent
    for Dv in D:
        G -= abs(Dv / sum(D)) * Entropy(Dv / sum(D))
    return G


# 获取最佳划分属性
def BestAttribute(dataSet_, labels_, labels_full_):
    # 根节点信息熵计算
    temp = []
    D_t = [0, 0]
    for i, data in enumerate(dataSet_):
        temp.append(i + 1)
        if data[-1] == '好瓜':
            D_t[0] += 1
        if data[-1] == '坏瓜':
            D_t[1] += 1
    Ent = Entropy(D_t[0] / len(temp)) + Entropy(D_t[1] / len(temp))

    # 初始化样本集和信息熵列表
    Gains = []
    for ind, label in enumerate(labels_):
        l = len(labels_full_[label])
        G = Ent
        label_t = list(labels_full_[label])
        D = []
        Ents = []
        for i in range(l):
            D.append([])
            Ents.append(0)

        # 按属性划分Dv
        for i, data in enumerate(dataSet_):
            attribute_ind = label_t.index(data[ind])
            D[attribute_ind].append(i + 1)

        # 计算Dv中各类别数量
        Dv = []
        for i in D:
            temp = [0, 0]
            for j in i:
                if dataSet_[j - 1][-1] == '好瓜':
                    temp[0] += 1
                if dataSet_[j - 1][-1] == '坏瓜':
                    temp[1] += 1
            Dv.append(temp)

        # 计算信息熵
        for i, data in enumerate(Dv):
            good, bad = data
            total = good + bad
            if total != 0:
                Ents[i] = Entropy(good / total) + Entropy(bad / total)

        # 计算信息增益
        for i, data in enumerate(Ents):
            G -= (Dv[i][0] + Dv[i][1]) / len(dataSet_) * data
        Gains.append(G)

    # 寻找最大信息熵的属性
    label_num = 0
    for i, g in enumerate(Gains):
        if g > Gains[label_num]:
            label_num = i

    return labels_[label_num], Gains[label_num]


# 若全为同一类别，返回此类叶结点
def SameClass(dataset_):
    # 若全为同一类别，返回此类叶结点
    label = ''
    same_class = True
    for i, data in enumerate(dataset_):
        if i == 0:
            continue
        if data[-1] != dataset_[i - 1][-1]:
            same_class = False
            break
    if same_class:
        label = dataset_[0][-1]

    return same_class, label


# 属性为空 或 样本在属性上取值相同
def NoneOrSameattr(dataset_, labels_):
    if labels_ != []:
        for i in range(len(dataset_)-2):
            for j in range(i+1, len(dataset_)-1):
                if dataset_[i][:-1] != dataset_[j][:-1]:
                    return False

    return True


# 返回最多类别
def MostClass(dataset_):
    good, bad = 0, 0
    for data in dataset_:
        if data[-1] == '好瓜':
            good += 1
        if data[-1] == '坏瓜':
            bad += 1
    label = '好瓜' if good >= bad else '坏瓜'

    return label


# 对属性划分后不同子集继续生成分支结点
def GetSubNode(dataset_, labels_, labels_full_, best_attr):
    root = BTreeNode(keyword=best_attr)
    subnodes = []
    ind = labels_.index(best_attr)
    # 根据划分属性的不同属性值，对不同属性值的子集进行子树生成
    for attr in labels_full_[best_attr]:
        subtree = BTreeNode()
        subdataset = []
        for i, data in enumerate(dataset_):
            if data[ind] == attr:
                temp = copy(data)
                temp.pop(ind)
                subdataset.append(temp)

        # 该属性值子集为空，设为样本最多的类别
        if not subdataset:
            label = MostClass(dataset_)
            subtree.setkeyword(label)

        # 该属性值子集不为空，继续进行子决策树生成
        else:
            sublabels_full = copy(labels_full_)
            if best_attr in sublabels_full:
                sublabels_full.pop(best_attr)

            sublabels = copy(labels_)
            if best_attr in sublabels:
                sublabels.remove(best_attr)

            subtree = TreeGenerate(subdataset, sublabels, sublabels_full)

        subtree.setparent(attr)
        subnodes.append(subtree)

    return subnodes


# 生成决策树
def TreeGenerate(dataset_, labels_, labels_full_):
    root = BTreeNode()
    # 若全为同一类别，返回此类叶结点
    flag, label = SameClass(dataset_)
    if flag:
        root.setkeyword(label)
        return root

    # 属性为空 或 样本在属性上取值相同，返回最多类别
    if NoneOrSameattr(dataset_, labels_):
        label = MostClass(dataset_)
        root.setkeyword(label)
        return root

    # 选择最优划分属性
    best_attr, gain = BestAttribute(dataset_, labels_, labels_full_)
    root.setkeyword(best_attr)

    # 对属性划分后不同子集继续生成分支结点
    root.child_nodes = GetSubNode(dataset_, labels_, labels_full_, best_attr)
    return root


# 决策树预测
def test(data, dataset, label, labels_full, tree):
    res = ''
    # 遍历决策树，直到得到label
    while res not in ['坏瓜', '好瓜']:
        # 获取划分属性
        attr_divide = tree.keyword
        ind = label.index(attr_divide)

        for node in tree.child_nodes:
            #根据属性值进行划分
            if node.parent == data[ind]:
                tree = node
                res = node.keyword
                break

    return res



if __name__ == '__main__':
    dataSet, labels, labels_full = createDataSet()
    tree = TreeGenerate(dataSet, labels, labels_full)
    pt.createPlot(tree)
    data = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜']
    print(test(data, dataSet, labels, labels_full, tree))

二、决策树可视化-PlotTree.py

1. 思路

使用matplotlib绘制树状图

2. 代码

import matplotlib.pyplot as plt

# 定义matplotlib的字体
plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback']
# boxstyle为文本框的类型，sawtooth是锯齿形，fc是边框线粗细,也可写作 decisionNode={boxstyle:'sawtooth',fc:'0.8'}
decisionNode = dict(boxstyle="round", fc="0.8")
# 定义决策树的叶子结点的描述属性
leafNode = dict(boxstyle="circle", fc="0.8")
# 定义决策树的箭头属性
arrow_args = dict(arrowstyle="<-")


# nodeTxt为要显示的文本，centerPt为文本的中心点，箭头所在的点，parentPt为指向文本的点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="bottom", ha="center",
                            bbox=nodeType, arrowprops=arrow_args)


# 获取叶节点的数目
def getNumLeafs(myTree):
    # 定义叶子结点数目
    numLeaf = 0
    # 得到根据第一个特征分类的结果
    nodes = myTree.child_nodes
    # 遍历得到的子节点
    for node in nodes:
        # 如果node为一个决策树结点，非子节点
        if node.child_nodes:
            # 则递归的计算nodes中的叶子结点数，并加到numLeafs上
            numLeaf += getNumLeafs(node)
        else:
            numLeaf += 1
    # 返回求的叶子结点数目
    return numLeaf


# 获取树的层数
def getTreeDepth(myTree):
    # 定义树的深度
    maxDepth = 0
    # 得到第一个特征分类的结果
    nodes = myTree.child_nodes
    for node in nodes:
        # 如果node为一个决策树结点
        if node.child_nodes:
            thisDepth = 1 + getTreeDepth(node)
        # 如果node为一个决策树结点，非子节点
        else:
            # 则将当前树的深度设为1
            thisDepth = 1
        # 比较当前树的深度与最大数的深度
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    # 返回树的深度
    return maxDepth


# 绘制中间文本
def plotMidText(cntrPt, parentPt, txtString):
    # 求中间点的横坐标
    xMid = (parentPt[0] - cntrPt[0]) / 2.5 + cntrPt[0]
    # 求中间点的纵坐标
    yMid = (parentPt[1] - cntrPt[1]) / 2.5 + cntrPt[1]
    # 绘制树结点
    createPlot.ax1.text(xMid, yMid, txtString)


# 绘制决策树
def plotTree(myTree, parentPt, nodeTxt):
    # 定义并获得决策树的叶子结点数
    numLeafs = getNumLeafs(myTree)
    # 得到第一个特征
    firstStr = myTree.keyword
    # 计算坐标，x坐标为当前树的叶子结点数目除以整个树的叶子结点数再除以3，y为起点
    cntrPt = (plotTree.xOff + (1.0 + numLeafs) / len(myTree.child_nodes) / plotTree.totalW, plotTree.yOff)
    # 绘制决策树结点，也是当前树的根结点
    if parentPt == (0, 0):
        parentPt = cntrPt
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    # 根据第一个特征找到子节点
    nodes = myTree.child_nodes
    # 因为进入了下一层，所以y的坐标要变 ，图像坐标是从左上角为原点
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    # 遍历字节带你
    for node in nodes:
        # 如果node为一棵子决策树，非叶子节点
        if node.child_nodes:
            # 递归的绘制决策树
            plotTree(node, cntrPt, node.parent)
        # node为叶子结点
        else:
            # 计算叶子结点的横坐标
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            # 绘制叶子结点
            plotNode(node.keyword, (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 特征值
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, node.parent)
    # 计算纵坐标
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


# 主函数 绘图
def createPlot(inTree):
    # 定义一块画布
    fig = plt.figure(1, facecolor='white')
    # 清空画布
    fig.clf()
    # 定义横纵坐标轴，无内容
    axprops = dict(xticks=[], yticks=[])
    # 绘制图像，无边框，无坐标轴
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # plotTree.totalW保存的是树的宽
    plotTree.totalW = float(getNumLeafs(inTree))
    # plotTree.totalD保存的是树的高
    plotTree.totalD = float(getTreeDepth(inTree))
    # 决策树起始横坐标
    plotTree.xOff = -0.5 / plotTree.totalW
    # 决策树的起始纵坐标
    plotTree.yOff = 1.0
    # 绘制决策树
    plotTree(inTree, (0, 0), '')
    # 显示图像
    plt.savefig('tree.jpg')

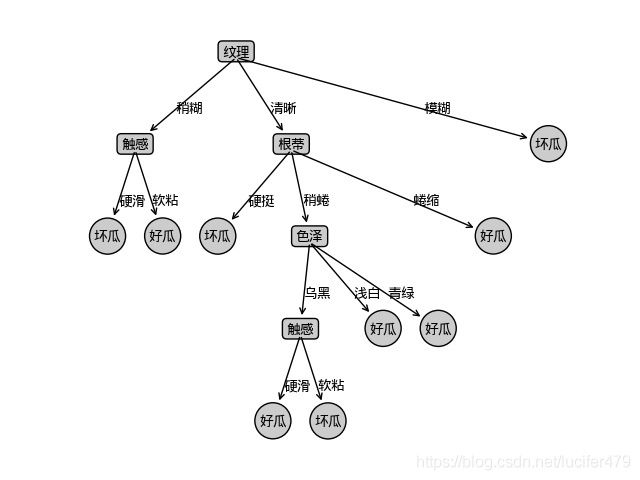
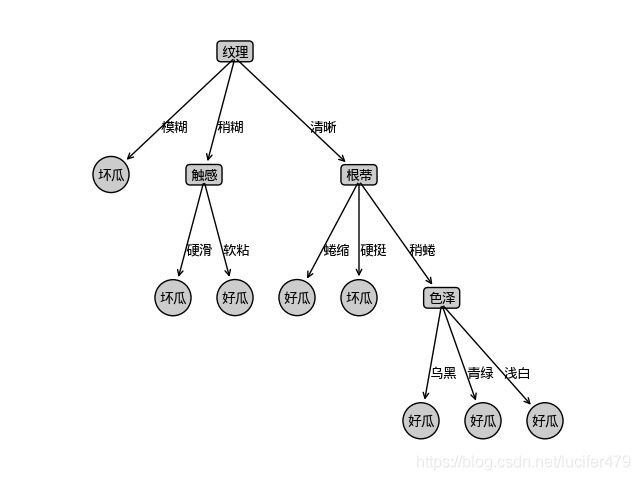
3. 可视化结果

总结

决策树的知识点还不止这些，在此基础上还可添加：

• 划分属性选择的条件，如增益率、基尼指数等；
• 添加剪枝处理，如预剪枝和后剪枝；
• 连续值处理；
• 缺失值处理。