4 二叉树(Binary-Tree)与经典问题——C++&python刷算法
文章目录
- 1.二叉树相关基础知识
-
- 1.1 基础知识
- 1.2 二叉树的三种遍历方式
-
- 用这三个遍历能干啥?
- 根据前序遍历和中序遍历结果 获得二叉树
- 1.3 特殊二叉树的性质
-
- 完全二叉树
- 计算式和记录式
- 数据结构改变的是我们思考问题的方法
- 满二叉树
- 1.4 关于树结构的深入理解
- 2.学习二叉树的作用
-
- 2.1 学习二叉树的两大作用
-
- 作用一 理解 高级数据结构的基础
- 作用二 练习递归技巧的最佳选择
-
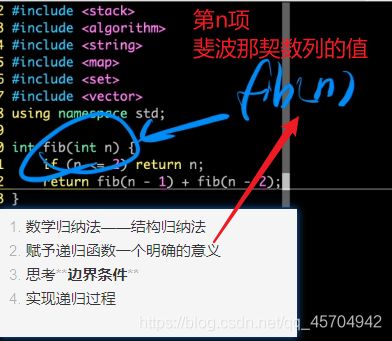
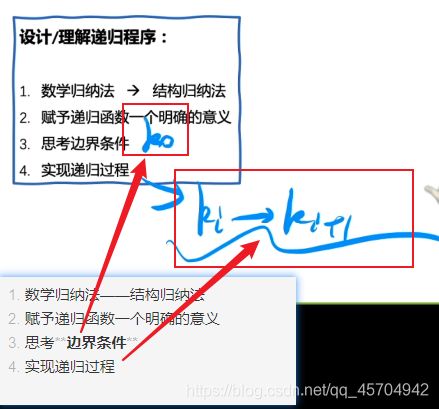
- [重点思想]如何设计/理解递归程序?
- 作用三 左孩子右兄弟表示法节省空间
-
- 为啥转化成二叉树要省空间啊?
- **顺序存储结构和链式存储结构在二叉树上的优劣性
- 3.经典面试题-二叉树的基本操作
-
- 3.1 LC144 二叉树的前序遍历
- 3.2 LC589 N叉树的前序遍历
- 3.3 LC226 翻转二叉树
- 3.4 LC剑指offer32 从上到下打印二叉树II
- 3.5 LC107 二叉树的层序遍历
- 3.6 LC103 二叉树的锯齿形层序遍历
- 4.经典面试题-二叉树的进阶操作
-
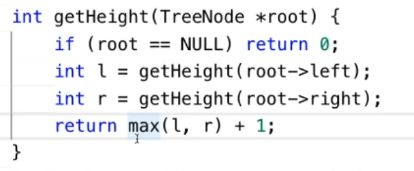
- 4.1 [LC110 平衡二叉树](https://leetcode-cn.com/problems/balanced-binary-tree/)
- 4.2 [LC112 路径总和](https://leetcode-cn.com/problems/path-sum/)
- 4.3 [LC105 从前序和中序遍历序列构造二叉树](https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
- 4.4 [LC222 完全二叉树的节点个数](https://leetcode-cn.com/problems/count-complete-tree-nodes/)
- 4.5 [LC剑指Offer54 二叉搜索树的第k大节点](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/)
- 4.6 [LC剑指 Offer 26. 树的子结构](https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof/)
1.二叉树相关基础知识
1.1 基础知识
基本概念:
证明3——
n节点的树 有n-1条边
所以 节点数 = 边数+1
即为:
n0+n1+n2 (点数)= n1+2*n2+1(边数+1)
=====>n0 = n2 + 1 得证
1.2 二叉树的三种遍历方式
用这三个遍历能干啥?
拿着中序遍历的结果+前序/后序遍历的结果——
可以还原一棵二叉树
【1】先找到根节点
【2】拆出来 左子树中序遍历 左前 右中 右前
【3】再分别还原左子树 右子树
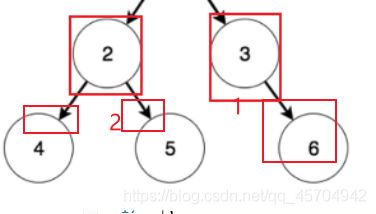
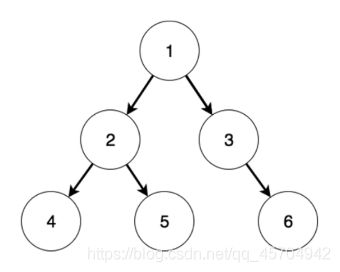
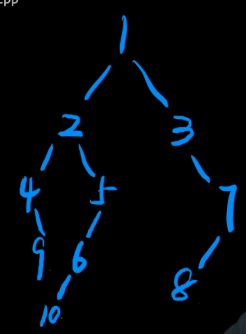
根据前序遍历和中序遍历结果 获得二叉树
前序 1 2 4 9 5 6 10 3 7 8
中序 4 9 2 10 6 5 1 3 8 7
【1】

【2】

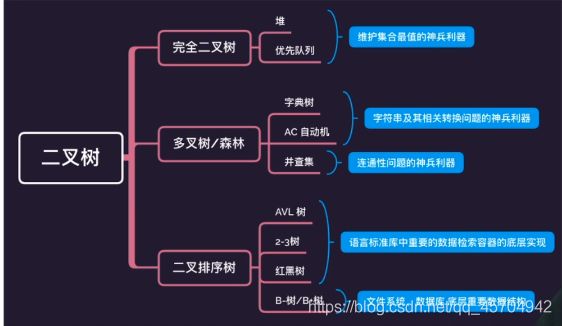
1.3 特殊二叉树的性质
完全二叉树
可以使用连续的空间进行存储(数组)
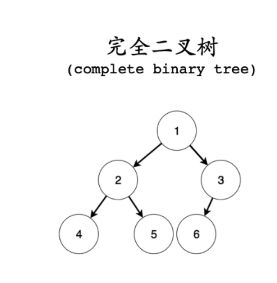
没有度为1的节点,且所有度为0的叶子节点都在同一层
在完全二叉树中不需要记录子树的地址!
节省大量存储空间!!!!!
计算式和记录式
计算式节省空间——时间换空间
“需要节约空间一点的应用”——用计算式!
纪录是节省时间——空间换时间
数据结构改变的是我们思考问题的方法
培养数据结构思维!
满二叉树
没有(出)度为1 的 节点
1.4 关于树结构的深入理解
树的节点——代表集合
边——代表关系
2.学习二叉树的作用
2.1 学习二叉树的两大作用
作用一 理解 高级数据结构的基础
多叉树/森林:
二叉排序树:
- 红黑树 一类非常重要的二叉排序树
- B-(杠)树 B+树:文件系统 数据库 底层重要的数据结构
作用二 练习递归技巧的最佳选择
递归是空间换时间哦~
[重点思想]如何设计/理解递归程序?
作用三 左孩子右兄弟表示法节省空间
为啥转化成二叉树要省空间啊?
举个栗子——
三叉树中每个节点存储3个指针域
有效指针域——指向明确节点的
例如这个三叉树 有63个指针域 其中有效指针域(具体的边)只有5个 浪费了13个指针域
其中k元n叉树中的k和n越大 转换成二叉树越省空间!
n元k叉树浪费的空间——kn -(n-1)
n元2叉树浪费的空间——2n - (n-1)
**顺序存储结构和链式存储结构在二叉树上的优劣性
顺序:比较浪费空间(非完全二叉树时) 进行修改比较困难
读取某个结点的时候效率比较高
链式:空间占用小 容易修改
读取某个指定节点的时候效率偏低O(nlogn)
树形结构基本都是使用链式结构来进行存储
3.经典面试题-二叉树的基本操作
3.1 LC144 二叉树的前序遍历
LC144 二叉树的前序遍历
本人写的解题笔记
class Solution {
public:
void preorder(TreeNode *root,vector<int> &res) {
if (root == NULL) return;
//如果碰到空节点 递归终止
//递归出口是必要的!
res.push_back(root->val); //将根节点值放到结果数组中
//res.push_back(xxx) 在数组res的末尾插入元素xxx
preorder(root->left,res); // 递归左子树
//递归的作用——把遍历到的那个root->val插入res的末尾
preorder(root->right,res); // 递归右子树
return;
}
vector<int>preorderTraversal(TreeNode *root){
// 主函数
vector<int> res; //创建一维数组res
preorder(root, res);//调用写好的前序遍历函数
//两个实参为根节点root 结果数组res从root开始进行遍历
return res;//返回结果数组
}
};
3.2 LC589 N叉树的前序遍历
LC589 N叉树的前序遍历
本人写的解题笔记
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
void __preorder(Node *root,vector<int> &res) {
if (root == NULL) return; //退出条件
res.push_back(root->val); //节点值入队列
for(auto x : root->children)
//迭代容器中所有的元素 每个元素的临时名字为x
__preorder(x,res); //递归遍历
}
}
vector<int> preorder(Node* root) {
vector<int> res;
__preorder(root,res);
return res;
}
};
3.3 LC226 翻转二叉树
LC226 翻转二叉树
本人写的解题笔记
class Solution {
public:
TreeNode* invertTree(TreeNode* root_now) {
if (root_now == NULL) return root_now; //基准条件
swap(root_now->left, root_now->right); //翻转节点
invertTree(root_now->left);
invertTree(root_now->right);
return root_now;
}
};
听这个之后讲的 递归的思路!
3.4 LC剑指offer32 从上到下打印二叉树II
我的解题笔记
LC剑指offer32 从上到下打印二叉树II
本题多了一个递归参数
要记住递归函数的意义是啥?
depth用来标记——代表了现在递归到的层数 每一层都要放到最终的二维结果数组中哦~
class Solution {
public:
void getResult(TreeNode *root, int depth, vector<vector<int>> &ans){
//深度优先搜索
//这个是用于每一层打印结果的函数
if (root == NULL) return;//特例处理
if (depth == ans.size()) {
//在层数与最终结果(二维数组)的长度相同时
ans.push_back(vector<int>());//把当层的数组插入二维数组的末尾!!
}
ans[depth].push_back(root->val);//向结果数组的尾部中加入根节点
getResult(root->left, depth+1, ans);//逐层进行递归
getResult(root->right,depth+1, ans);
return;
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
getResult(root, 0, ans);//从第零层开始遍历
return ans;
}
};
返回双重(二维)数组 刷题笔记 我的刷题笔记 如果不平衡(l<0 || r<0) 返回-2 这题比较偏向数学题 1.找根位置 二叉搜索树的性质:中序遍历得到排列好的序列 *递归——子问题和当前问题 是同一问题
使用vector3.5 LC107 二叉树的层序遍历
LC107 二叉树的层序遍历II
前面这个跟之前一样的~class Solution {
public:
void getResult(TreeNode *root, int depth, vector<vector<int>> &ans){
if (root == NULL){
return;
}
if(depth == ans.size()){
ans.push_back(vector<int>());
}
ans[depth].push_back(root->val);
getResult(root->left, depth+1, ans);
getResult(root->right, depth+1, ans);
return;
}
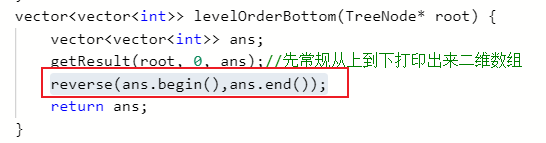
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> ans;
getResult(root, 0, ans);//先常规从上到下打印出来二维数组
reverse(ans.begin(),ans.end());
return ans;
}
};
3.6 LC103 二叉树的锯齿形层序遍历
LC103 二叉树的锯齿形层序遍历class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ans;
if(!root) return ans;
//利用队列实现 BFS按层遍历
queue<TreeNode*> nodeQueue;//定义一个TreeNode*类的队列 nodeQueue(这个解释不太清楚准不准确 是暂时的一个认知)
nodeQueue.push(root);
bool isOrderLeft = true;//记录是否是从左到右插入(true)
while (!nodeQueue.empty()){
//如果队列不为空 就一直循环下去
deque<int> levelList;//定义一个双端队列levelList来存储当层的值
int size = nodeQueue.size();//size存储了当前层值 方便下面对队列进行遍历
for (int i=0; i < size; i++){
//遍历总队列中该层的值并将所有值出队 按标志位存入双端队列 再按固定顺序读取下一层节点值进队列
auto node = nodeQueue.front();//取出队列第一个值 存储到node中
nodeQueue.pop();
if(isOrderLeft) {
//奇数层 从左到右插入双端队列
levelList.emplace_back(node->val);
}
else{
levelList.push_front(node->val);//从容器开头开始插入元素 实现从左往右插入双端队列
}
//接下来读取下一层节点值进入双端队列
if(node->left){
nodeQueue.push(node->left);//左子节点不为空 就插到总队列中
}
if(node->right){
nodeQueue.push(node->right);
}
}
ans.emplace_back(vector<int>{
levelList.begin(),levelList.end()});
//将当前层的值添加到结果数组中
//前面的vector4.经典面试题-二叉树的进阶操作
4.1 LC110 平衡二叉树
平衡 返回数大于等于0

4.2 LC112 路径总和
从根节点到叶子节点 是否有一条路径=所给值
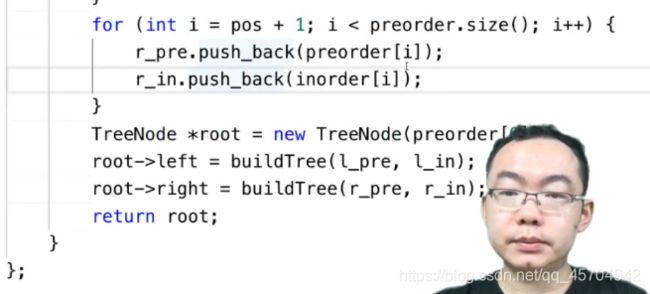
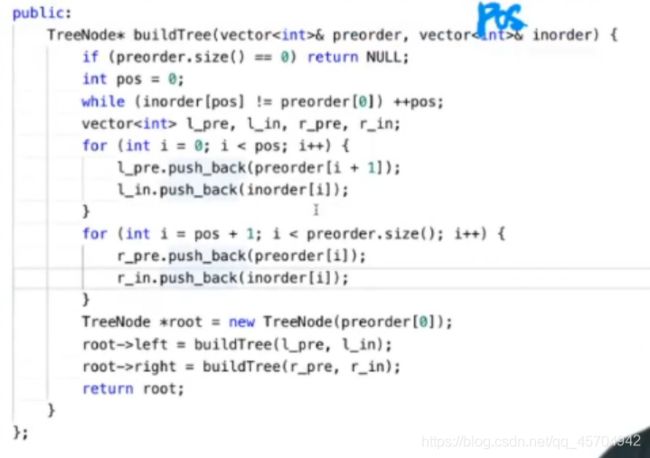
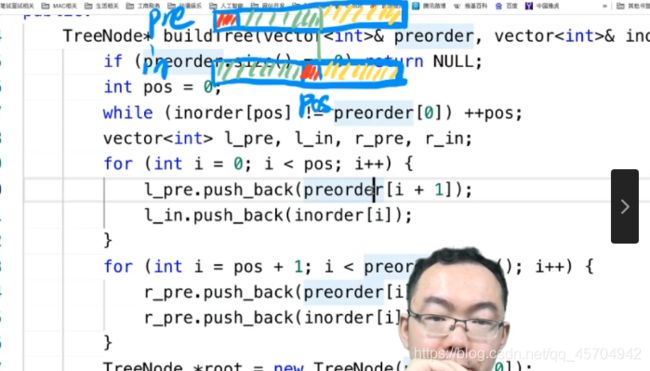
如果左子树不为空 且左子树可以找到一个值=路径值之和4.3 LC105 从前序和中序遍历序列构造二叉树
2.递归建立左 把左子树的前序遍历中序遍历查出来 然后递归建立
3.递归建立右
前序——根左右 中序——左根右

将绿色部分和黄色部分拆出来 ~
4.4 LC222 完全二叉树的节点个数
4.5 LC剑指Offer54 二叉搜索树的第k大节点

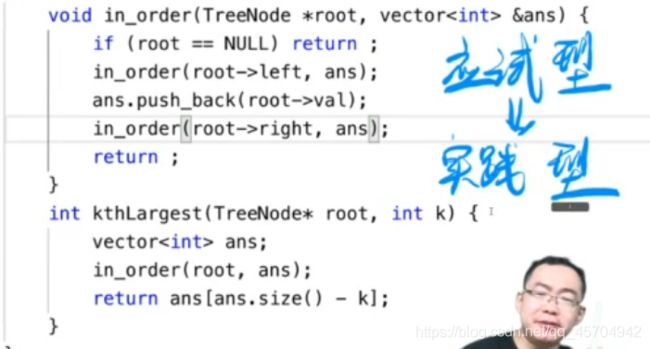
思考 k 和 cnt_r的关系

4.6 LC剑指 Offer 26. 树的子结构