李航老师《统计学习方法》第二版第三章课后题答案
1、参照图3.1,在二维空间中给出实例点,画出 k k k 为1和2时的 k k k 近邻法构成的空间划分,并对其进行比较,体会 k k k 值的选择与模型复杂度及预测准确率的关系。
解:
唉,这一题花了很长时间才搞明白到底是要干啥。下面先简单的介绍一下,到底要干嘛,和k近邻的关系是啥。
我们知道,k近邻算法在对一个新的数据点 A A A 进行分类的时候(这里就以分类来介绍),需要以 A A A为中心,寻找距离 A A A最近的k个点,这k个点是由训练集给出的。然后我们计算这k个点里面,数量最多的类别,作为 A A A的类别,完成分类。该题的意思就是,先根据训练集提前将区域划分好,当有新的数据点 A A A时,我们可以根据 A A A落在哪个区域,从而快速的得出距离点 A A A最近的k个点,下面举个栗子。
栗子: 已知训练集
T = { x 1 , x 2 , . . . , x N } T = \{x_{1},x_{2},...,x_{N}\} T={ x1,x2,...,xN}
设k近邻算法的 k = k 0 k = k_{0} k=k0,在划分区域的时候,假设根据数据 T T T已经划分了下面的 n n n 区域
R = { R 1 , R 2 , . . . , R n } R=\{R_{1}, R_{2},...,R_{n}\} R={ R1,R2,...,Rn}
划分好了区域,其实就是相当于“训练”好了模型,每个子区域 R i R_{i} Ri 都是由 k 0 k_{0} k0个数据点决定的,只不过这个模型只是称为 k 0 k_{0} k0近邻法,对于别的不同的 k k k还要重新划分区域(建立模型)。
假设现在来一个新的点 A A A,我们需要根据 k 0 k_{0} k0近邻判断出数据点 A A A的类别。假设点 A A A落在我们划分的的区域的第 i 0 i_{0} i0个子区域 R i 0 R_{i{0}} Ri0,决定 R i 0 R_{i{0}} Ri0的 k 0 k_{0} k0个点是 x i 01 , x i 02 , . . . , x i 0 k 0 x_{i01},x_{i02},...,x_{i0k_{0}} xi01,xi02,...,xi0k0,那么我们就知道了距离 A A A的最近的 k 0 k_{0} k0个点了,就是 x i 01 , x i 02 , . . . , x i 0 k 0 x_{i01},x_{i02},...,x_{i0k_{0}} xi01,xi02,...,xi0k0,接着我们就可以统计 x i 01 , x i 02 , . . . , x i 0 k 0 x_{i01},x_{i02},...,x_{i0k_{0}} xi01,xi02,...,xi0k0里面的类别数量嘴的类别标签为 A A A的类别。分类完成。
那么问题来了,我们改如何划分区域呢?答案是,使用两点 a , b a,b a,b的垂直平分线,因为垂直平分线上的点距离 a , b a,b a,b的距离相同的。
下面我们开始正式解题:
k 0 = 1 k_{0} = 1 k0=1的栗子:
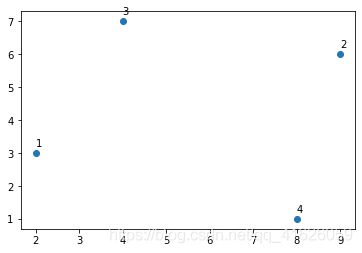
图 1 图1 图1
我们就是要这四个点进行讲解。
接下来,我们依次做点1和4,4和2,2和3,3和1的连线的垂直平分线,并且使得这四条垂直平分线有一些交点。
如下图:
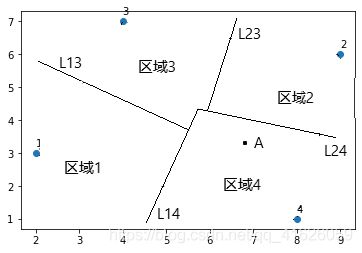
图 2 图2 图2
这样画出垂直平分线之后,使得整个二维平面有了一个区域的划分,其实我们“训练”的k近邻模型,就是对训练数据在高维空间中进行划分。假设上图是我们已经得到的 k = 1 近邻算法模型,现在我们需要对图中的数据点 A A A 进行分类,因为我们在图中使用的都是垂直平分线进行的区域划分,当点 A A A落在数据点2和4的垂直平分线 L 24 L24 L24下侧的时候,相对于点2来说, A A A更加的靠近点4,又因为在点1和4的垂直平分线 L 14 L14 L14的右侧,所以 A A A到点4的距离比到点1的距离更近,所以点 A A A的类别由点4的类别决定,这是因为当 k = 1 k = 1 k=1是模型是最近邻模型。完成分类。
有同学可能会问,为什么没有画出数据点3和4的垂直平分线?这是因为3到1和2的距离比3到4的距离更近,当新的数据点靠近3时,因为点1和2距离3更近,新的数据点可能会到1的距离或者到2的距离比3更近,那么就需要做出23和13的垂直平分线,而不是做出34的垂直平分线。其实画出来也可以,这样更加的规范一些,因为直观上的感觉,为了图省事,我就省略了。所以你明白了吗?
不知道经过上面的讨论之后,你是否对这个区域的划分有了新的理解,如果还是有点懵的话,下面我们在列举一个 k = 2 k = 2 k=2的栗子进行讲解。
k = 2 k = 2 k=2的栗子:此时我们得到的区域划分就是2近邻模型。下面先给出划分之后的图像。首先我们要明白划分的区域的目的是什么,也就是在某个子区域内有一个新的数据点,我们能保证在该子区域内只有两个点距离新的数据点更近,也就是2近邻模型。

图 3 图3 图3
上图3其实就是图2的中几条垂直平分线延长之后相交的得到的结果,我不再对其进严格的分区,我以图3的红色区域为栗子,说一下当一个新的数据点 A A A落在红色区域时,距离 A A A最近的两个点应该是谁。因为点 A A A落在红色区域,点 A A A此时在数据点2和3的垂直平分线L23的右下方,根据垂直平分线的性质,点 A A A到2的距离比到3的距离更近;点 A A A也在数据点1和4的垂直平分线的右下方,因而点 A A A到4的距离比到点1的距离更近,因此,点 A A A的2两个邻近点是点2和4.也就是如果点 A A A落在红色区域,我们根据点2和4的类别对点 A A A进行分类.落在其他的区域也可以这么分析,你明白了没有?
好了,这个题就是这个意思!!!唉,我要吐槽一下,李航老师的书上并没有对这个题进行介绍,直接在后面给了一个习题,需要了解很多额外的知识才行。
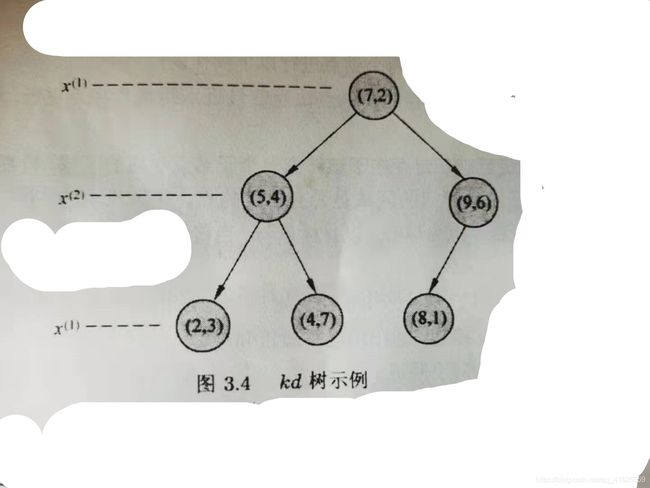
2、利用例题3.2构造的kd树求点(3,4.5)的最近邻点。
我们定位到点(3,4.5)所在叶子节点。这里取距离度量为p=2的欧式距离
因为3<7,所以在根节点(7,2)的左子节点上,又4.5>4,所以在节点的(5,4)的右子节点上,我们先以点(4,7)为点(3,4.5)的当前最近邻点,当前距离为L((4,7),(3,4.5)) = 2.6926
接着向上回退到点(5,4),两点距离为L((5,4),(3,4.5)) = 2.06<2.6926
所以以(5,4)为(3,4.5)的当前最近邻点
下面检查(5,4)的左子节点(2,3)是否比(5,4)更近,因为L((2,3),(3,4.5)) = 1.803 < 2.06,所以(2,3)为(3,4.5)的当前最近邻点,接着继续向上回退到根节点(7,2),显然(7,2)到(3,4.5)的距离更远,我们得到(3,4.5)的最近邻点是(2,3).因为已经退回到根节点,所以搜索结束。最近邻点为(2,3).
3、参照算法3.3,写出输出为x的k近邻算法。
解:大致的想法是维护一个最大堆,就是有k个元素的最大堆,因为堆顶的元素是最大值,因为如果有个点到x的距离小于堆顶元素的值,那么此时需要替换堆顶元素即可。就是有个问题是如果遍历完一个子树之后,这个最大堆没有满,此时就需要继续遍历另外一棵子树。
上面的思路是参考了大神的k近邻算法博客
emmm,但是感觉维护一个有序的栈可能会更好操作一点。