李航老师《统计学习方法》第二版第五章决策树课后答案
1、根据表5.1所给的训练数据集,利用信息增益比(C4.5算法)生成决策树。
解:
下面先给出计算信息增益比的程序,并且输出最好的特征
import numpy as np
def info_ratio(D, Y, n):
'''
计算信息增益比
Parameters
----------
D : numpy array
训练数据集.
Returns
-------
最优特征.
'''
#下面开始修正数据集D和标签Y
for index in n:
s = np.shape(D)
if index == 0:
continue
for i in reversed(range(s[0])):
if D[i,index - 1] == 1:
D = np.delete(D, i, axis = 0)
Y = np.delete(Y, i, axis = 0)
s = np.shape(D)
#下面计算H(D)
#统计类别数
nums_class = len(list(set(Y)))
if nums_class == 1:
print('仅有一个类别,无需在进行分类')
return -2
H_D = 0
#这里时使用自然对数进行计算的
for i in range(nums_class):#i表示类别
nums_i = 0
for j in range(s[0]):
if Y[j] == i:
nums_i += 1
H_D += np.log(nums_i / s[0]) * (nums_i / s[0])
H_D = - H_D
#下面对特征数进行循环
infos_ = []
for A in range(s[1]):
if (A+1) in n:
infos_.append(0)
continue
#循环统计特征A的个数
list_A = list(set(D[:,A]))
nums_A = len(list_A) # 第A个特征的取值范围
H_D_A = 0
H_A_D = 0
for i in range(nums_A):
D_i = sum(np.array(D[:,A] == i, dtype = np.int32))
if D_i != 0:
H_A_D += - (D_i / s[0]) * np.log(D_i / s[0])
for c in range(nums_class):
D_i_k = sum(np.array(D[:, A] == i, dtype = np.int32) * np.array(Y == c, dtype = np.int32))
if D_i_k != 0:
H_D_A += - (D_i / s[0]) * (D_i_k / D_i) * np.log(D_i_k / D_i)
infos_.append((H_D - H_D_A) / H_A_D)
return infos_.index(max(infos_))
if __name__ == '__main__':
D = np.array([[0,0,0,0],
[0,0,0,1],
[0,1,0,1],
[0,1,1,0],
[0,0,0,0],
[1,0,0,0],
[1,0,0,1],
[1,1,1,1],
[1,0,1,2],
[1,0,1,2],
[2,0,1,2],
[2,0,1,1],
[2,1,0,1],
[2,1,0,2],
[2,0,0,0]])
Y = np.array([0,0,1,1,0,0,0,1,1,1,1,1,1,1,0])
n = [0]
for i in range(4):
best = info_ratio(D, Y, n) + 1
if best < 0:
print('构建结束了!!!')
break
print('最优的特征是:', best)
n.append(best)
上面的程序输出是:
最优的特征是: 3
最优的特征是: 2
仅有一个类别,无需在进行分类
构建结束了!!!
第一次的时候,输出的最优的特征是第三个特征:有自己的房子
第二次的时候,输出的最优的特征是第二个特征:有工作
当这两步进行完了的时候,就结束了,因为剩下的数据,只剩下了一个类别的数据,因而无需要再进行分类了。
构造的决策树如下所示:
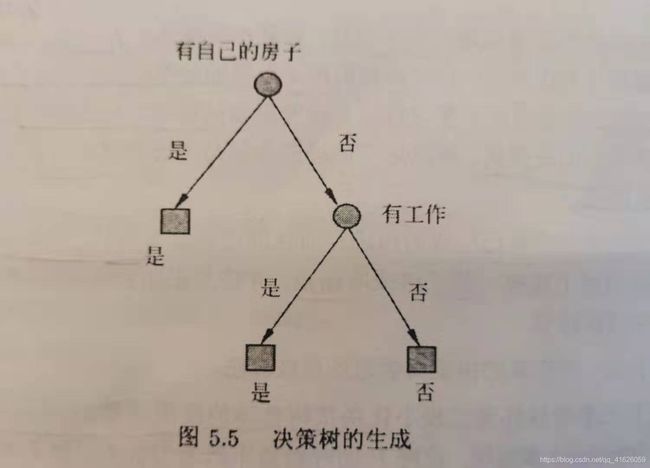
和书上使用ID3算法得到的一样。
2、已知如表5.2所示的训练的数据,试用平方误差损失准则生成一个二叉回归树。
表 5.2 训 练 数 据 表 表5.2 训练数据表 表5.2训练数据表
| x i x_{i} xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y i y_{i} yi | 4.50 | 4.75 | 4.91 | 5.34 | 5.80 | 7.05 | 7.90 | 8.23 | 8.70 | 9.00 |
解:
因为这里面的训练数据的维度只有1,因为计算起来会简单很多,按照书上给的算法,第一次可以计算处使得误差最小的s是5,将数学氛围两部分
D 1 = [ 1 , 2 , 3 , 4 , 5 ] D_{1} = [1,2,3,4,5] D1=[1,2,3,4,5]
D 2 = [ 6 , 7 , 8 , 9 , 10 ] D_{2} = [6,7,8,9,10] D2=[6,7,8,9,10]
Y 1 = Y [ 0 : 5 ] , Y 2 = Y [ 6 : 10 ] Y_{1} = Y[0:5], Y_{2} = Y[6:10] Y1=Y[0:5],Y2=Y[6:10]
然后利用 Y 1 和 Y 2 Y_{1}和Y_{2} Y1和Y2可以分别计算出 c 1 和 c 2 c_{1}和c_{2} c1和c2
然后依次迭代下去
下面给出程序
import numpy as np
class Node:
def __init__(self, s, l_node = None, r_node = None,tag = 'in'):
self.val = s
self.c = 0
self.left_node = l_node
self.right_node = r_node
self.tag = tag
def create_RT(D, Y, Root):
'''
训练数据集和类别标签
Parameters
----------
D : numpy array
数据.
Y : numpy array
标签.
Returns
-------
一棵回归二叉树.
'''
best_s = 0
l = 10*5
for s in D:
Y1 = Y[D <= s]
Y2 = Y[D > s]
c1 = np.mean(Y1)
c2 = np.mean(Y2)
if sum((Y1 - c1) * (Y1 - c1)) + sum((Y2 - c2) * (Y2 - c2)) < l:
l = sum((Y1 - c1) * (Y1 - c1)) + sum((Y2 - c2) * (Y2 - c2))
best_s = s
D1 = D[D <= best_s]
D2 = D[D > best_s]
Y1 = Y[D <= best_s]
Y2 = Y[D > best_s]
Root.val = best_s
Root.c = np.mean(Y)
if len(Y) <= 2:
Root.val = 0
Root.tag = 'leaf'
return
if len(Y1) > 0:
Root.left_node = Node(0)
create_RT(D1, Y1, Root.left_node)
if len(Y2) > 0:
Root.right_node = Node(0)
create_RT(D2, Y2, Root.right_node)
def pre_order(root):
if root == None:
return
if root.tag == 'in':
print('内部节点是:', root.val)
print(root.c)
pre_order(root.left_node)
pre_order(root.right_node)
else:
print('叶子节点:', root.val)
print(root.c)
if __name__ == '__main__':
D = np.array([[1],[2],[3],[4],[5],
[6],[7],[8],[9],[10]]).squeeze()
Y = np.array([4.50, 4.75, 4.91, 5.34, 5.80, 7.05, 7.90, 8.23, 8.70, 9.00])
Root = Node(0)
create_RT(D, Y, Root)
pre_order(Root)
输出是:
内部节点是: 5
对于的均值c是: 6.618
内部节点是: 3
对于的均值c是: 5.0600000000000005
内部节点是: 1
对于的均值c是: 4.72
叶子节点: 0
对应的均值c是: 4.5
叶子节点: 0
对应的均值c是: 4.83
叶子节点: 0
对应的均值c是: 5.57
内部节点是: 7
对于的均值c是: 8.175999999999998
叶子节点: 0
对应的均值c是: 7.475
内部节点是: 8
对于的均值c是: 8.643333333333333
叶子节点: 0
对应的均值c是: 8.23
叶子节点: 0
对应的均值c是: 8.85
因此根据所给的内部节点,可以画出这颗二叉回归树
如下图
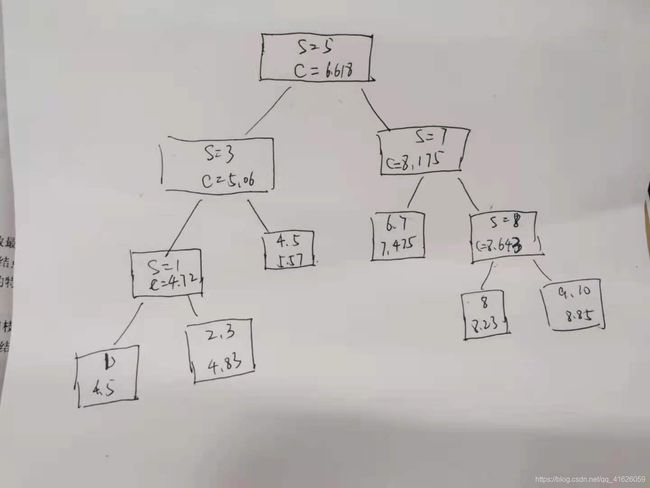
上面每个节点中,如果是内部节点,节点里面第一行的整数代表特征的切分变量的取值,第二行是该节点拟合的数字,也就是书中所说的c,如果是叶子节点,节点内的第一行的数字是代表数据点,第二行是拟合的数值。
总共11个节点,其中6个叶子节点,5个内部节点,我是递归终止条件是当叶子节点里面的数据点的个数小于等于2时停止,也可以设置其他的,因此叶子节点里面的数据个数最多有两个,然后使用他们的均值来逼近需要回归出的那个数。
3、证明CART剪枝算法中,当 α \alpha α确定时,存在唯一的最小子树 T α T_{\alpha} Tα,使损失函数 C α ( T ) C_{\alpha}(T) Cα(T)最小。
证明:
因为从完全生长的决策树的底部剪去一些节点,所形成的二叉树的个数是有限的,因此当 α \alpha α确定的时候,这样的树一定存在。
下面证明唯一性:
假设 T 1 和 T 2 T_{1}和T_{2} T1和T2都使 C α ( T ) C_{\alpha}(T) Cα(T)最小,也就是有 C α ( T 1 ) = C α ( T 2 ) C_{\alpha}(T_{1}) = C_{\alpha}(T_{2}) Cα(T1)=Cα(T2),下面我们证明 T 1 = T 2 T_{1} = T_{2} T1=T2
1、如果两棵树 T 1 和 T 2 T_{1}和T_{2} T1和T2的节点的数量不一样,不如假设树 T 1 T_{1} T1的节点数量更多,因为我们要获得的是可能简单的决策树来减小决策树的过拟合的能力,增大泛化能力,尽管此时两者的损失函数 C α ( T 1 ) = C α ( T 2 ) C_{\alpha}(T_{1}) = C_{\alpha}(T_{2}) Cα(T1)=Cα(T2),但是因为 T 2 T_{2} T2的节点更少,因此此时的最优子树是 T 2 T_{2} T2而不是 T 1 T_{1} T1,因而矛盾。
2、经过上面的讨论,我们知道,如果 T 1 和 T 2 T_{1}和T_{2} T1和T2都是最优的子树的话,那么两者的节点的数量是一样的。对于使用CART算法生成的决策树,对于任何一个节点,要么该节点一个孩子节点也没有,要么一定有两个直系的孩子节点,因为如果节点只有一个孩子节点的话,那么该孩子节点一定可以向上回退到父节点,这和生成算法是矛盾的。至于他们的叶子节点数量我觉得也是一样的。假如 T 1 T_{1} T1的孩子节点比较多,那就说明 T 1 T_{1} T1的深度更深,导致内部节点也更多,此时两者的节点总数是不可能一样的。
假设有下面的树,经过剪枝得到了两个最小的树 T 1 和 T 2 T_{1}和T_{2} T1和T2,他们的叶子节点数量和内部节点数量都是一样的。
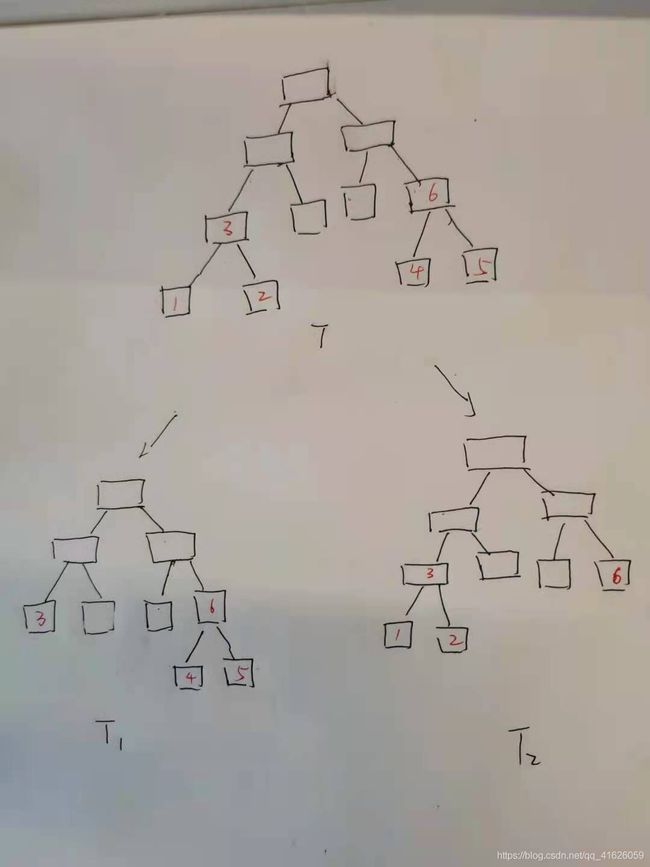
红色的数字为了方便起见,对节点进行的编号。
因为 C α ( T 1 ) = C α ( T 2 ) C_{\alpha}(T_{1}) = C_{\alpha}(T_{2}) Cα(T1)=Cα(T2),由损失函数的定义以及他们的叶子节点数相同,可知, C ( T 1 ) = C ( T 2 ) C(T_{1}) = C(T_{2}) C(T1)=C(T2)
因为树 T T T剪去节点 1 , 2 1,2 1,2得到了 T 1 T_{1} T1,所以 2 α > = C ( 3 ) − C ( 1 ) − C ( 2 ) 2\alpha>=C(3) - C(1)-C(2) 2α>=C(3)−C(1)−C(2),其中 C ( 3 ) C(3) C(3)是节点3内的数据点的损失,比如可以是节点3内数据点的基尼指数或者是平方误差。
那么在决策树 T 2 T_{2} T2中,可以将节点 1 , 2 1,2 1,2剪去得到新的树 T 2 ′ {T_{2}}' T2′,因为 2 α > = C ( 3 ) − C ( 1 ) − C ( 2 ) 2\alpha>=C(3) - C(1)-C(2) 2α>=C(3)−C(1)−C(2),所以,会使得 C α ( T 2 ) > = C α ( T 2 ′ ) C_{\alpha}(T_{2}) >= C_{\alpha}({T_{2}}') Cα(T2)>=Cα(T2′),因而,我们得到一棵更小的决策树。矛盾。得证。
4、证明CART剪枝算法中求出的子树序列 { T 0 , T 1 , . . . , T n } \{T_{0},T_{1},...,T_{n}\} { T0,T1,...,Tn}分别是区间 α ∈ [ α i , α i + 1 ) \alpha \in[\alpha_{i},\alpha_{i+1}) α∈[αi,αi+1)的最优子树 T α T_{\alpha} Tα,这里 i = 0 , 1 , . . . , n , 0 = α 0 < α 1 < . . . . < α n < + ∞ i = 0,1,...,n,0=\alpha_{0}<\alpha_{1}<....<\alpha_{n}<+\infty i=0,1,...,n,0=α0<α1<....<αn<+∞。
证明:
不失一般性,我们只证明 T 1 T_{1} T1是区间 [ α 1 , α 2 ) [\alpha_{1},\alpha_{2}) [α1,α2)内的最优子树就可以,设 ∣ T 0 ∣ |T_{0}| ∣T0∣表示树 T 0 T_{0} T0的叶子节点的个数, t , t 1 , . . . , t ∣ T 0 ∣ − 1 t,t_{1},...,t_{|T_{0}|-1} t,t1,...,t∣T0∣−1表示内部节点, T 0 T_{0} T0剪去 T t T_{t} Tt得到子树 T 1 T_{1} T1
因为
α 1 = C ( t ) − C ( T t ) ∣ T t ∣ − 1 \alpha_{1} =\frac{C(t)-C(T_{t})}{|T_{t}|-1} α1=∣Tt∣−1C(t)−C(Tt)
且有
α 1 < C ( t i ) − C ( T t i ) ∣ T t i ∣ − 1 ; i = 1 , 2 , . . . , ∣ T 0 ∣ − 1 \alpha_{1} < \frac{C(t_{i})-C(T_{t_{i}})}{|T_{t_{i}}|-1};i = 1,2,...,|T_{0}|-1 α1<∣Tti∣−1C(ti)−C(Tti);i=1,2,...,∣T0∣−1
由此我们可以得到
C α 0 ( T 0 ) = C α 1 ( T 1 ) C_{\alpha_0}(T_{0})=C_{\alpha_{1}}(T_{1}) Cα0(T0)=Cα1(T1)
当我们对 T 1 T_{1} T1进行剪枝得到 T 2 T_{2} T2时,因为得到的子树序列是嵌套的,也就是 T 1 T_{1} T1是 T 0 T_{0} T0的子树, T 2 T_{2} T2是 T 1 T_{1} T1的子树等等
因为我们 T 1 T_{1} T1的内部节点我们用 t 11 , t 12 , . . . , t 1 ∣ T 1 ∣ t_{11},t_{12},...,t_{1|T_{1}|} t11,t12,...,t1∣T1∣,因为子树序列的蕴含关系,我们知道集合 { t 11 , t 12 , . . . , t 1 ∣ T 1 ∣ } \{t_{11},t_{12},...,t_{1|T_{1}|}\} { t11,t12,...,t1∣T1∣}是集合 { t 1 , . . . , t ∣ T 0 ∣ − 1 } \{t_{1},...,t_{|T_{0}|-1}\} { t1,...,t∣T0∣−1}的子集。
所以对于任意的 α ′ ∈ [ α 1 , α 2 ) {\alpha}' \in [\alpha_{1},\alpha_{2}) α′∈[α1,α2),均使得下式成立
C α ′ ( T t 1 j ) < C α ′ ( t 1 j ) , j = 1 , . . . , ∣ T 1 ∣ C_{ {\alpha}'}(T_{t_{1j}})
所以上式表明,当 α \alpha α在区间 [ α 1 , α 2 ) [\alpha_{1},\alpha_{2}) [α1,α2)取值时,我们在树 T 1 T_{1} T1上剪去任何子树都会使得新得到子树有比树 T 1 T_{1} T1更大的损失,因此,树 T 1 T_{1} T1是区间 [ α 1 , α 2 ) [\alpha_{1},\alpha_{2}) [α1,α2)内的最优子树。
得证!!!!!!!!!!!!