leetcode周赛-231

5697. 检查二进制字符串字段

AC

题目

给你一个二进制字符串 s ，该字符串 不含前导零 。

如果 s 最多包含 一个由连续的 ‘1’ 组成的字段 ，返回 true​​​ 。否则，返回 false 。

示例 1：

输入：s = "1001"
输出：false
解释：字符串中的 1 没有形成一个连续字段。

示例 2：

输入：s = "110"
输出：true

提示：

1 <= s.length <= 100
s[i]​​​​ 为 '0' 或 '1'
s[0] 为 '1'

解题思路

简单题，从前向后扫，碰到0后停止，检查剩下的字符串里面还有没有1即可

代码

class Solution:
    def checkOnesSegment(self, s: str) -> bool:
        index = 0
        while index < len(s):
            if s[index] == '0':
                break
            index += 1
        return '1' not in s[index:]

5698. 构成特定和需要添加的最少元素

AC

题目

给你一个整数数组 nums ，和两个整数 limit 与 goal 。数组 nums 有一条重要属性：abs(nums[i]) <= limit 。

返回使数组元素总和等于 goal 所需要向数组中添加的 最少元素数量 ，添加元素 不应改变 数组中 abs(nums[i]) <= limit 这一属性。

注意，如果 x >= 0 ，那么 abs(x) 等于 x ；否则，等于 -x 。

示例 1：

输入：nums = [1,-1,1], limit = 3, goal = -4
输出：2
解释：可以将 -2 和 -3 添加到数组中，数组的元素总和变为 1 - 1 + 1 - 2 - 3 = -4 。

示例 2：

输入：nums = [1,-10,9,1], limit = 100, goal = 0
输出：1

提示：

1 <= nums.length <= 10^5
1 <= limit <= 10^6
-limit <= nums[i] <= limit
-10^9 <= goal <= 10^9

解题思路

计算当前数组和与目标之间的差异，然后看看用几个小于等于limit的数能填满即可

代码

class Solution:
    def minElements(self, nums: List[int], limit: int, goal: int) -> int:
        gap = abs(goal - sum(nums))
        return (gap + (limit - 1)) // limit

5699. 从第一个节点出发到最后一个节点的受限路径数

TLE

题目

现有一个加权无向连通图。给你一个正整数 n ，表示图中有 n 个节点，并按从 1 到 n 给节点编号；另给你一个数组 edges ，其中每个 edges[i] = [ui, vi, weighti] 表示存在一条位于节点 ui 和 vi 之间的边，这条边的权重为 weighti 。

从节点 start 出发到节点 end 的路径是一个形如 [z0, z1, z2, …, zk] 的节点序列，满足 z0 = start 、zk = end 且在所有符合 0 <= i <= k-1 的节点 zi 和 zi+1 之间存在一条边。

路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。受限路径 为满足 distanceToLastNode(zi) > distanceToLastNode(zi+1) 的一条路径，其中 0 <= i <= k-1 。

返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大，请返回对 10^9 + 7 取余 的结果。

示例 1：

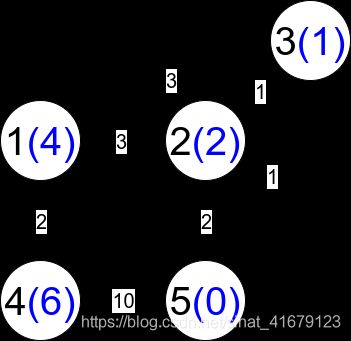
输入：n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
输出：3
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。三条受限路径分别是：
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

示例 2：

输入：n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
输出：1
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。唯一一条受限路径是：1 --> 3 --> 7 。

提示：

1 <= n <= 2 * 10^4
n - 1 <= edges.length <= 4 * 10^4
edges[i].length == 3
1 <= ui, vi <= n
ui != vi
1 <= weight_i <= 10^5
任意两个节点之间至多存在一条边
任意两个节点之间至少存在一条路径

解题思路

建图，然后用BFS算出其他所有节点到节点n的最短路径（即图中蓝色数字）

DFS（TLE）：从1开始DFS，每次往栈里放能走的节点，如果走到n的话，就增加1。注意像例1的情况，节点2会走两遍。这个方法TLE了，我没有分析明白时间复杂度。。。

堆：为了防止例1中节点2走两遍的情况，用堆来DFS。因为每次都是从大的数字向小的数字走，所以每次都挑出当前list中数字最大的节点，把节点可走的邻居都+1，然后不断重复。最后再看n即可

代码

DFS版：

class Solution:
    def countRestrictedPaths(self, n: int, edges: List[List[int]]) -> int:
        # build graph
        graph = {
     }
        for a, b, w in edges:
            if a not in graph:
                graph[a] = []
            graph[a].append((b, w))
            if b not in graph:
                graph[b] = []
            graph[b].append((a, w))
        # bfs for shortest distance
        from collections import deque
        queue = deque([(n, 0)])
        shortest_distance = {
     i: float('inf') for i in range(1, n + 1)}
        while queue:
            node, weight = queue.popleft()          
            if weight < shortest_distance[node]:
                shortest_distance[node] = weight
                for neighbor, n_weight in graph[node]:
                    queue.append((neighbor, weight + n_weight))
        ans = 0
        # dfs
        stack = [(1, shortest_distance[1])]
        while stack:
            node, weight = stack.pop()
            if node == n:
                ans += 1
                continue
            for neighbor, n_weight in graph[node]:
                # if neighbor > node and shortest_distance[neighbor] < weight:
                if shortest_distance[neighbor] < weight:
                    stack.append((neighbor, shortest_distance[neighbor]))
        return ans % (1000000007)

堆版

class Solution:
    def countRestrictedPaths(self, n: int, edges: List[List[int]]) -> int:
        # build graph
        graph = {
     }
        for a, b, w in edges:
            if a not in graph:
                graph[a] = []
            graph[a].append((b, w))
            if b not in graph:
                graph[b] = []
            graph[b].append((a, w))
        # bfs for shortest distance
        from collections import deque
        queue = deque([(n, 0)])
        shortest_distance = {
     i: float('inf') for i in range(1, n + 1)}
        while queue:
            node, weight = queue.popleft()          
            if weight < shortest_distance[node]:
                shortest_distance[node] = weight
                for neighbor, n_weight in graph[node]:
                    queue.append((neighbor, weight + n_weight))
        ans = 0
        import heapq
        dp = {
     i: 0 for i in range(1, n + 1)}
        dp[1] = 1
        heap = [(-shortest_distance[1], 1)]
        visited_nodes = set()
        while heap:
            dis, node = heapq.heappop(heap)
            if node in visited_nodes:
                continue
            visited_nodes.add(node)
            for neighbor, _ in graph[node]:
                if -dis > shortest_distance[neighbor]:
                    dp[neighbor] += dp[node]
                    heapq.heappush(heap, (-shortest_distance[neighbor], neighbor))
        return dp[n] % (1000000007)

5700. 使所有区间的异或结果为零

完全没思路。。。这次好渣

题目

给你一个整数数组 nums​​​ 和一个整数 k​​​​​ 。区间 [left, right]（left <= right）的 异或结果 是对下标位于 left 和 right（包括 left 和 right ）之间所有元素进行 XOR 运算的结果：nums[left] XOR nums[left+1] XOR … XOR nums[right] 。

返回数组中 要更改的最小元素数 ，以使所有长度为 k 的区间异或结果等于零。

示例 1：

输入：nums = [1,2,0,3,0], k = 1
输出：3
解释：将数组 [1,2,0,3,0] 修改为 [0,0,0,0,0]

示例 2：

输入：nums = [3,4,5,2,1,7,3,4,7], k = 3
输出：3
解释：将数组 [3,4,5,2,1,7,3,4,7] 修改为 [3,4,7,3,4,7,3,4,7]

示例 3：

输入：nums = [1,2,4,1,2,5,1,2,6], k = 3
输出：3
解释：将数组[1,2,4,1,2,5,1,2,6] 修改为 [1,2,3,1,2,3,1,2,3]

提示：

1 <= k <= nums.length <= 2000
​​​​​​0 <= nums[i] < ^10