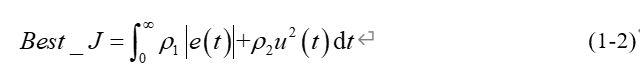【Simulink】NSGA-2优化算法整定PID控制器参数(四)—— 一阶带时延的被控对象
目录
-
- 0研究背景
- 1多目标优化算法的简单介绍
-
- 1.1NSGA-2算法的简单介绍
- 1.3NSGA-2算法的案例实现
- 2被控对象与适应度函数的设计
-
- 2.1被控对象的介绍
- 2.2适应度函数的设计
- 3PID参数整定
-
- 3.1NSGA-2算法的PID参数整定
- 3.3NSGA-2算法的PID参数整定仿真图
- 4参考文献
0研究背景
写在前面:
1.本代码基于MATLAB2019a版本,低版本或者不同版本可能会报错,mdl文件或slx文件打开可能会失败;
2.如果运行时间过长,请观察迭代次数是否有变化。
3.本博客附上代码并详细介绍,如果转载请注明出处;
4.如果本博客恰巧与您的研究有所关联,欢迎您的咨询qq1366196286;
参考博客
【Simulink】PSO优化算法整定PID控制器参数(一)
【Simulink】GA优化算法整定PID控制器参数(三)—— 一阶带时延的被控对象
继续讲解本博客:【Simulink】NSGA-2优化算法整定PID控制器参数(四)—— 一阶带时延的被控对象
1多目标优化算法的简单介绍
基础的概念请参考文献:
[1] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.
[2] Zhang Q, Li H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6):712-731.
1.1NSGA-2算法的简单介绍
NSGA-Ⅱ是目前最流行的多目标遗传算法之一,它降低了非劣排序遗传算法的复杂性,具有运行速度快,解集的收敛性好的优点,成为其他多目标优化算法性能的基准。
NSGA-Ⅱ就是在第一代非支配排序遗传算法的基础上改进而来,其改进主要是针对如上所述的三个方面:
①提出了快速非支配排序算法,一方面降低了计算的复杂度,另一方面它将父代种群跟子代种群进行合并,使得下一代的种群从双倍的空间中进行选取,从而保留了最为优秀的所有个体;
②引进精英策略,保证某些优良的种群个体在进化过程中不会被丢弃,从而提高了优化结果的精度;
③采用拥挤度和拥挤度比较算子,不但克服了NSGA中需要人为指定共享参数的缺陷,而且将其作为种群中个体间的比较标准,使得准Pareto域中的个体能均匀地扩展到整个Pareto域,保证了种群的多样性。
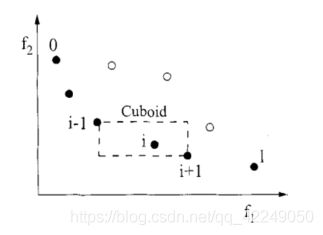
图4-1 拥挤度与拥挤距离的计算
算法目的:
针对当前M个个体,选取N个个体(M>N)。
NSGA-II关键算法(步骤):
1.先对M个个体求pareto解。然后得到F1,F2……等这些pareto的集合。
2.把F1的所有个体全部放入N,若N没满,继续放F2,直到有Fk不能全部放入已经放入F1、F2、…、F(k-1)的N(空间)。此时对Fk进行求解。
3.对于Fk中的个体,求出Fk中的每个个体的拥挤距离Lk[i](crowding distance),在fk中按照Lk[i]递减排序,放入N中,直到N满。

图4-2 NSGA-II的父代与子代产生
其中,NSGA-II关键子程序算法
1)快速非支配排序算法
多目标优化问题的关键在于求取Pareto最优解集。NSGA-II快速非支配排序是依据个体的非劣解水平对种群M进行分层得到Fi,作用是使得解靠近pareto最优解。这是一个循环的适应值分级过程,首先找出群体中的非支配解集,记为F1,将其所有个体赋予非支配序irank=1(其中irank是个体i的非支配序值),并从整个群体M中除去,然后继续找出余下群体中的非支配解集,记为F2,F2中的个体被赋予irank=2,如此进行下去,知道整个种群被分层,Fi层中的非支配序值相同。
2)个体拥挤距离
在同一层Fk中需要进行选择性排序,按照个体拥挤距离(crowding distance)大小排序。个体拥挤距离是Fk上与i相邻的个体i+1和i-1之间的距离,其计算步骤为:
①对同层的个体距离初始化,令L[i]d=0(表示任意个体i的拥挤距离)。
②对同层的个体按照第m个目标函数值升序排列。
③对于处在排序边缘上的个体要给予其选择优势。
④对于排序中间的个体,求拥挤距离:
⑤对于不同的目标函数,重复②到④的步骤,得到个体i的拥挤距离L[i]d,有限选择拥挤距离较大的个体,可以是计算结果在目标空间均匀地分布,维持群体的多样性。
3)精英策略选择算法
保持父代中优良个体直接进入子代,防止Pareto最优解丢失。选择指标对父代Ci和子代Di合成的种群Ri进行优选,组成新父代Ci+1.先淘汰父代中方案检验标志不可行的方案,接着按照非支配序值irank从低到高将整层种群依次放入Ci+1,直到放入某一层Fk超过N的限制,最后,依据拥挤距离大小填充Ci+1直到种群数量为N。
其中,图4-3为双目标函数的Pareto前沿面,其中目标函数f1和f2均是越小越好。实线和虚线组成部分组成为可行域,实线表示pareto前沿面,也就是所有pareto最优解对应的目标矢量组成的曲面,一个多目标优化问题对应一个pareto前沿面。此外,A、B、C三点位于pareto前沿面上,该三点的解为pareto最优解,他们三者之间不存在支配或是占优关系。D、E、F三点的解为可行解,非pareto最优解。A点的解支配F点的解,或是相比F点的解,A点的解是pareto占优。同样B和C点与D、E、F点之间存在支配关系或是占优关系。
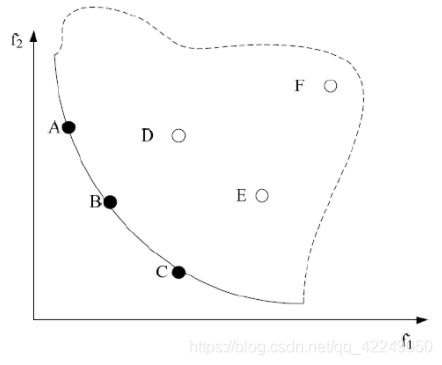
图4-3 双目标函数下非支配解的Pareto前沿面
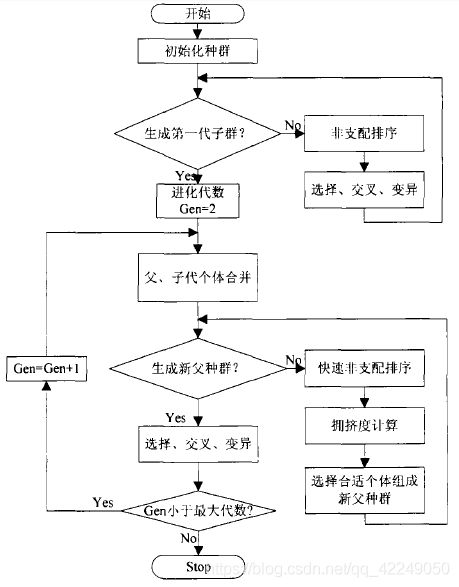
图4-4 NSGA-II算法的一般步骤
NSGA-2算法的伪代码
排序算法的伪代码
def fast_nondominated_sort( P ):
F = [ ]
for p in P:
Sp = [ ]
np = 0
for q in P:
if p > q: # 如果p支配q,把q添加到Sp列表中
Sp.append( q )
else if p < q: # 如果p被q支配,则把np加1
np += 1
if np == 0:
p_rank = 1 # 如果该个体的np为0,则该个体为Pareto第一级
F1.append( p )
F.append( F1 )
i = 0
while F[i]:
Q = [ ]
for p in F[i]:
for q in Sp: # 对所有在Sp集合中的个体进行排序
nq -= 1
if nq == 0: # 如果该个体的支配个数为0,则该个体是非支配个体
q_rank = i + 2 # 该个体Pareto级别为当前最高级别加1。此时i初始值为0,所以要加2
Q.append( q )
F.append( Q )
i += 1
个体拥挤距离算子的伪代码
def crowding_distance_assignment( I )
nLen = len( I ) # I中的个体数量
for i in I:
i.distance = 0 # 初始化所有个体的拥挤距离
for objFun in M: # M为所有目标函数的列表
I = sort( I, objFun ) # 按照目标函数objFun进行升序排序
I[0] = I[ len[I] - 1 ] = ∞ # 对第一个和最后一个个体的距离设为无穷大
for i in xrange( 1 , len(I) - 2 ):
I[i].distance = I[i].distance + ( objFun( I[i + 1 ] ) - objFun( I[i - 1 ] ) ) / (Max(objFun()) - Min(objFun()) )
1.3NSGA-2算法的案例实现
本博客贴上NSGA-Ⅱ算法Matlab实现(测试函数为ZDT1),原文链接:NSGA-Ⅱ算法Matlab实现(测试函数为ZDT1)
代码如下:
function f = evaluate_objective(x, M, V)
f = [];
f(1) = x(1);
g = 1;
sum = 0;
for i = 2:V
sum = sum + x(i);
end
g = g + 9*sum / (V-1));
f(2) = g * (1 - sqrt(x(1) / g));
end
NSGA2代码实现如下:
function NSGAII()
clc;
format compact;
tic;
hold on
%---初始化/参数设定
generations=100; %迭代次数
popnum=100; %种群大小(须为偶数)
poplength=30; %个体长度
minvalue=repmat(zeros(1,poplength),popnum,1); %个体最小值
maxvalue=repmat(ones(1,poplength),popnum,1); %个体最大值
population=rand(popnum,poplength).*(maxvalue-minvalue)+minvalue; %产生新的初始种群
%---开始迭代进化
for gene=1:generations %开始迭代
%-------交叉
newpopulation=zeros(popnum,poplength); %子代种群
for i=1:popnum/2 %交叉产生子代
k=randperm(popnum); %从种群中随机选出两个父母,不采用二进制联赛方法
beta=(-1).^round(rand(1,poplength)).*abs(randn(1,poplength))*1.481; %采用正态分布交叉产生两个子代
newpopulation(i*2-1,:)=(population(k(1),:)+population(k(2),:))/2+beta.*(population(k(1),:)-population(k(2),:))./2; %产生第一个子代
newpopulation(i*2,:)=(population(k(1),:)+population(k(2),:))/2-beta.*(population(k(1),:)-population(k(2),:))./2; %产生第二个子代
end
%-------变异
k=rand(size(newpopulation)); %随机选定要变异的基因位
miu=rand(size(newpopulation)); %采用多项式变异
temp=k<1/poplength & miu<0.5; %要变异的基因位
newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*((2.*miu(temp)+(1-2.*miu(temp)).*(1-(newpopulation(temp)-minvalue(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21)-1); %变异情况一
newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*(1-(2.*(1-miu(temp))+2.*(miu(temp)-0.5).*(1-(maxvalue(temp)-newpopulation(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21)); %变异情况二
%-------越界处理/种群合并
newpopulation(newpopulation>maxvalue)=maxvalue(newpopulation>maxvalue); %子代越上界处理
newpopulation(newpopulation<minvalue)=minvalue(newpopulation<minvalue); %子代越下界处理
newpopulation=[population;newpopulation]; %合并父子种群
%-------计算目标函数值
functionvalue=zeros(size(newpopulation,1),2); %合并后种群的各目标函数值,这里的问题是ZDT1
functionvalue(:,1)=newpopulation(:,1); %计算第一维目标函数值
g=1+9*sum(newpopulation(:,2:poplength),2)./(poplength-1);
functionvalue(:,2)=g.*(1-(newpopulation(:,1)./g).^0.5); %计算第二维目标函数值
%-------非支配排序
fnum=0; %当前分配的前沿面编号
cz=false(1,size(functionvalue,1)); %记录个体是否已被分配编号
frontvalue=zeros(size(cz)); %每个个体的前沿面编号
[functionvalue_sorted,newsite]=sortrows(functionvalue); %对种群按第一维目标值大小进行排序
while ~all(cz) %开始迭代判断每个个体的前沿面,采用改进的deductive sort
fnum=fnum+1;
d=cz;
for i=1:size(functionvalue,1)
if ~d(i)
for j=i+1:size(functionvalue,1)
if ~d(j)
k=1;
for m=2:size(functionvalue,2)
if functionvalue_sorted(i,m)>functionvalue_sorted(j,m)
k=0;
break
end
end
if k
d(j)=true;
end
end
end
frontvalue(newsite(i))=fnum;
cz(i)=true;
end
end
end
%-------计算拥挤距离/选出下一代个体
fnum=0; %当前前沿面
while numel(frontvalue,frontvalue<=fnum+1)<=popnum %判断前多少个面的个体能完全放入下一代种群
fnum=fnum+1;
end
newnum=numel(frontvalue,frontvalue<=fnum); %前fnum个面的个体数
population(1:newnum,:)=newpopulation(frontvalue<=fnum,:); %将前fnum个面的个体复制入下一代
popu=find(frontvalue==fnum+1); %popu记录第fnum+1个面上的个体编号
distancevalue=zeros(size(popu)); %popu各个体的拥挤距离
fmax=max(functionvalue(popu,:),[],1); %popu每维上的最大值
fmin=min(functionvalue(popu,:),[],1); %popu每维上的最小值
for i=1:size(functionvalue,2) %分目标计算每个目标上popu各个体的拥挤距离
[~,newsite]=sortrows(functionvalue(popu,i));
distancevalue(newsite(1))=inf;
distancevalue(newsite(end))=inf;
for j=2:length(popu)-1
distancevalue(newsite(j))=distancevalue(newsite(j))+(functionvalue(popu(newsite(j+1)),i)-functionvalue(popu(newsite(j-1)),i))/(fmax(i)-fmin(i));
end
end
popu=-sortrows(-[distancevalue;popu]')'; %按拥挤距离降序排序第fnum+1个面上的个体
population(newnum+1:popnum,:)=newpopulation(popu(2,1:popnum-newnum),:); %将第fnum+1个面上拥挤距离较大的前popnum-newnum个个体复制入下一代
end
%---程序输出
fprintf('已完成,耗时%4s秒\n',num2str(toc)); %程序最终耗时
output=sortrows(functionvalue(frontvalue==1,:)); %最终结果:种群中非支配解的函数值
plot(output(:,1),output(:,2),'*b'); %作图
axis([0,1,0,1]);xlabel('F_1');ylabel('F_2');title('ZDT1')
end
运行出来的结果图,如下图所示:
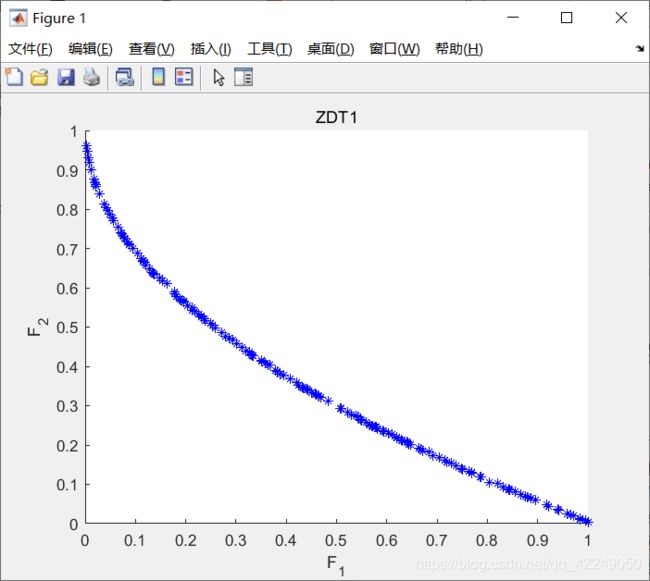
图4-6 NSGA-2算法的案例实现结果图
function y=f(x)
y(1)=x(1)^4-10*x(1)^2+x(1)*x(2)+x(2)^4-x(1)^2*x(2)^2
y(2)=x(2)^4-x(1)^2*x(2)^2+x(1)^4+x(1)*x(2)
NSGA-2 MATLAB自带函数的代码实现如下:
% 目前的多目标优化算法有很多,?Kalyanmoy?Deb的带精英策略的快速非支配排序遗传算法(NSGA-II)
%无疑是其中应用最为广泛也是最为成功的一种。本文用的算法是MATLAB自带的函数gamultiobj,该函数是基于NSGA-II改进的一种多目标优化算法。
clc;
clear all;
fitnessfcn=@object_fun; %适应度函数句柄,目标函数
nvars=2; %变量个数x1 x2
lb=[-5,-5]; %下限
ub=[5,5]; %上限
A=[];
b=[]; %线性不等式约束
Aeq=[];
beq=[]; %线性等式约束
options=gaoptimset('paretoFraction',0.3,'populationsize',500,'generations',200,...
'stallGenLimit',200,'TolFun',1e-100,'PlotFcns',@gaplotpareto);
%最优个体系数paretoFaction为 0.3;种群大小populationsize 为100,
%最大进化代数 generations 为 200 停止代数stallGenlimit为200,
%适应度函数偏差 TolFun 设为1e-100 函数gaplotpareto:绘制Pareto前端
[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options) %MATLAB自带的函数gamultiobj
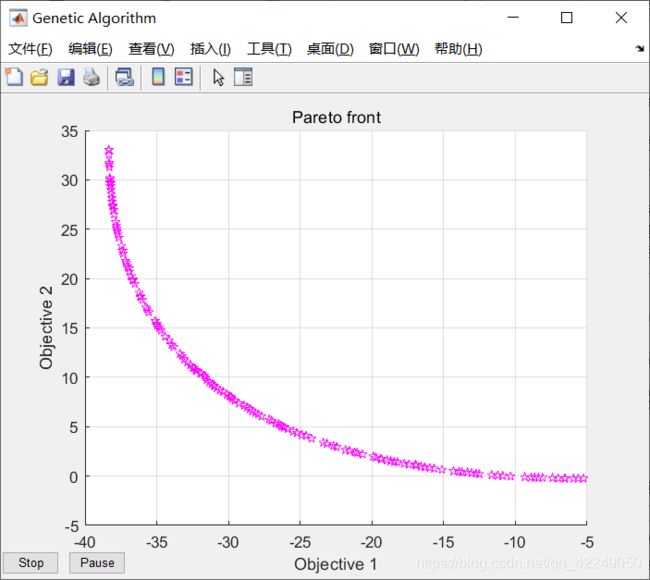
图4-7 NSGA-2 MATLAB自带函数的案例实现结果图
2被控对象与适应度函数的设计
2.1被控对象的介绍
以下式二阶Ⅰ型时延系统的传递函数为例,运用NSGA-2算法进行PID参数优化,其中系统设置为采样时间1 ms,指令为单位阶跃信号,仿真运行时间为1.0 s。其中,性能优化函数Best_J采取时间与误差绝对值乘积的积分方程(Integral of Time Multiplied by the Absolute Value of Error,ITAE),同时为避免控制量过大而产生超调,在性能优化函数Best_J中添加PID控制器输入量的平方项。这仅仅是其中某个目标的适应度函数,此外还需设计另外目标的适应度函数,如2.2适应度函数的设计。
二阶Ⅰ型时延系统的传递函数,如下所示。可按照自己的实际系统进行设计,既可以.m文件进行编写

2.2适应度函数的设计
(1)目标适应度函数1
为获取较为满意的过渡过程,采用误差绝对值时间积分性能指标作为适应度评价函数Best_J。同时为防止控制输入过大,在Best_J加入控制输入的评分项,如式(1-2)所示。
式(1-2)中e(t)为系统输出误差,u(t)为PID控制器输入量,ρ1,ρ2为权重值。
为避免超调,采用罚函数对超调量进行优先处理,则如式(1-3)所示。
![]()
式(1-3)中ρ3>>max(ρ1,ρ2和ρ4),且y(t)为被控对象输出,ey(t)=y(t)-y(t-1)。
此为第一目标适应度函数的设计。
(2)目标适应度函数2
将系统的上升时间、调节时间和延迟时间等响应时间按时间最小性原则进行叠加,构造成第二目标适应度函数的设计。
3PID参数整定
3.1NSGA-2算法的PID参数整定
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global rin yout timef
pop = 500; %种群数量
gen = 100; %迭代次数
M = 2; %目标数量
V = 3; %维度
MinX(1) = 0*ones(1); %Kp
MaxX(1) = 30*ones(1);
MinX(2) = 0*ones(1); %Kp
MaxX(2) = 1.0*ones(1);
MinX(3) = 0*ones(1); %Kp
MaxX(3) = 1.0*ones(1);
min_range = [MinX(1) MinX(2) MinX(3)]; %下界
max_range = [MaxX(1) MaxX(2) MaxX(3)]; %上界
%% 初始化
chromosome = initialize_variables(pop, M, V, min_range, max_range);
%对初始化种群进行非支配快速排序和拥挤度计算
chromosome = non_domination_sort_mod(chromosome, M, V);
%% 主程序循环
for i = 1 : gen
pool = round(pop/2); %交配池大小
tour = 2; %竞标赛,参赛选手个数
%竞标赛选择适合繁殖的父代
parent_chromosome = tournament_selection(chromosome, pool, tour);
mu = 20;
mum = 20;
offspring_chromosome = genetic_operator(parent_chromosome,M, V, mu, mum, min_range, max_range);
[main_pop,~] = size(chromosome);
[offspring_pop,~] = size(offspring_chromosome);
clear temp
intermediate_chromosome(1:main_pop,:) = chromosome;
intermediate_chromosome(main_pop + 1 : main_pop + offspring_pop,1 : M+V) = offspring_chromosome;
intermediate_chromosome = non_domination_sort_mod(intermediate_chromosome, M, V);
chromosome = replace_chromosome(intermediate_chromosome, M, V, pop);
if ~mod(i,100)
clc;
fprintf('%d generations completed\n',i);
end
end
figure(1);
if M == 2
plot(chromosome(:,V + 1),chromosome(:,V + 2),'*');
xlabel('f_1'); ylabel('f_2');
title('Pareto Optimal Front');
elseif M == 3
plot3(chromosome(:,V + 1),chromosome(:,V + 2),chromosome(:,V + 3),'*');
xlabel('f_1'); ylabel('f_2'); zlabel('f_3');
title('Pareto Optimal Surface');
end
figure(2);
plot(timef,rin,'r',timef,yout,'b');
xlabel('Time(s)');ylabel('rin,yout');
%% //*******子程序initialize_variables**********//
function f = initialize_variables(N, M, V, min_range, max_range)
min = min_range;
max = max_range;
K = M + V;
for i = 1 : N
for j = 1 : V
f(i,j) = min(j) + (max(j) - min(j))*rand(1);
end
Kpidi=f(i,:); %单个可行解
f(i,V + 1: K) = evaluate_objective(Kpidi, M, V);
end
end
%% //*******子程序non_domination_sort_mod**********//
function f = non_domination_sort_mod(x, M, V)
[N, ~] = size(x);
clear m
front = 1;
F(front).f = [];
individual = [];
for i = 1 : N
individual(i).n = 0;
individual(i).p = [];
for j = 1 : N
dom_less = 0;
dom_equal = 0;
dom_more = 0;
for k = 1 : M
if (x(i,V + k) < x(j,V + k))
dom_less = dom_less + 1;
elseif (x(i,V + k) == x(j,V + k))
dom_equal = dom_equal + 1;
else
dom_more = dom_more + 1;
end
end
if dom_less == 0 && dom_equal ~= M
individual(i).n = individual(i).n + 1;
elseif dom_more == 0 && dom_equal ~= M
individual(i).p = [individual(i).p j];
end
end
if individual(i).n == 0
x(i,M + V + 1) = 1;
F(front).f = [F(front).f i];
end
end
while ~isempty(F(front).f)
Q = [];
for i = 1 : length(F(front).f)
if ~isempty(individual(F(front).f(i)).p)
for j = 1 : length(individual(F(front).f(i)).p)
individual(individual(F(front).f(i)).p(j)).n = ...
individual(individual(F(front).f(i)).p(j)).n - 1;
if individual(individual(F(front).f(i)).p(j)).n == 0
x(individual(F(front).f(i)).p(j),M + V + 1) = ...
front + 1;
Q = [Q individual(F(front).f(i)).p(j)];
end
end
end
end
front = front + 1;
F(front).f = Q;
end
[temp,index_of_fronts] = sort(x(:,M + V + 1));
for i = 1 : length(index_of_fronts)
sorted_based_on_front(i,:) = x(index_of_fronts(i),:);
end
current_index = 0;
%% Crowding distance
for front = 1 : (length(F) - 1)
distance = 0;
y = [];
previous_index = current_index + 1;
for i = 1 : length(F(front).f)
y(i,:) = sorted_based_on_front(current_index + i,:);
end
current_index = current_index + i;
sorted_based_on_objective = [];
for i = 1 : M
[sorted_based_on_objective, index_of_objectives] = ...
sort(y(:,V + i));
sorted_based_on_objective = [];
for j = 1 : length(index_of_objectives)
sorted_based_on_objective(j,:) = y(index_of_objectives(j),:);
end
f_max = ...
sorted_based_on_objective(length(index_of_objectives), V + i);
f_min = sorted_based_on_objective(1, V + i);
y(index_of_objectives(length(index_of_objectives)),M + V + 1 + i)...
= Inf;
y(index_of_objectives(1),M + V + 1 + i) = Inf;
for j = 2 : length(index_of_objectives) - 1
next_obj = sorted_based_on_objective(j + 1,V + i);
previous_obj = sorted_based_on_objective(j - 1,V + i);
if (f_max - f_min == 0)
y(index_of_objectives(j),M + V + 1 + i) = Inf;
else
y(index_of_objectives(j),M + V + 1 + i) = ...
(next_obj - previous_obj)/(f_max - f_min);
end
end
end
distance = [];
distance(:,1) = zeros(length(F(front).f),1);
for i = 1 : M
distance(:,1) = distance(:,1) + y(:,M + V + 1 + i);
end
y(:,M + V + 2) = distance;
y = y(:,1 : M + V + 2);
z(previous_index:current_index,:) = y;
end
f = z();
end
%% //*******子程序tournament_selection**********//
function f = tournament_selection(chromosome, pool_size, tour_size)
[pop, variables] = size(chromosome);
rank = variables - 1;
distance = variables;
for i = 1 : pool_size
for j = 1 : tour_size
candidate(j) = round(pop*rand(1));
if candidate(j) == 0
candidate(j) = 1;
end
if j > 1
while ~isempty(find(candidate(1 : j - 1) == candidate(j)))
candidate(j) = round(pop*rand(1));
if candidate(j) == 0
candidate(j) = 1;
end
end
end
end
for j = 1 : tour_size
c_obj_rank(j) = chromosome(candidate(j),rank);
c_obj_distance(j) = chromosome(candidate(j),distance);
end
min_candidate = ...
find(c_obj_rank == min(c_obj_rank));
if length(min_candidate) ~= 1
max_candidate = ...
find(c_obj_distance(min_candidate) == max(c_obj_distance(min_candidate)));
if length(max_candidate) ~= 1
max_candidate = max_candidate(1);
end
f(i,:) = chromosome(candidate(min_candidate(max_candidate)),:);
else
f(i,:) = chromosome(candidate(min_candidate(1)),:);
end
end
end
%% //*******子程序genetic_operator**********//
function f = genetic_operator(parent_chromosome, M, V, mu, mum, l_limit, u_limit)
[N,m] = size(parent_chromosome);
clear m
p = 1;
was_crossover = 0;
was_mutation = 0;
for i = 1 : N
% With 90 % probability perform crossover
if rand(1) < 0.9
% Initialize the children to be null vector.
child_1 = [];
child_2 = [];
% Select the first parent
parent_1 = round(N*rand(1));
if parent_1 < 1
parent_1 = 1;
end
% Select the second parent
parent_2 = round(N*rand(1));
if parent_2 < 1
parent_2 = 1;
end
% Make sure both the parents are not the same.
while isequal(parent_chromosome(parent_1,:),parent_chromosome(parent_2,:))
parent_2 = round(N*rand(1));
if parent_2 < 1
parent_2 = 1;
end
end
% Get the chromosome information for each randomnly selected
% parents
parent_1 = parent_chromosome(parent_1,:);
parent_2 = parent_chromosome(parent_2,:);
% Perform corssover for each decision variable in the chromosome.
for j = 1 : V
% SBX (Simulated Binary Crossover).
% For more information about SBX refer the enclosed pdf file.
% Generate a random number
u(j) = rand(1);
if u(j) <= 0.5
bq(j) = (2*u(j))^(1/(mu+1));
else
bq(j) = (1/(2*(1 - u(j))))^(1/(mu+1));
end
% Generate the jth element of first child
child_1(j) = ...
0.5*(((1 + bq(j))*parent_1(j)) + (1 - bq(j))*parent_2(j));
% Generate the jth element of second child
child_2(j) = ...
0.5*(((1 - bq(j))*parent_1(j)) + (1 + bq(j))*parent_2(j));
% Make sure that the generated element is within the specified
% decision space else set it to the appropriate extrema.
if child_1(j) > u_limit(j)
child_1(j) = u_limit(j);
elseif child_1(j) < l_limit(j)
child_1(j) = l_limit(j);
end
if child_2(j) > u_limit(j)
child_2(j) = u_limit(j);
elseif child_2(j) < l_limit(j)
child_2(j) = l_limit(j);
end
end
child_1(:,V + 1: M + V) = evaluate_objective(child_1, M, V);
child_2(:,V + 1: M + V) = evaluate_objective(child_2, M, V);
was_crossover = 1;
was_mutation = 0;
% With 10 % probability perform mutation. Mutation is based on
% polynomial mutation.
else
% Select at random the parent.
parent_3 = round(N*rand(1));
if parent_3 < 1
parent_3 = 1;
end
% Get the chromosome information for the randomnly selected parent.
child_3 = parent_chromosome(parent_3,:);
% Perform mutation on eact element of the selected parent.
for j = 1 : V
r(j) = rand(1);
if r(j) < 0.5
delta(j) = (2*r(j))^(1/(mum+1)) - 1;
else
delta(j) = 1 - (2*(1 - r(j)))^(1/(mum+1));
end
% Generate the corresponding child element.
child_3(j) = child_3(j) + delta(j);
% Make sure that the generated element is within the decision
% space.
if child_3(j) > u_limit(j)
child_3(j) = u_limit(j);
elseif child_3(j) < l_limit(j)
child_3(j) = l_limit(j);
end
end
child_3(:,V + 1: M + V) = evaluate_objective(child_3, M, V);
% Set the mutation flag
was_mutation = 1;
was_crossover = 0;
end
if was_crossover
child(p,:) = child_1;
child(p+1,:) = child_2;
was_cossover = 0;
p = p + 2;
elseif was_mutation
child(p,:) = child_3(1,1 : M + V);
was_mutation = 0;
p = p + 1;
end
end
f = child;
end
%% //*******子程序replace_chromosome**********//
function f = replace_chromosome(intermediate_chromosome, M, V,pop)
[N, m] = size(intermediate_chromosome);
% Get the index for the population sort based on the rank
[temp,index] = sort(intermediate_chromosome(:,M + V + 1));
clear temp m
% Now sort the individuals based on the index
for i = 1 : N
sorted_chromosome(i,:) = intermediate_chromosome(index(i),:);
end
% Find the maximum rank in the current population
max_rank = max(intermediate_chromosome(:,M + V + 1));
% Start adding each front based on rank and crowing distance until the
% whole population is filled.
previous_index = 0;
for i = 1 : max_rank
% Get the index for current rank i.e the last the last element in the
% sorted_chromosome with rank i.
current_index = max(find(sorted_chromosome(:,M + V + 1) == i));
% Check to see if the population is filled if all the individuals with
% rank i is added to the population.
if current_index > pop
% If so then find the number of individuals with in with current
% rank i.
remaining = pop - previous_index;
% Get information about the individuals in the current rank i.
temp_pop = ...
sorted_chromosome(previous_index + 1 : current_index, :);
% Sort the individuals with rank i in the descending order based on
% the crowding distance.
[temp_sort,temp_sort_index] = ...
sort(temp_pop(:, M + V + 2),'descend');
% Start filling individuals into the population in descending order
% until the population is filled.
for j = 1 : remaining
f(previous_index + j,:) = temp_pop(temp_sort_index(j),:);
end
return;
elseif current_index < pop
% Add all the individuals with rank i into the population.
f(previous_index + 1 : current_index, :) = ...
sorted_chromosome(previous_index + 1 : current_index, :);
else
% Add all the individuals with rank i into the population.
f(previous_index + 1 : current_index, :) = ...
sorted_chromosome(previous_index + 1 : current_index, :);
return;
end
% Get the index for the last added individual.
previous_index = current_index;
end
end
3.3NSGA-2算法的PID参数整定仿真图
图4-8 NSGA-2 算法的适应度函数图
4参考文献
[1]袁雷,胡冰新,魏克银,等.现代永磁同步电机控制原理及MATLAB仿真[M].北京:北京航空航天大学出版社,2016(03):12-18.
[2]Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.
[3]Zhang Q, Li H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6):712-731.
[4]M. Andersson, S. Bandaru and A. H. C. Ng, “Towards optimal algorithmic parameters for simulation-based multi-objective optimization,” 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, 2016, pp. 5162-5169.